Собственная проводимостЬ полупроводника

Полупроводник при имеетзону проводимости свободную от электронов и полностью заполненную валентную зону, отделенную запрещенной зоной шириной . В валентной зоне отсутствуют свободные места, куда могли бы переместиться заряды, в зоне проводимости зарядов нет. В результате полупроводник является изолятором.

При тепловое движение перебрасывает электроны через запрещенную зону, в зоне проводимости появляются электроны, в валентной зоне – вакантные места –дырки.

При термодинамическом равновесии химические потенциалы электронов и дырок равны. Энергию отсчитываем от края валентной зоны.

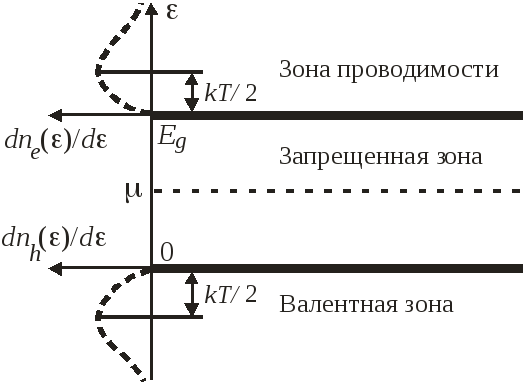
Зона проводимости . Кинетическая энергия электрона

.

Плотность состояний (3.8) единицы объема трехмерного газа

.

Концентрация электронов n_e мала, газ невырожденный, используем распределение Максвелла

.

Из

,

находим число электронов в единице объема с энергией в интервале

. (П.10.4)

Концентрация электронов со всеми энергиями

.

В интеграле заменяем аргумент и интегрируем

,

где использована формула

.

Получаем концентрацию электронов в зоне проводимости

, (П.10.5)

где

.

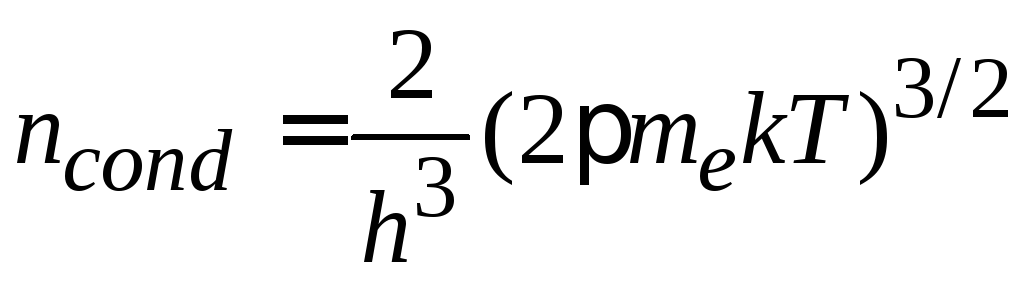Для Si при :

эВ, , см^–3.

Эффективную массу электрона выражаем через концентрацию электроновпри помощи (П.10.5)

.

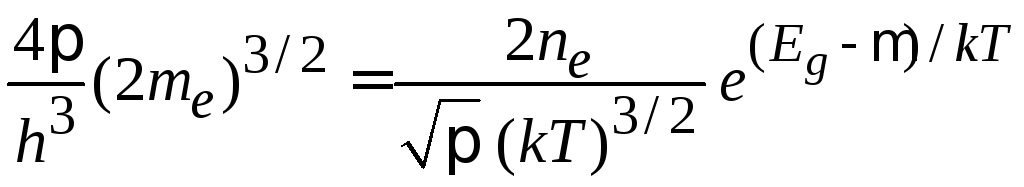Подставляем в (П.10.4)

и находим число электронов в единичном интервале энергии зоны проводимости

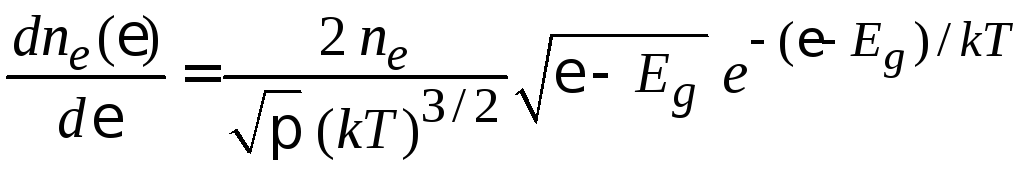. (П.10.4а)

Результат совпадает с распределением Максвелла по энергии. График показан пунктиром на рисунке.

Валентная зона  < 0,

.

Плотность состояний (3.8) дырок h (от англ. hole – «дырка»)

.

Дырка – это не заполненное электроном состояние валентного уровня, поэтому в валентной зоне среднее число электронов и дырок в одном состоянии

.

Из распределения Ферми–Дирака для электронов

получаем распределение Ферми–Дирака для дырок

.

Сравнение распределений ипоказывает, чтохимические потенциалы электронов и дырок противоположны по знаку. Концентрация дырок мала, газ невырожденный, пренебрегаем единицей в знаменателе, получаем распределение Максвелла для дырок

.

В результате

. (П.10.6)

Интегрируем по энергии валентной зоны

.

Заменяем

,

получаем концентрацию дырок в валентной зоне

, (П.10.7)

где

.

Эффективную массу дырки выражаем через концентрацию дырок при помощи (П.10.7)

.

Подставляем в (П.10.6) и находим число дырок в единичном интервале энергии валентной зоны

. (П.10.6а)

График распределения показан пунктиром на рисунке.

Электронейтральность полупроводника означает, что концентрация электронов в зоне проводимости равна концентрации дырок в валентной зоне. Из (П.10.5) и (П.10.7) находим

. (П.10.8)

Концентрация носителей тока увеличивается с ростом температуры и с уменьшением ширины запрещенной зоны.

Из с учетом (П.10.5) и (П.10.7) получаем

.

Выражаем химический потенциал

. (П.10.9)

При Т  0

.

Следовательно, уровень химического потенциала:

• расположен в середине запрещенной зоны при низкой температуре;

• чем выше температура, тем сильнее уровень приближается к той зоне, где масса частиц и плотность состояний меньше;

• расположен в середине запрещенной зоны при любой температуре при равенстве эффективных масс электронов и дырок.