Распределение Бозе–Эйнштейна

Среднее число бозонов в одном состоянии. Для бозонов допустимо любое число частиц в одном состоянии

.

Из (4.5а)

получаем

.

Сумма является геометрической прогрессией. Она сходится, если основание прогрессии , тогда. Учитывая, получаем, чтохимический потенциал бозонов не может быть положительным

. (4.9)

Суммируем геометрическую прогрессию

,

получаем статистическую сумму

,

.

Подставляем в (4.7)

,

находим

.

Получаем среднее число бозонов в состоянии с энергией  – распределение Бозе–Эйнштейна

. (4.10)

Условие

обеспечивает при любой энергии и температуре. С ростом температуры химический потенциал бозонов медленно уменьшается, а его модуль увеличивается. Принаходим

. (4.11)

Чем больше , тем меньшеB. В нефизической области при из (4.10) получаем.

Распределение бозонов по энергии при

Распределения частиц в классических и квантовых системах

Распределение классических частиц по энергии является распределением Максвелла. Используем выражение числа частиц в единичном интервале энергии (2.62в) через химический потенциал

.

Учитываем плотность состояний частицы трехмерного газа (3.8а)

.

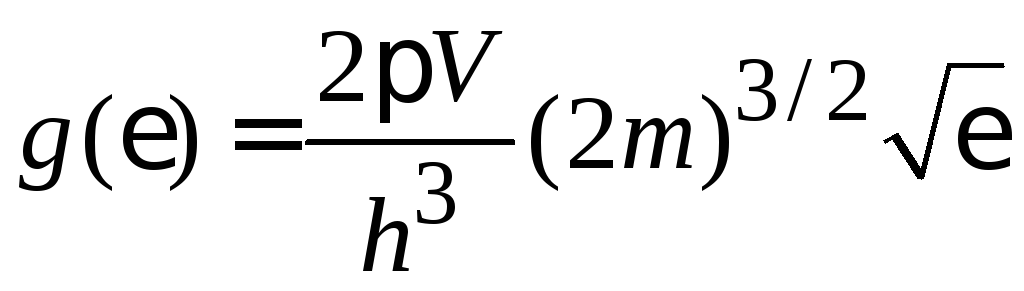Получаем среднее число частиц в состоянии с энергией  – распределение Максвелла–Больцмана

. (4.12)

Объединенное распределение имеет вид

, (4.13)

где

Распределения Максвелла (М),

Бозе–Эйнштейна (Б), Ферми–Дирака (Ф)

Квантовые распределения (4.8) и (4.10) переходят в классическое распределение (4.12) при

.

Тогда из

находим

, при .

Используя активность

,

для классической системы получаем

, ,

. (4.14)

Химический потенциал входит в функцию распределения. Если частица имеет сохраняющийся заряд – электрический, и/или барионный, и/или лептонный, то в изолированной системе число частиц сохраняется, и химический потенциал определяется из условия нормировки распределения на число частиц системы. Число частиц в интервале энергии

интегрируем, и получаем число частиц системы:

, (4.15)

где n – концентрация частиц.

Для трехмерной частицы с законом дисперсии плотность состояний (3.8а)

, .

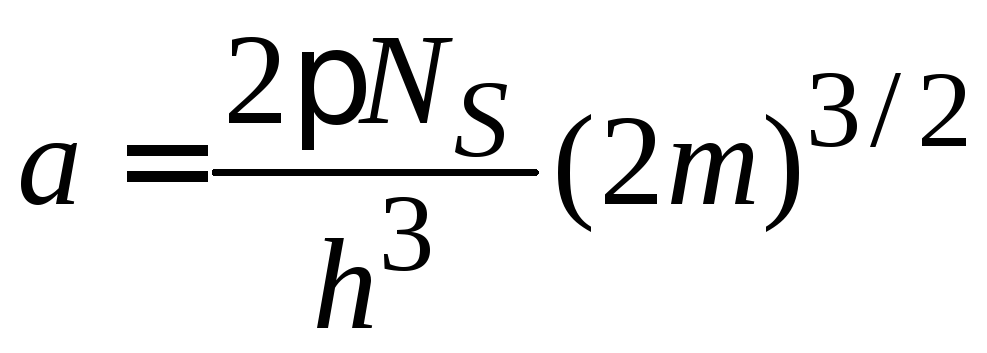Для распределения (4.13)

,

получаем концентрацию частиц

. (4.16)

Следовательно, химический потенциал зависит от массы частицы m, от числа спиновых состояний N_S, от концентрации n, от температуры T и от рода газа .

Критическая температура фермионов. Химический потенциал трехмерного газа фермионов меняет знак при повышении температуры, как показано на рисунке.

Химический потенциал фермионов

Определяем критическую температуру фермионов условием

.

Виды фермионного газа. В зависимости от температуры газа различают:

–невырожденный газ, близкий к классическому газу;

–вырожденный газ с квантовыми свойствами.

Невырожденный газ описывается распределением Максвелла. Из (4.16)

при получаем концентрацию газа

,

где использовано

, .

Откуда выражаем активность и химический потенциал

,

. (4.17)

Химический потенциал невырожденного трехмерного газа отрицательный, уменьшается с повышением температуры и увеличивается с ростом концентрации частиц. При результат совпадает с химическим потенциалом (2.62а) классического газа. Условия применимости классического распределения (4.14)

,

(4.18)

выполняются, если:

• масса частицы m – велика;

• концентрация частиц n – мала;

• температура T – велика.

Вырожденный газ фермионов проявляет квантовые свойства и нарушает условия (4.18), тогда активность и химический потенциал достаточно большие

, .

Условия применимости квантового распределения:

• масса частицы мала;

• концентрация частиц велика;

• температура не превышает критического значения ;

• ширина переходной области вблизи уровня Ферми мала по сравнению с энергией Ферми, тепловая энергия возбуждает незначительное количество из общего числа частиц.

Критическая температура фермионов. Используем

.

Из (4.16)

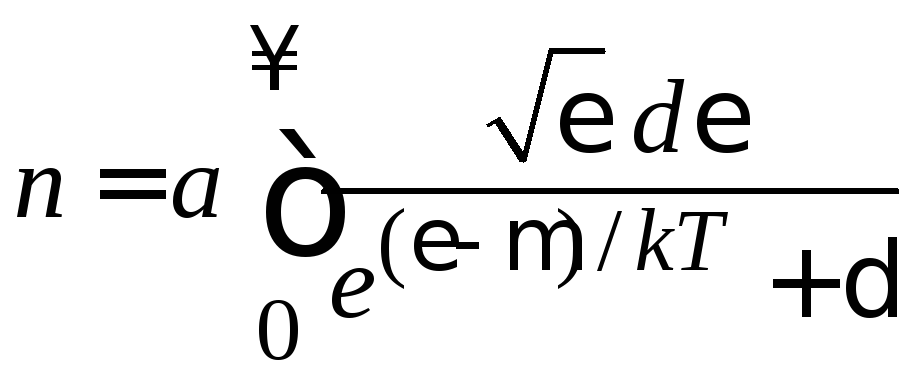
при , получаем

.

Интеграл равен

,

где использовано

,

тогда

. (4.19)

Для электронов ,

. (4.19а)

Физический смысл критической температуры. Согласно распределению Максвелла наиболее вероятная скорость частицы

.

При ей соответствует длина волны де Бройля

,

где учтено (4.19а). Концентрацию частиц выражаем через среднее расстояние d между частицами

, .

Из получаем

.

При критической температуре длина волны де Бройля сравнима со средним расстоянием между частицами.

Для квантового газа фермионов:

• длина волны де Бройля сопоставима, или больше, расстояния между частицами ;

• температура газа сравнима, или ниже, критической температуры ;

• ширина переходной области мала по сравнению с энергией Ферми;

• тепловое движение активизирует малое число электронов, находящихся вблизи уровня Ферми.

Для классического газа фермионов:

• длина волны де Бройля мала ;

• температура газа высокая ;

• ширина переходной области велика и сопоставима с максимальной энергией фермионов;

• все электроны активизированы тепловым движением;

• наиболее вероятный импульс большой.

Для электронного газа в металле

n  (1–18)10²² см^–3, m  10^–27 г.

Из (4.19а)

находим

К.

При нормальной температуре получаем и газ вырожден, доля активизированных электронов не превышает 1%. Это объясняет противоречие между классической теорией теплоемкости и экспериментом, показавшим, что электронный газ не дает вклада в теплоемкость металла.

Для собственного полупроводника

n  10¹⁷ см^–3, К.

При нормальной температуре , газ не вырожден, выполняется распределение Максвелла.

Молекулярный газ, например гелий с m » 3700m_эл, остается невырожденным до очень низких температур.

Тепловые флуктуации числа частиц описывает дисперсия (П.7.3)

.

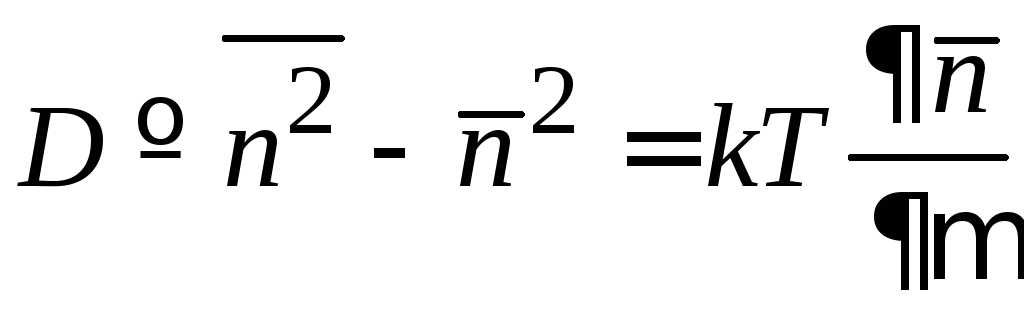Для универсального распределения (4.13)

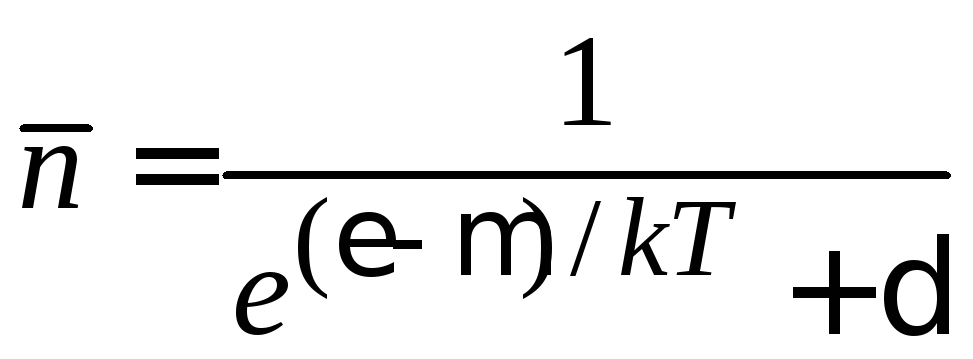
получаем

.

В результате

. (4.20)

Для фермионов ,

.

При 0 и1 получаем, на уровне ФермииD_max = 0,25.Флуктуация фермионов не велика и максимальна на уровне Ферми.

Для бозонов ,

.

При большой заселенности уровня дисперсия велика

.

Это объясняется взаимной интерференцией волновых пакетов, представляющих отдельные частицы и следующих в случайной последовательности. При интерференции двух волн с равными амплитудами наибольшая амплитуда удваивается, а интенсивность волны и плотность вероятности учетверяются. Наименьшая амплитуда и плотность вероятности равны нулю. В результате дисперсия числа частиц увеличивается. Интерференцией объясняется взаимное «притяжение» бозонов – при тепловом равновесии бозоны перемещаются группами. Фотонные пары с меньшим временным интервалом регистрируются чаще, чем пары с большим интервалом. Вероятность найти тождественные бозоны в близких квантовых состояниях выше, чем вероятность найти нетождественные частицы.

У фермионов перекрытие когерентных пакетов запрещено принципом Паули. Это приводит к взаимному «отталкиванию» фермионов и уменьшает флуктуацию числа частиц.

Эти выводы подтверждает эксперимент T. Jeltes at al. Comparison of the Hanbury Brown–Twiss effect for bosons and fermions // Nature 445, 402 (2007), с атомами бозонами ⁴He и атомами фермионами ³He, которые при температуре К распространялись в виде облачка от магнитных ловушек и регистрировались детекторами, отстоящими друг от друга на расстояние вдоль направления движения. Измеряласькорреляционная функция , равная вероятности одновременной регистрации частиц двумя детекторами, деленная на произведение вероятностей регистрации частиц каждым детектором по отдельности. При отсутствии корреляции приход частиц случаен и из теоремы о произведении вероятностей независимых событий получаем. Корреляционная функции, показанные на рисунке, свидетельствуют огруппировке бозонов и антигруппировке фермионов при расстояниях между частицами <1 мм. Аналогичная зависимость получена в поперечном к пучку направлении. Корреляция возникает при перекрытии волновых функций частиц и вызвана их симметрией при взаимной перестановке частиц. Результаты описывает функция

.

Зависимость от расстояния между детекторами

корреляционной функции бозонови фермионов

При температуре газа Т  0,5 мкК параметр контрастностности , корреляционная длина ,мм,мм, где λ иp – длина волны и импульс частицы. Параметры η и l увеличиваются при понижении температуры.

Корпускулярно-волновой дуализм бозонов. Согласно (4.20) для бозонов дисперсия

является суммой двух слагаемых. Из теории вероятностей известно, что в случае действия на систему независимых случайных факторов, вызванные ими дисперсии складываются. Линейное слагаемое дисперсии бозонов соответствует флуктуации, вызванной дробовым шумом частиц. Квадратичное слагаемое соответствует флуктуации, вызванной шумом интерферирующих волн. Наличие двух вкладов в дисперсию фотонов обнаружил Эйнштейн в 1909 г. Он рассматривал этот факт как проявление корпускулярно-волнового дуализма, т. е. совмещения волновых и корпускулярных свойств у квантового объекта.

При малой энергии, низкой частоте, большой длине волны заселенность состояний бозонов велика , тогда главный вклад дает. Следовательно, система проявляет волновые свойства, в объеме газа распределено поле, а не частицы.

При большой энергии, большой частоте, малой длине волны заселенность мала , тогда главный вклад дает. Следовательно, система проявляет корпускулярные свойства, в объеме газа распределены частицы.Для классического идеального газа , дисперсия мала.Флуктуация является дробовым шумом, газ проявляет корпускулярные свойства, и ведет себя как множество частиц.