Статистические распределения фермионов и бозонов

Идеальный газ фермионов или бозонов находится в фиксированном объеме, т. е. в потенциальной яме, при температуре Т. Частица в яме имеет дискретный энергетический спектр. Частицы газа обмениваются энергией и переходят между уровнями, число частиц в каждом энергетическом состоянии системы изменяется. Поэтому система описывается большим каноническим распределением. Откуда получаем среднее число частиц в одном состоянии на уровне энергии ε.

Фермионы имеют полуцелый спин и подчиняются принципу Паули – в одном квантовом состоянии не может быть более одной частицы. Среднее число частиц в одном состоянии описывается распределением Ферми–Дирака, которое получили Энрико Ферми в 1925 г. и Поль Дирак в 1926 г.

Бозоны обладают целочисленным спином, не имеют ограничения на число частиц в одном состоянии, и описываются распределением Бозе–Эйнштейна. Распределение для фотонов со спином получил Шатьендранат Бозе в 1924 г. Обобщение на случай частиц с произвольным целым спином дал Альберт Эйнштейн в 1925 г.

Элементарные частицы фермионы и бозоны выполняют в природе разные функции. Фермионы в виде электронов, нуклонов, кварков образуют материю, из которой состоят тела. Бозоны в виде фотонов, фононов, глюонов, и-бозонов в виртуальном состоянии являются переносчиками взаимодействий между частицами материи. Составные частицы материи – атомы и молекулы могут быть фермионами или бозонами.

Большое каноническое распределение квантовой системы

Идеальный газ при фиксированных T и V, обменивающийся энергией и частицами с термостатом, описывается большим каноническим распределением. Получим среднее число частиц на произвольном энергетическом уровне в многоуровневой системе.

Состояние i многоуровневой системы. Каждая частица ограниченной в пространстве стационарной квантовой системы имеет дискретный спектр энергии

Спектр описывается плотностью состояний. Частное распределение частиц по уровням энергии образует состояние системы

,

где – число частиц на уровне. Полная энергия и число частиц в состоянииi

, . (4.1)

Вероятность состояния i. Используем большое каноническое распределение классической системы. Оно дает вероятность того, что система имеет N частиц и находится в единице объема фазового пространства около точки X

.

Для квантовой системы распределение имеет аналогичный вид согласно принципу соответствия. Тогда дискретное состояние i реализуется с вероятностью

, (4.2)

где – химический потенциал равновесной системы.Подставляем (4.1) в (4.2)

, (4.2а)

где учтено свойство экспоненты.

Распределения частиц по уровням энергии. Статистически независимые уровни энергии рассматриваем как подсистемы. По теореме умножения вероятностей независимых событий вероятность состояния системы равно произведению вероятностей состояний ее независимых подсистем

.

Сравниваем с (4.2а), и получаем вероятность нахождения частиц на уровнеk с энергией

, (4.3)

. (4.4)

Учтено, что для равновесной системы химический потенциал одинаков у всех подсистем.

Статистическая сумма подсистемы с энергией находим из нормировки вероятности

.

Подстановка (4.3) дает

. (4.5)

Для частиц в макроскопическом объеме спектр энергии квазинепрерывный . В (4.3) и (4.5) заменяем и получаем вероятность нахождения n частиц в состоянии с энергией и статистическую сумму

,

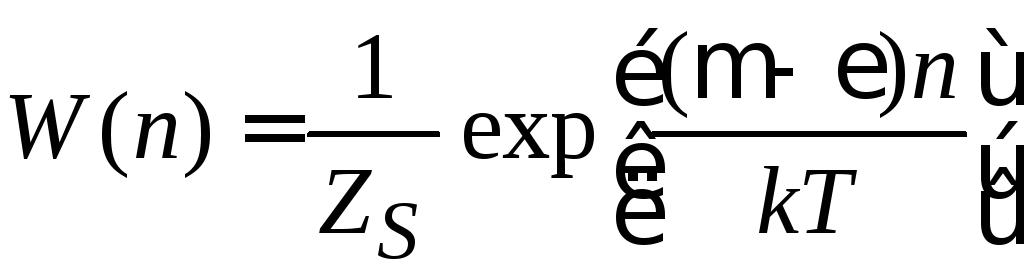. (4.5а)

Среднее число частиц в состоянии с энергией без учета вырождения по спину, которое учитывается плотностью состояний, находим из определения среднего и (4.5а)

. (4.6)