Примеры

1. Найти состояния электрона в прямоугольной симметричной потенциальной яме шириной 2а с абсолютно непроницаемыми стенками Яма моделирует находящийся в вакууме кусок металла размером 2a с работой выхода, существенно превышающей энергию свободного электрона.

Разбиваем ось x на участки 1, 2, 3. В областях 1 и 3 при потенциальная энергия бесконечная, выполняется условие (3.14) . Следовательно, за пределами ямы и на стенках

, .

В области 2 внутри ямы при уравнение Шредингера (3.2) имеет вид

,

где

, .

Яма симметричная, используем вещественные нечетное (1) и четное (2) решения

, .

Граничные условия при дают узлы волновой функции

,

.

Четные состояния. Граничное условие требует

.

Получаем дискретный набор решений ,

,

в общем виде

,

Тогда

,

.

Постоянную с находим из условия ортонормированности дискретного спектра

.

С учетом

,

с точностью до постоянной фазы получаем ,

. (П.3.1)

Основное состояние

, .

Нечетные состояния. Граничное условие

дает набор решений

,

в общем виде

,

Тогда

,

.

Ортонормированность

дает ,

. (П.3.2)

Первое возбужденное состояние

, .

Объединяем результаты для четных и нечетных состояний, получаем спектр энергии

, , (П.3.3)

где n – число узлов волновой функции на протяжении ямы. Энергии четных и нечетных состояний чередуются. Расстояние между соседними уровнями увеличивается с ростом n как 2n +1. При сужении ямы уровни поднимаются.

Функции состояний образуют ортонормированный базис

, (П.3.4)

2. Найти связанные состояния в прямоугольной яме глубиной W, шириной .

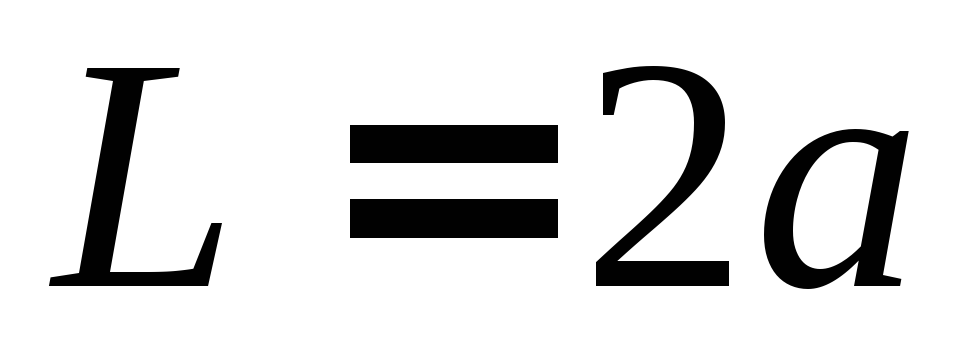Такую яму создает гетероструктура . Слойимеет более узкую запрещенную зону по сравнению с соседними слоями. В зоне проводимостиобразуется прямоугольная потенциальная яма глубиной, шириной, равной толщине слоя. На дне зоны проводимостиэффективная масса электрона.

На оси x выделяем участки 1, 2 и 3. Внутри ямы в области 2 при учитываем. Ищем связанные состояния. Используем стационарное уравнение Шредингера (3.2)

,

. (П.3.6)

Яма симметричная, выделяем четное и нечетное решения

,

. (П.3.7)

Вне ямы в областях 1 и 3 при учитываем, уравнение Шредингера (3.1)

получает вид

,

. (П.3.8)

Используем убывающие с удалением от ямы решения

, . (П.3.9)

Параметры

,

связаны соотношением

, (П.3.10)

где борновский параметр

не зависит от E.

Сшиваем решения (П.3.7) и (П.3.9) при , используя (3.11) и (3.12)

,

.

Для четного решения сшиваем

, ,

находим

,

.

Взаимным делением избавляемся от постоянных с и . Получаем

. (П.3.11)

Для нечетного решения сшиваем

, ,

аналогично получаем

,

,

тогда

. (П.3.12)

Для нахождения параметров k и ξ для четных состояний используем систему уравнений (П.3.10) и (П.3.11)

,

.

Для нечетных состояний используем (П.3.10) и (П.3.12)

,

.

Уравнения трансцендентные, для решения применяем графический метод. Безразмерные рассматриваем как декартовые координаты. Уравнение описывает окружность радиусом

,

который известен из данных задачи. На рисунке последовательность дуг 1, 2, 3, 4 соответствует росту глубины ямы W. Функции ипериодические, каждой ветвисоответствует своя кривая. Уравнение четных состояний

для ветвей соответствует пунктирным кривым. Уравнение нечетных состояний

при дает сплошную кривую.

Точка пересечения окружности с кривой, спроектированная на оси координат, дает и, и уровень энергии

.

При малой глубине ямы W окружность радиусом (на рис. дуга 1) всегда пересекает кривую. Следовательно,в одномерной яме сколь угодно малой глубины существует связанное основное состояние , удовлетворяющее

, ,

тогда из получаем , где– энергия основного состояния в бесконечно глубокой яме шириной 2a. Энергия основного состояния Е₀ в яме конечной глубины меньше энергии основного состояния в бесконечно глубокой яме.

С увеличением глубины ямы растет радиус дуги , тогда согласно рисунку возрастаети энергия основного состояния. При,появляется следующий уровень си энергиейу верха ямы. При дальнейшем увеличенииW возрастают и, но медленнее, чемW. В интервале

,

существуют два состояния – основное и первое возбужденное. Они показаны на рисунке.

3. Найти связанные состояния в дельта-образной яме , где– безразмерный параметр, определяющий силу ямы;d имеет размерность длины. Пример моделирует квантовую точку с низким уровнем энергии незаполненного состояния.

Для связанного состояния с из (3.1)

получаем

,

, .

При для уравнения

используем убывающие решения

,

.

Сшиваем их при , используя (3.11) и (3.13):

, ,

,

где

, .

Находим

,

,

тогда

,

,

. (П.3.15)

Существует лишь одно связанное состояние. Условие нормировки

дает

,

в результате

. (П.3.16)

Функция уменьшается в е раз при . Чем больше сила ямы β, тем выше уровень энергии ибыстрее убывает при удалении от ямы.

4. Найти уровни энергии в треугольной яме с линейной зависимостью потенциала. Пример моделирует однородное электрическое полеплоского конденсатора с обкладками перпендикулярными осиx. Внутри конденсатора находится заряд q, на него действует сила .

Пространственное ограничение частицы приводит к дискретности ее спектра энергии. Частица с полной энергией имеет кинетическую энергию

, .

На границе классического движения частица останавливается,

.

Координата точки остановки

.

В уравнении Шредингера (3.1)

, ,

переходим к безразмерному аргументу z, который отсчитываем от точки остановки:

,

тогда

Параметр γ с размерностью длины выбираем исходя из условия

.

Из последнего равенства находим

.

После замены

, ,

уравнение Шредингера становится уравнением Эйри

.

Решение имеет вид интеграла Эйри

. (П.3.27)

Спектр энергии получаем из краевого условия (3.14) для непроницаемой стенки при ,в виде

.

Подставляем (П.3.27) и получаем

.

Используем корни функции Эйри :

, ,,,, ...,

находим спектр энергии

. (П.3.28)

С ростом n расстояние между соседними уровнями медленно уменьшается. Энергия основного состояния

.

Графики волновых функций показаны на рисунке.