Рассеяние на двух локальных барьерах

Частица с волновым числом k проходит через барьеры 1 и 2, сосредоточенные при и. Такое устройство в оптике называетсярезонатор Фабри–Перро. Амплитуду прохождения системы барьеров t требуется выразить через амплитуды прохождения ,и отражения,каждого из барьеров по отдельности. Считать, чторассеяние когерентное, то есть отсутствует хаотический сбой фазы при распространении частицы. Рассмотреть некогерентное рассеяние с хаотическим сбоем фазы.

Когерентное рассеяние. Используем амплитуды бегущих волн около барьера. Фиксируем величину падающих волни, тогда для локальных барьеров

, ,

, .

Для системы барьеров

,

где учтен набег фазы при перемещении волны между входом и выходом.

Падающая волна в промежутке между барьерами складывается из волныи волны, отразившейся от барьера 1, тогда

,

где учены изменения фаз волн на пути между барьерами и амплитуда отражения волныот барьера 1. Из последнего уравнения находим

и получаем

,

где амплитуда прохождения системы барьеров

. (П.4.4)

Для комплексного числа выполняется соотношение

.

Сравнивая с (П.4.4), полагаем

, ,,

находим коэффициент прохождения системы барьеров

, (П.4.4а)

где

; ;

;

; .

Симметричная система барьеров соответствует

,

.

Из (П.4.4а) получаем

. (П.4.4б)

Если энергия частицы удовлетворяет условию резонанса

, , (П.4.4в)

то ,,исистема барьеров не отражает частицу при любом . Волны, отраженные от двух барьеров, при сложении интерферируют и гасят друг друга.

Некогерентное рассеяние сопровождается потерей информации о фазе волн. Коэффициент прохождения получаем путем усреднения хаотических изменений фазы θ

.

Для двух барьеров подстановка (П.4.4а)

с учетом

дает

, ,

.

Для N барьеров по индукции

. (П.4.4г)

Результат аналогичен формуле последовательного соединения резисторов, где соответствует омическому сопротивлению.

Для одинаковых барьеров с коэффициентом прохождения ,из (П.4.4г) с учетомнаходим

. (П.4.4д)

При получаем–коэффициент некогерентного прохождения системы одинаковых барьеров обратно пропорционален их числу, что качественно отличается от результата для резонансного когерентного прохождения. Этот результат используется для экспериментальной проверки степени когерентности системы.

Рассеяние на прямоугольном барьере

Найдем коэффициент прохождения барьера частицей с энергией. Получим условие отсутствия отражения. Рассмотрим туннельный эффект при, и перевернутый барьер. Система реализуется на практике при контакте двух металлов, разделенных диэлектриком или полупроводником.

Стандартное решение. Выделяем области 1, 2 и 3. Из уравнения Шредингера

,

получаем

, ,

, ,

с неизвестными r, t, a, b. Используем условия сшивания при и

, ,

, .

Получаем систему алгебраических уравнений

,

,

,

Решив их и вычислив t, найдем

.

Вычисления громоздкие. Рассмотрим другой метод решения.

Решение на основе системы барьеров. Прямоугольный барьер рассматриваем как систему из двух локальных ступенчатых барьеров со своими амплитудами прохождения и отражения.

Для левого барьера используем (П.4.2) для амплитуды прохождения при падении слева и амплитуды отражения при падении справа

, .

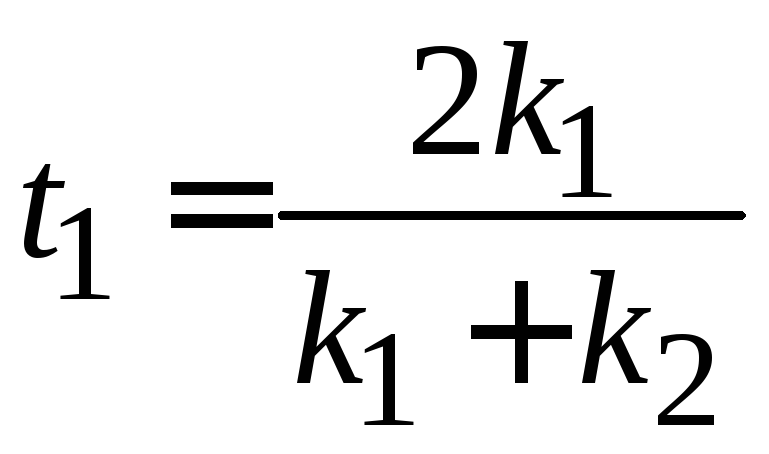При падения слева на правый барьер из (П.4.3) находим

, .

Для системы локальных барьеров, находящихся на расстоянии a друг от друга, выполняется (П.4.4)

.

Подстановка дает амплитуду прохождения системы барьеров

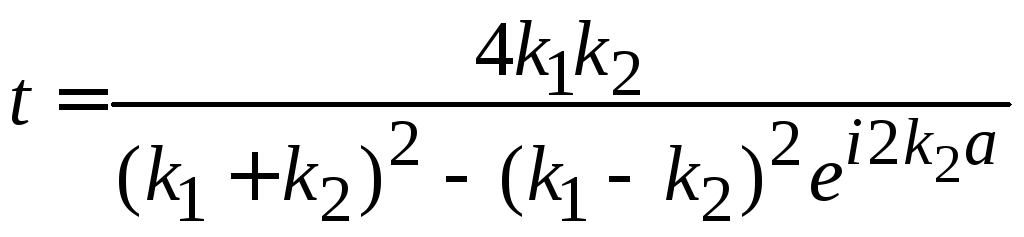. (П.4.5)

Для вычисления коэффициента прохождения используем соотношение

с вещественными

, , , .

Находим коэффициент прохождения системы барьеров

. (П.4.6)

Введенные параметры ε и ν в единицах нм^–2 описывают энергию частицы и высоту барьера, выраженные в электрон-вольтах:

ε(нм^–2)(эВ);

ν(нм^–2)(эВ).

При энергия частицы равна высоте барьера, и из (П.4.6) получаем

. (П.4.6а)

На рисунке показана зависимость коэффициента прохождения от энергии частицы для барьера шириной 5 нм, высотой 1,51 эВ.

Частные случаи:

При ,имеем–туннельный эффект.

При эВ,эВ,эВ, ... функция синуса равна нулю, получаем–резонансное прохождение без отражения.

Резонансное прохождение. Частица с энергией не отражается при

.

Из (П.4.6)

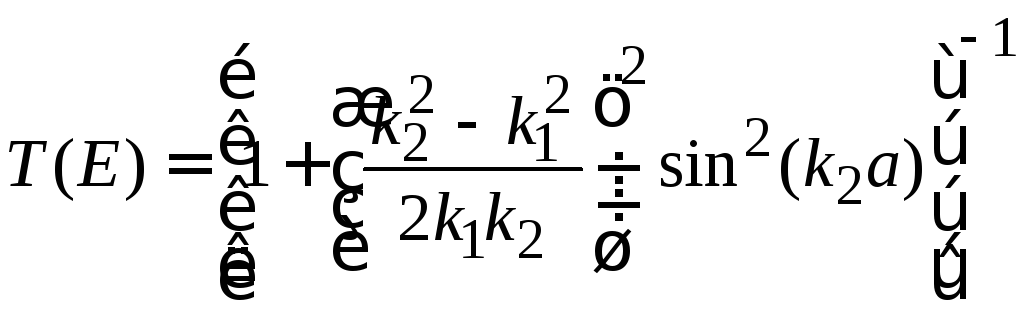
получаем

,

тогда

, ,

,

длина волны де Бройля удовлетворяет условию

. (П.4.6б)

При резонансном прохождении через барьер внутри него укладывается целое число полуволн и возникает квазисвязанное состояние с энергией

.

Падающая волна проходит барьер и набирает ход , часть волны в результате двух отражений проходит путь три раза и набирает ход. Волны интерферируют между собой с разностью хода. Если длина волны де Бройля электрона удовлетворяет условию максимума интерференции , где , то выполняется (П.4.6б), и выходящие из барьера волны усиливаются. Внутри барьера образуется квазисвязанное состояние и частица там задерживается. Она делает неограниченное число попыток пройти барьер и достигается . В оптике прохождение барьера без ослабления света называется просветлением оптики.

Туннельный эффект. Рассмотрим случай .

Уравнение Шредингера для областей 1, 2, 3 дает

, ,

,

;

, ,

.

Для коэффициента прохождения используем (П.4.6)

.

Сравниваем

, ,

получаем

.

Учитываем

,

где использовано

, .

Находим

, (П.4.7)

где

ε(нм^–2)(эВ);

ν(нм^–2)(эВ).

Для сильного барьера

с учетом

из (П.4.7) получаем

. (П.4.8)

Выражение (П.4.8) согласуется с квазиклассическим результатом (3.73а)

с точностью до постоянного множителя перед экспонентой.

Рассеяние на прямоугольной яме.

Яма соответствует перевернутому барьеру. Частица не связана ямой, но она рассеивается, проходя яму. Используем (П.4.6), заменяем , получаем коэффициент прохождения

.

Резонансное прохождение без отражения возникает при

,