Быстрота Изменения величины

Среднее значение физической величины изменяется со временем по следующим причинам:

1. из-за зависимости оператора величины от времени;

2. из-за некоммутативности оператора величины с гамильтонианом.

Оператор производной по времени. Среднее значение величины (2.28)

изменяется с быстротой

.

Используем уравнение Шредингера (2.54)

,

,

получаем

.

Гамильтониан эрмитовый, тогда первое слагаемое в квадратных скобках равно . Объединяем его с третьим слагаемым

. (2.66)

Выражение в круглой скобке по определению является оператором производной по времени

. (2.67)

Слагаемые в правой стороне (2.67) описывают причины, вызывающие изменение физической величины A с течением времени – зависимость от времени и некоммутативностьс гамильтонианом.

Оператор проекции скорости. В (2.67) подставляем , получаем

. (2.67а)

Используем

,

,

находим

.

На практическом занятии доказывается

,

в результате

. (2.67б)

Оператор скорости связан с оператором импульса классическим соотношением, что подтверждает правило соответствия.

Сохраняющаяся величина описывается оператором , удовлетворяющим согласно (2.67) условию

.

Если оператор не зависит от времени , тогда

. (2.68)

Величина сохраняется в любом состоянии, если ее оператор не зависит от времени и коммутирует с гамильтонианом.

Стационарное состояние Ψ для величины a, описываемой оператором , не зависящим от времени, характеризуется тем, что в этом состоянии среднее значениеa постоянно

.

Если , то с учетом (2.66)

получаем условие на Ψ

. (2.69)

Величина а стационарна в состоянии , если среднее значение коммутатора оператора с гамильтонианом равно нулю. В этом случае оператор преобразует состояниев ортогональное к нему состояние.

Ток вероятности

Плотность вероятности обнаружения частицы около точки r

зависит от времени. Вероятность обнаружить частицу во всем пространстве неизменна

.

Следовательно, вероятность перетекает из одного места в другое.

Вводим плотность тока вероятности по аналогии с плотностью электрического тока, полагая для частицы с зарядомe

.

Плотность электрического тока, создаваемая множеством частиц с концентрацией n, движущихся со скоростью v, равна

,

где – заряд, проходящий за 1с через единичное поперечное сечение проводника. Тогда плотность тока вероятности для одной частицы выражается через ее скорость и плотность вероятности

. (2.70)

Плотность тока вероятности и волновая функция. Используем оператор скорости (2.67б)

, (2.70а)

где

.

С учетом (2.70) и (2.70а) определяем плотность тока вероятности для частицы в состоянии

, (2.71)

где использовано

.

Вектор выражаем через декартовые компоненты

,

тогда проекция плотности тока вероятности

. (2.72)

Уравнение непрерывности тока вероятности отражает закон сохранения суммарной вероятности с течением времени. Используем плотность вероятности

,

,

и уравнение Шредингера (2.54)

,

.

Получаем

.

С учетом (2.72)

в выражении первая круглая скобка

и аналогично для остальных скобок. В результате получаем уравнение непрерывности тока вероятности

. (2.73)

Поскольку дивергенция плотности тока divj является потоком из единичного объема, тогда согласно (2.73) поток из объема уменьшает вероятность в этом объеме. Следовательно, уравнение Шредингера описывает систему, у которой нет источников и стоков частиц.

Ток вероятности для частицы с импульсом р. Такое состояние описывается плоской волной

.

Плотность вероятности

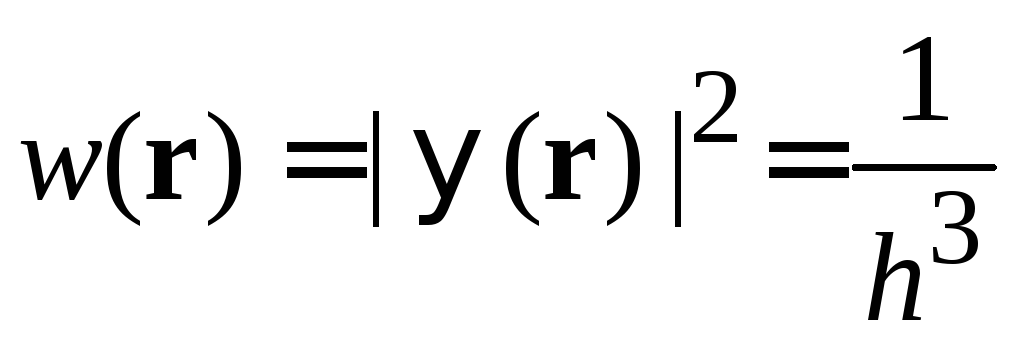
распределена по всему пространству равномерно. В состоянии равномерного движения частица обнаруживается в любой точке пространства с равной вероятностью.

Плотность тока вероятности (2.72)

с учетом

, ,

,

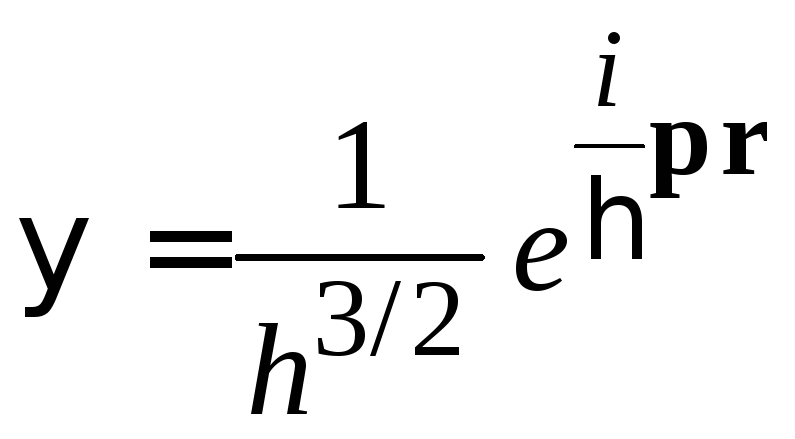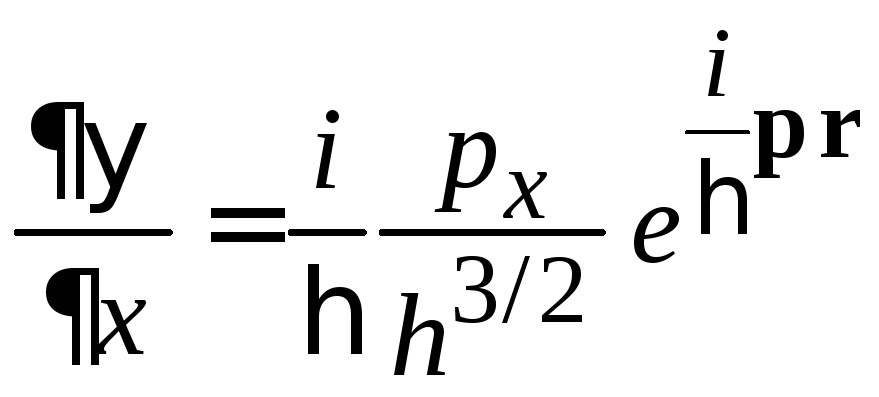равна

,

тогда

.

Результат согласуется с (2.70) .

Плотность электрического заряда и тока для частицы с зарядом е равны

,

.

При равномерном движении заряда используем и получаем известное соотношение для плотности электрического тока

.

Уравнение непрерывности (2.73) для вероятности

умножаем на заряд частицы и получаем закон сохранения заряда в дифференциальной форме

.

Ток вероятности в стационарном состоянии. Стационарное состояние описывается волной (2.63)

с вещественными амплитудой A и фазой φ. Плотность вероятности определяется амплитудой волны

.

Для плотности тока вероятности (2.71)

с учетом

,

получаем

.

Используем

, ,

находим

,

,

, . (2.74)

Для стационарного состояния волновой вектор k равен градиенту фазы волновой функции, плотность тока вероятности j пропорциональна плотности вероятности и градиенту фазы волновой функции. Если фаза  в разных точках одинаковая, то ,.

Согласно (2.73) выполняется

.

В стационарном состоянии поток вероятности из любого объема равен нулю.