
- •Специальные главы физики
- •Практическая значимость курса
- •Рейтинговая аттестация Определение числа баллов
- •Статистическая физика Основные понятия и положения
- •Основы теории вероятностей Вероятность случайного события
- •Характеристики случайной дискретной величины Среднее значение случайной величины
- •X1, x2, …, xk.
- •Свойства среднего
- •Основные определения
- •Относительная флуктуация
- •Характеристики случайНой непрерывНой величиНы
- •Биномиальное распределение
- •Распределение Пуассона
- •Нормальное распределение Гаусса
- •Пример 1. Распределение времен свободного пробега электрона металла
- •Пример 2.Дрейф электронов металла в электрическом полеЕ
- •Пример 3. Ток вакуумного диода
- •Пример 4. Броуновское движение
Характеристики случайНой непрерывНой величиНы
Случайной непрерывной величиной является, например, проекция скорости молекулы газа, хаотически меняющаяся благодаря столкновениям.
Плотность вероятности. Пусть случайная величина x принимает непрерывные значения в некотором интервале. Вероятность обнаружения x в единичном интервале около выбранного значения называется плотностью вероятности результата
![]() .
(1.11)
.
(1.11)
Аналогично
определение скорости
![]() ,
которая является перемещением за единицу
времени.
,
которая является перемещением за единицу
времени.
Вероятность
получения результата в интервале
![]() равна
равна
![]() .
.
Пример:
Пусть
![]() – скорость частицы идеального газа.
Частицы движутся хаотически и при
столкновениях меняют свои скорости.
Вероятность обнаружения частицы со
скоростью в интервале
– скорость частицы идеального газа.
Частицы движутся хаотически и при
столкновениях меняют свои скорости.
Вероятность обнаружения частицы со
скоростью в интервале![]() равна
равна
![]() ,
,
где
![]() –концентрация
частиц со скоростями в интервале
–концентрация
частиц со скоростями в интервале
![]() шириной
шириной![]() ;
;
n – концентрация частиц со всеми скоростями;
плотность вероятности
![]()
– вероятность обнаружения частицы со скоростью в единичном интервале около значения v.
Условие нормировки для непрерывного распределения
![]() .
(1.12)
.
(1.12)
Средние значения
![]() ,
,
![]() .
(1.13)
.
(1.13)
Характеристическая
функция
![]() является фурье-образом плотности
вероятности
является фурье-образом плотности
вероятности
 .
(1.14)
.
(1.14)
Обратное преобразование Фурье выражает функцию распределения через характеристическую функцию
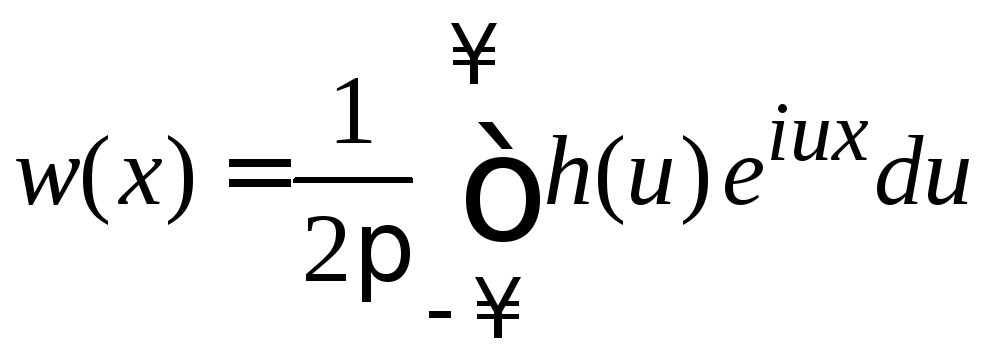 .
(1.15)
.
(1.15)
Из (1.14) находим нормировку вероятности
![]() .
(1.16)
.
(1.16)
Для среднего значения из (1.13) и (1.14) получаем
 .
(1.17)
.
(1.17)
Рассмотрим дискретные распределения.
Биномиальное распределение
Имеются N независимых частиц или N независимых попыток с положительным или отрицательным результатами. Если известна вероятность p положительного результата для одной частицы или попытки, то вероятность положительного результата для любых n частиц или попыток описывается биномиальным распределением
 ,
(1.26)
,
(1.26)
где
![]() ;
;
![]() ;
;
 –биномиальный
коэффициент;
–биномиальный
коэффициент;
![]() ;
;
![]() ,
,![]() ,
,
 ,
,
 ,
,
 ,
,![]() .
.
Распределение обосновал Бернулли, результат опубликован в 1713 г.

Якоб Бернулли (1654–1705)
Для
доказательства (1.26) рассмотрим идеальный
газ из N
тождественных частиц в объеме V,
все точки которого равноправны. Получим
вероятность обнаружения n
любых частиц в объеме
![]() .
.
Вероятность найти определенную частицу в объеме V согласно (1.5)
![]() .
.
Вероятность найти определенную частицу вне объема V
![]() .
.
Эти несовместимые события образуют полный набор и удовлетворяют условию нормировки.
Вероятность найти n определенных частиц в объеме V согласно теореме об умножении вероятностей независимых событий (1.6) равна
 .
Вероятность найти (N
– n)
определенных частиц вне объема V
равна
.
Вероятность найти (N
– n)
определенных частиц вне объема V
равна
 .
.Вероятность найти одновременно n определенных частиц в объеме V и (N – n) других частиц вне этого объема
![]() .
.
Взаимная перестановка тождественных частиц дает состояние, не отличимое от исходного. Число таких состояний есть число сочетаний n частиц из общего числа N и равно биномиальному коэффициенту
 .
.Тогда вероятности найти n любых частиц в объеме V и (N – n) любых других частиц вне V равна (1.26).
Условие нормировки. Складываем вероятности всех возможных случайных результатов
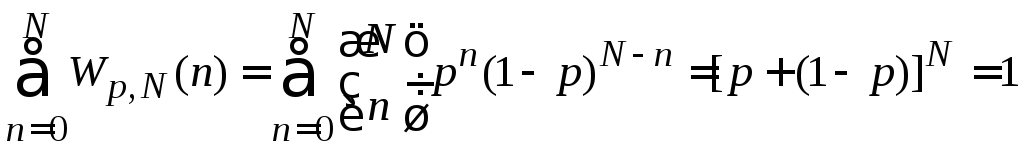 ,
,
где использована формула бинома Ньютона
 .
.
Отсюда идет название распределения.

Исаак Ньютон (1642–1727)
Производящая функция биномиального распределения
![]() .
(1.27)
.
(1.27)
Для доказательства (1.27) подставляем биномиальное распределение (1.26)

в определение производящей функции (П.1.14)
 .
(1.27а)
.
(1.27а)
Используем бином Ньютона
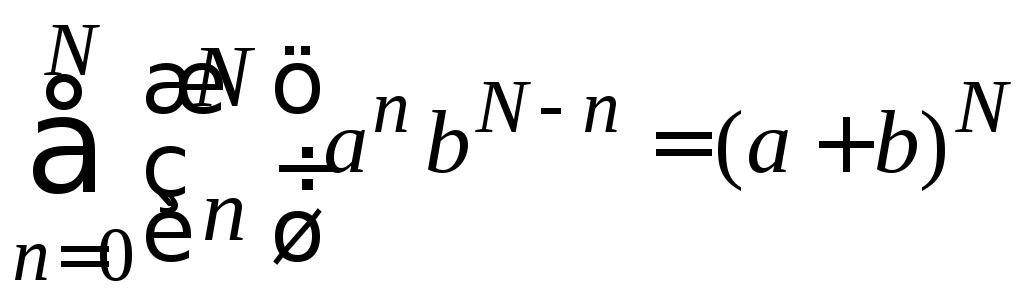 ,
,
и получаем (1.27).
Выполняется условие нормировка (П.1.16) для биномиального распределения согласно
![]() .
.
Среднее число частиц в объеме V получаем подстановкой производящей функции (1.27)
![]()
в (П.1.17)
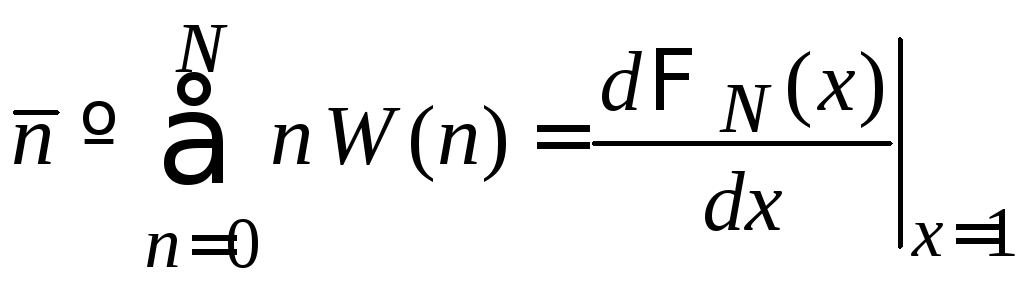 .
.
Находим
![]() ,
(1.28)
,
(1.28)
где
учтено
![]() .
Результат очевиден, поскольку
.
Результат очевиден, поскольку![]() – средняя концентрация.
– средняя концентрация.
Из (1.28) выражаем вероятность некоторого признака у частицы
![]()
и подставляем в биномиальное распределение (1.26)
 .
.
Получаем
вероятность
наличия некоторого признака у n
частиц,
если этот
признак наблюдается в среднем у
![]() частиц из общего числаN
частиц из общего числаN
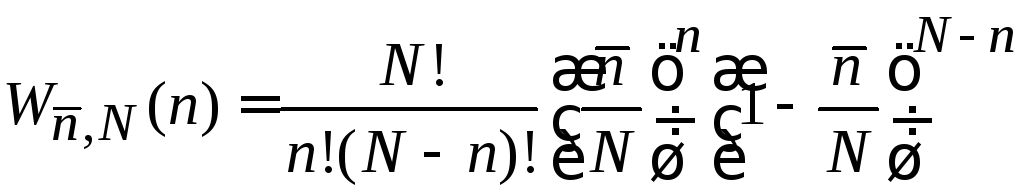 .
(1.29)
.
(1.29)
В
частности, отсутствия признака у всех
частиц соответствует
![]() ,
вероятность этого
,
вероятность этого
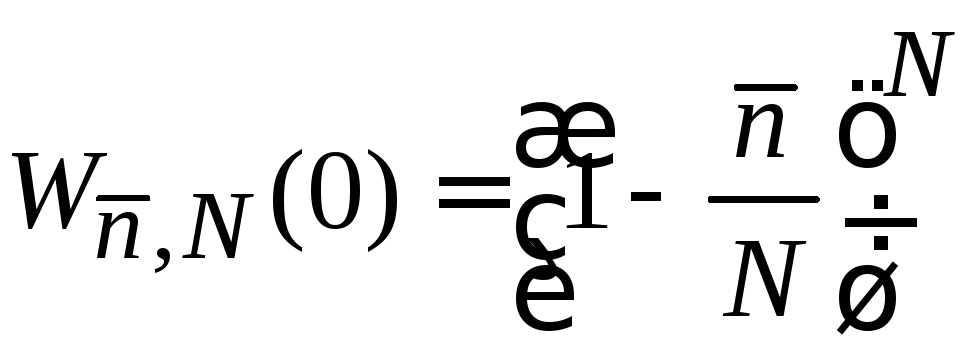 .
.
Наличия
признака у всех частиц соответствует
![]() ,
и наблюдается с вероятностью
,
и наблюдается с вероятностью
 .
.
Среднеквадратичное число частиц и дисперсия. Подставляем производящую функцию (1.27)
![]()
в (П.1.18)
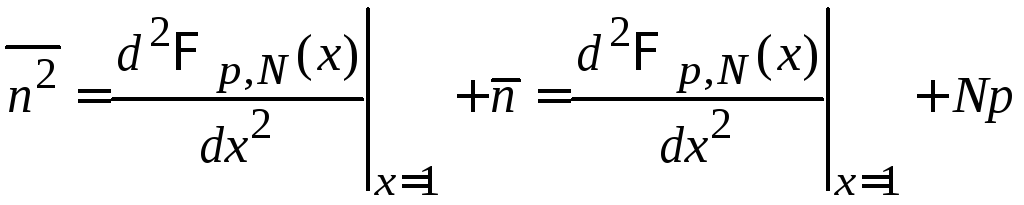 .
.
Находим среднее квадратичное
![]() (1.30)
(1.30)
и дисперсию
![]() .
(1.31)
.
(1.31)
Дисперсия
равна нулю при
![]() и
и![]() ,
при
,
при![]() достигается максимальное значение
достигается максимальное значение![]() .
.
График
распределения
для
![]() ,
,
![]() ,
,
![]() показан на рис. 1.1, a.
показан на рис. 1.1, a.

а б
Рис. 1.1. Распределения биномиальное (а)
и
Пуассона (б) дляN= 10,
![]() ,р= 0,45
,р= 0,45
