Статистические характеристики фононного газа

Вероятность обнаружения фонона с частотой в интервале в единице объема кристалла равна

,

где

;

n – концентрация фононов; V – объем кристалла. Используем

, ,

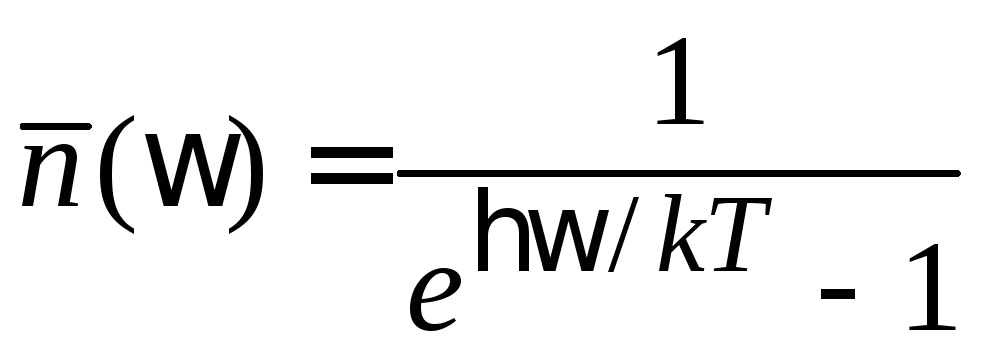находим

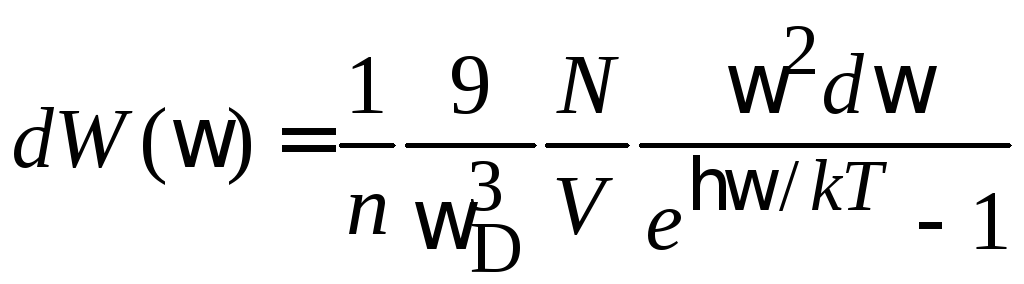, (П.12.1)

где N – числом узлов в кристалле. Из условия нормировки

находим концентрацию фононов

.

Заменяем , используем, и получаем

. (П.12.2)

Низкая температура . Верхний предел интеграла считаем бесконечным

находим

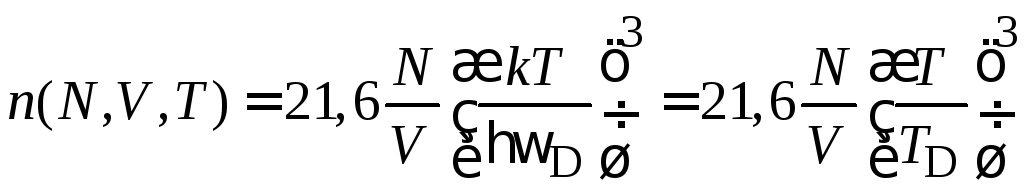. (П.12.3)

При низкой температуре в трехмерном кристалле средняя концентрация фононов пропорциональна числу узлов в единице объема кристалла и третьей степени температуры. При получаем– концентрация фононов гораздо меньше концентрации узлов при низкой температуре.

Вероятность обнаружения фонона в единице объема в единичном интервале частоты около значения  выражаем из (П.12.1) и (П.12.3)

, ,

находим

. (П.12.4)

График функции совпадает с графиком распределения Максвелла по модулю скорости.

Максимум функции

,

где , соответствует наиболее вероятной частотефонона. Из условия

получаем уравнение

.

Численное решение дает

.

Наиболее вероятная энергия фонона

.

Учитывая (4.72)

,

находим наиболее вероятную длину волны

,

где d – постоянная решетки. При низкой температуре наиболее вероятная длина волны фонона во столько раз превышает постоянную решетки, во сколько раз температура кристалла меньше температуры Дебая.

Теплоемкости электронного газа и кристаллической решетки z-валентного металла

Теплоемкость вырожденного газа NZ электронов при согласно (П.10.19) равна

.

Теплоемкость кристаллической решетки из N узлов при по закону Дебая (4.75)

.

Зависимости от температуры показаны на рисунке.

При теплоемкости выравниваются

,

,

откуда

. (П.12.8)

Учитывая , находим

.

При нормальной температуре электронный газ не дает существенного вклада в теплоемкость металла. Теорема классической физики о распределении энергии по степеням свободы не применима для квантовой области.

Конденсация Бозе–Эйнштейна

В газе из атомов бозонов при достаточно низкой, но конечной температуре, часть атомов полностью теряет свою кинетическую энергию и импульс. Такие атомы называются бозе-конденсатом от лат. condenso – «сгущаю». Волновые функции атомов конденсата согласованы по фазе. На этой основе созданы атомные лазеры, испускающие атомы с когерентными волновыми функциями.

Явление полной потери кинетической энергии у части идеального бозонного газа при понижении температуры теоретически открыл Эйнштейн в 1925 г. Процесс называется бозе-конденсация частиц в импульсном пространстве. Причина конденсации связана с поведением химического потенциала бозонов. Будучи отрицательным, он увеличивается при уменьшении температуры и достигает наибольшего допустимого значения при. Химический потенциал газа зависит не только от температуры, но и от концентрации частиц. Дальнейшее понижение температуры сохраняетза счет уменьшения числа частиц в газовой фазе, избыточные атомы выпадают в конденсат, полностью теряя свою энергию и импульс. Явление исследовали братья Лондоны в 1938 г.

Хайнц Лондон (1907–1970) Фриц Лондон (1900–1954)

Получить конденсацию экспериментально не удавалось 50 лет, поскольку при низкой температуре межатомное взаимодействие притягивает атомы друг к другу, образуются кластеры и возникает жидкое или твердое состояние до начала бозе-конденсации. Кластер образуется при столкновении трех и более частиц, что вероятнее при высокой концентрации. При низкой концентрации преобладают парные столкновения, обеспечивающие установление теплового равновесия. Для предотвращения образования кластеров нужно снижать концентрацию газа. Метастабильный бозе-конденсат в разреженных газах атомов рубидия, натрия, лития получили Кеттерле, Виман и Корнелл в 1995 г. Атомы водорода конденсированы в 1997 г. Конденсат обладает уникальными свойствами – при температуре дисперсия света столь велика, что скорость света в бозе-конденсате атомовNa составляет , скорость звука. Для сравнения скорость света в вакууме, в алмазе.

Вольфганг Кеттерле, Карл Виман, Эрик Корнелл

Атомы бозоны. Спин атома складывается из спинов электронов оболочки и нуклонов ядра, у всех этих частиц спиновое число 1/2. У нейтрального атома число электронов равно числу протонов, их общий спин целочисленный. В результате спин атома определяется числом нейтронов. Бозонами являются атомы с четным числом нейтронов, например: