Фотонный газ

Фотон – квант электромагнитного излучения, движется в вакууме со скоростью света и характеризуется волновым вектором, энергией и поляризацией, в этот набор не входит пространственное положение фотона и фаза волны. В отличие от электрона для фотона невозможно ввести эрмитовый оператор координаты, положение фотона становится определенным только в момент его излучении атомом и в момент регистрации детектором. Отсутствует эрмитовый оператор фазы и фотон нельзя представлять гармонической волной. Существует оператор числа фотонов, множество фотонов образует электромагнитную волну. Двойственность волна-частица проявляется в том, что неопределенность числа фотонов и неопределенность фазы волнысвязаны соотношением

.

Чем точнее измеряется фаза волны, тем менее известно число фотонов в волне, и наоборот. В состоянии плоской, монохроматической, гармонической волны фотон имеет определенную энергию и импульс, при этом координата фотона и число фотонов в волне не определены.

Рассмотрим фотонный газ в замкнутой макроскопической полости, созданный тепловым излучением стенок. Фотоны является бозонами, их взаимное интерференционное «притяжение» приводит к согласованному перемещению, состоянием фотонного газа является электромагнитная волна.

Фотон как квант энергии теплового излучения тела ввел Планк в 1900 г. и как квант электромагнитной волны при фотоэффекте ввел Эйнштейн в 1905 г. Название от др.-греч.  – «свет» дал Льюис в 1926 г. Импульс p и энергия ε фотона определяются длиной λ и частотой ω, ν волны

,

, (4.53)

, ,

где С – скорость света. Спин фотона . Масса фотона равна нулю, он движется со скоростью света. Для такого движения теория относительности допускает только две проекции спина – по- и против скорости, что соответствует двум типам поляризации света

.

Фотонный газ в полости. Электромагнитное излучение испускается и поглощается заряженными частицами стенок полости, переходящими с одного энергетического уровня на другой при участии теплового движения и изменяющими свою энергию квантами, носителями которых являются фотоны. Множество фотонов в полости образует фотонный газ. После испускания и до поглощения фотон не локализован в пространстве, состоянием фотонного газа является электромагнитная волна. Плотность состояний получается на основе дисперсионного соотношения путем использования фазового пространства. Температуру стенок полости считаем одинаковой и постоянной, тогда фотонный газ в полости равновесный. Среднее число фотонов, связанных с волной, определяется температурой и выражается распределением Бозе–Эйнштейна.

Плотность состояний. Ранее показано, что в единице объема в интервале частот находитсячисло состояний, т. е. независимых волн (П.8.9а)

.(4.54)

Например, для излучения красного цвета мкм получаем в единице объема число состояний с/м³ с частотами в единичном интервале около значения рад/с.

Химический потенциал. У фотона нет сохраняющегося заряда. Число фотонов меняется при излучении и поглощении света заряженными частицами, поэтому химический потенциал фотона не может быть получен из условия нормировки на число частиц.

При термодинамическом равновесии излучения в полости с фиксированными T и V свободная энергия минимальна

.

Левая сторона равенства является определением химического потенциала

,

следовательно, для теплового равновесного излучения

 = 0. (4.55)

Концентрация фотонов. Из распределения Бозе–Эйнштейна (4.10)

получаем среднее число тепловых фотонов в волне с частотой 

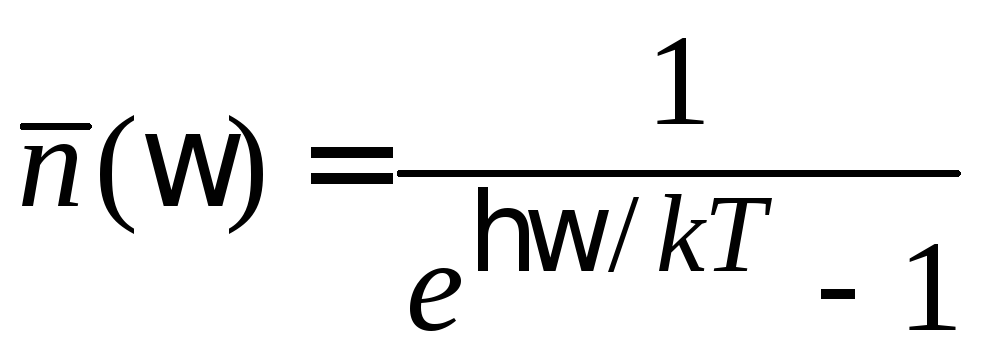. (4.56)

На поверхности Солнца К,эВ, для оптических фотонов с энергиейэВ заселенность состояний мала. Заселенность выходит на единицу при температуре

К.

Для сравнения, у лазера заселенность моды излучения и из (4.56) находим,, тогда,. Поэтому лазерное излучение имеет высокую эффективную температуруи способно резать металл.

Учитывая число волн в единице объема (4.54)

,

находим концентрацию фотонов с частотой в интервале

. (4.57)