Парамагнетизм газа

Парамагнетизм вещества означает, что магнитное поле вещества превышает внешнее поле. Магнетизм электронного газа вызван спиновым магнитным моментом электрона. Проекция спина электрона на направление поля равна , проекция спинового магнитного момента. Во внешнем магнитном поле электрон со спином против поля и с магнитным моментом по полю имеет меньшую энергию и большую вероятность реализации, чем обратное направление. В результате по направлению поля ориентировано большее число магнитных моментов, чем в обратную сторону. Это означает парамагнетизм электронного газа.

Рассмотрим идеальный газ N частиц со спином и магнитным моментомв объемеV при температуре T в магнитном поле В. Проекции спина S и спинового магнитного момента

на направление поля квантуются. Энергия магнитного момента в магнитном поле

получает значения

, .

Получим распределение частиц по уровням энергии.

Статистическую сумму для магнитных состояний частицы находим из (3.15)

.

Вырождение отсутствует , тогда

, (П.9.11)

где относительная магнитная энергия

.

Вероятности состояний (3.14а)

равны

, .

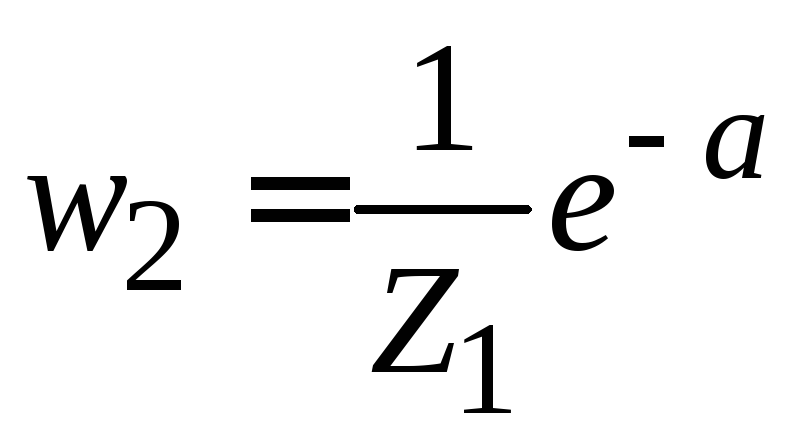Средняя энергия частицы

. (П.9.12)

Намагниченность системы. Средняя проекция магнитного момента частицы

. (П.9.13)

В сильном поле ,,,

все магнитные моменты направлены по полю, возникает насыщение намагниченности.

В слабом поле ,,

.

Магнитный момент системы N частиц

.

Система частиц со спином 1/2 проявляет парамагнитные свойства – установил Паули в 1926 г. Полученные результаты

,

являются следствием – вероятность основного состояния больше вероятности возбужденного состояния.

В классическом пределе при из (П.9.13)

получаем , что соответствуеттеореме Бора–Ван-Лёвен – классическая система не проявляет магнитных свойств.

Магнитный момент единицы объема, т. е. намагниченность системы во внешнем поле согласно (П.9.13) равна

, (П.9.13а)

где – концентрация частиц.

Магнитная восприимчивость

.

С учетом ,получаем

. (П.9.13б)

Магнитная восприимчивость увеличивается при понижении температуры и при увеличении концентрации частиц.

Магнетизм электронного газа металла. Формула (П.9.13б) не применима к электронному газу металла, где согласно принципу Паули на каждом уровне энергии может находиться не более двух электронов с противоположными проекциями спина.

При все уровни энергии заполнены до уровня Ферми, где μ – химический потенциал. Уровни выше свободны, и внешнее магнитное поле не меняет магнитного состояния.

При уровни заполнены частично в полосе ширинойоколо уровня химического потенциала μ. Только эти электроны числомв единице объема, гдеn – концентрация, реагируют на внешнее магнитное поле. С учетом получаем намагниченностьи восприимчивость, не зависящую от температуры и гораздо меньшую (П.9.13б).

Магнитное охлаждение. Если поле изменяется адиабатически, то есть настолько быстро, что теплообмена с окружающей средой не происходит, то сохраняются заселенность уровней и средняя проекция магнитного момента (П.9.13)

.

Следовательно, изменяется температура магнетика

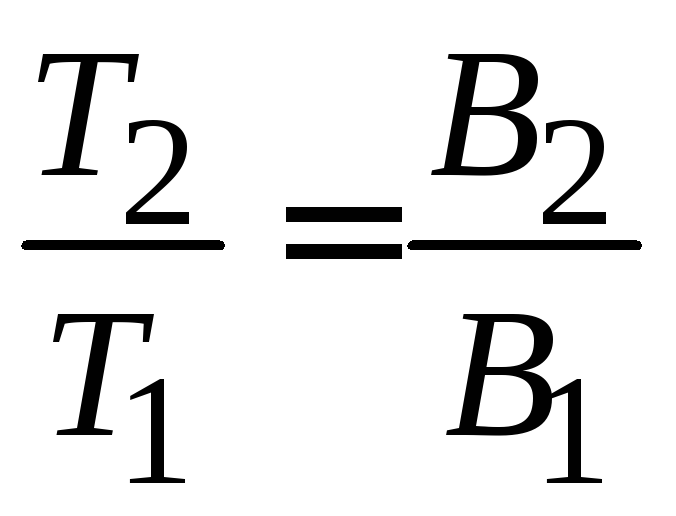. (П.9.13в)

Адиабатическое уменьшение магнитного поля охлаждает систему. Причина в том, что снижение магнитного поля увеличивает среднюю магнитную энергию частицы согласно (П.9.12) . Поскольку теплообмена с окружением не происходит, то это оттягивает тепловую энергию системы к магнитным моментам и тепловое движение ослабевает.

Метод магнитного охлаждения на основе парамагнитных солей (сульфат гадолиния, хромокалиевые квасцы) предложили Петер Дебай и Уильям Джиок в 1926 г. Метод применяется для получения температур от 0,3 К до 510^–3 К. При меньшей температуре становится существенным взаимодействие между магнитными моментами, выстраивающее их параллельно друг другу, и они становятся зависимыми.

Самопроизвольная намагниченность. У намагниченной системы магнитные моменты выстроены параллельно и создают магнитное поле

,

где M – магнитный момент единицы объема; – средняя проекция магнитного момента частицы;n – концентрация частиц. Система может увеличивать поле самопроизвольно. Борис Львович Розинг в 1892 г. и Пьер Вейсс в 1907 г. предложили в выражении для магнитного момента единицы объема (П.9.13а)

добавить собственное поле к внешнему намагничивающему полю

,

тогда намагниченность системы

.

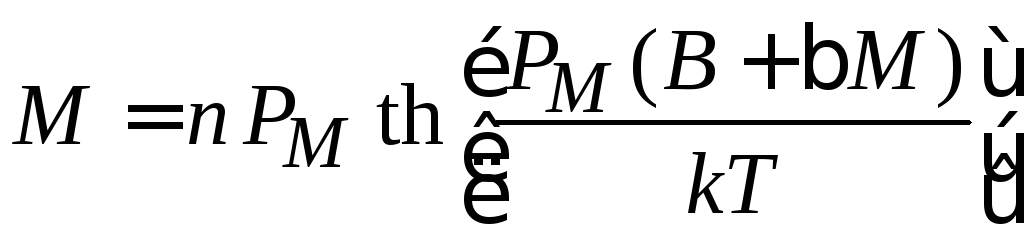При отсутствии внешнего поля получаем дляM нелинейное уравнение

.

Замена дает

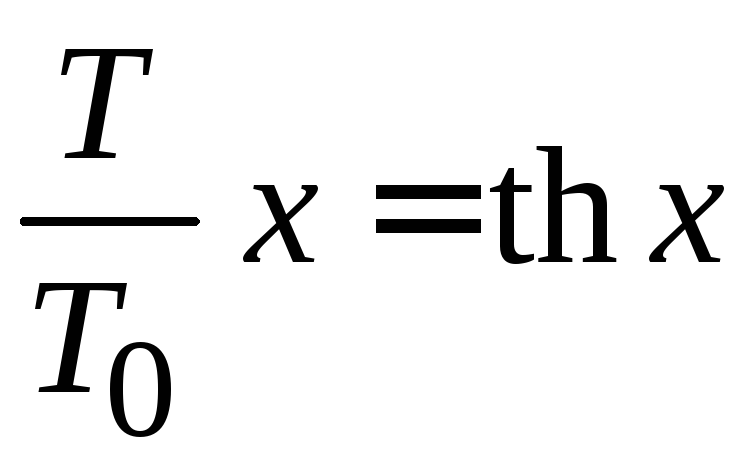, (П.9.14)

где

(П.9.15)

– критическая температура Кюри.

При функциярастет медленнееx, поэтому при температуре выше критической равенство (П.9.14) не выполняется. Остается лишь решение. Следовательно,при достаточно высокой температуре спонтанная намагниченность отсутствует.

При температуре ниже критической уравнение (П.9.14) имеет не равные нулю решения и система самопроизвольно намагничивается. Происходит фазовый переход второго рода – изменяется внутренняя симметрия системы, появляется ферромагнитное состояние в виде спонтанно намагниченных областей –доменов или полей Вейсса. При малых x используем и (П.9.14) получает вид

,

откуда

.

С учетом 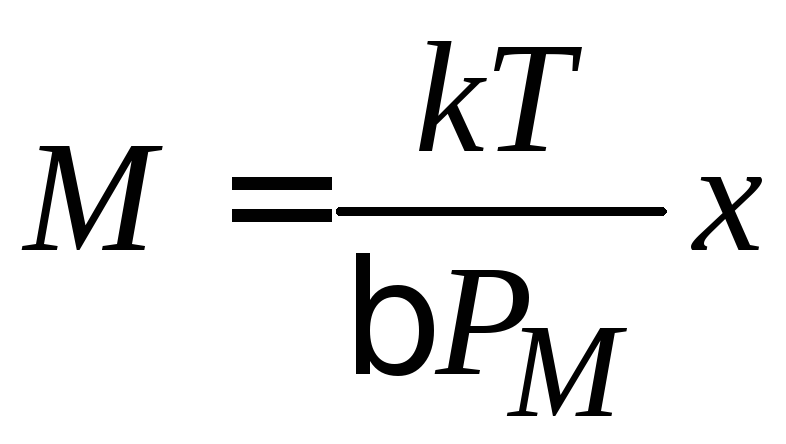находим спонтанную намагниченность

. (П.9.16)

Максимум достигается при

.

Сравнение (П.9.15) и (П.9.16) с экспериментом, дает . Магнитное поле не может создать столь сильного взаимодействия магнитных моментов. Яков Ильич Френкель и независимо Вернер Гейзенберг показали в 1928 г., что электростатическое взаимодействие между электронами атомов сопровождается квантовым обменным взаимодействием, существенно превышающим магнитное взаимодействие, и этим объясняется спонтанная намагниченность ферромагнетика.