Газ гармонических осцилляторов

Идеальный газ состоит из двухатомных молекул массой μ, являющихся линейными гармоническими осцилляторами, колеблющимися с частотой . Найдем статистическую сумму, среднюю энергию частицы при температуреT, теплоемкость колебательного движения газа и среднее квадратичное смещение атома в молекуле.

Для линейного гармонического осциллятора используем результаты квантовой механики

, ,

Подстановка в статистическую сумму частицы (3.15)

дает

,

где относительная температура

,

эффективная температура колебаний

.

Чем меньше масса атома, тем выше частота колебаний и больше эффективная температура, например:

, ,.

По формуле геометрической прогрессии

, ,,

получаем

, (П.9.1)

Вероятность энергии находим из (3.14)

.

_{Используем}

,

,

_{и из (П.9.1), получаем}

. (П.9.1а)

Вероятность энергии экспоненциально убывает с увеличением номера состояния n.

Средняя энергия осциллятора следует из (3.17б)

.

Используем

, ,

,

С учетом

,

,

,

получаем

. (П.9.2)

Среднее число квантов у осциллятора при температуре T. Осциллятор в состоянии n содержит n квантов энергии величиной . Эти кванты создаются тепловой энергией. Получим среднее число квантовпри температуреT. Усредняем энергию состояния

,

находим

,

Подставляем (П.9.2)

,

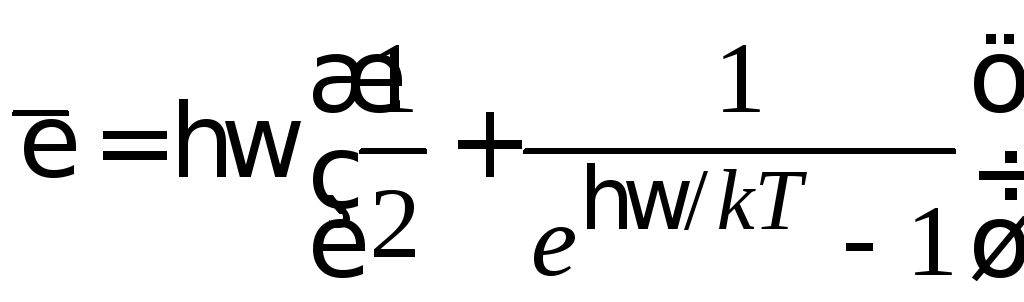получаем средний номер активизированного состояния, или среднее число квантов энергии у осциллятора с частотой ω при температуре Т

. (П.9.2а)

График показан на рисунке.

При низкой температуре , где, находим

.

При

,

следовательно, при высокой температуре среднее число квантов равно отношению тепловой энергии к энергии кванта.

Колебательная теплоемкость молекулы

.

Используем (П.9.2)

,

получаем

. (П.9.2б)

При высокой температуре , где, в (П.9.2)

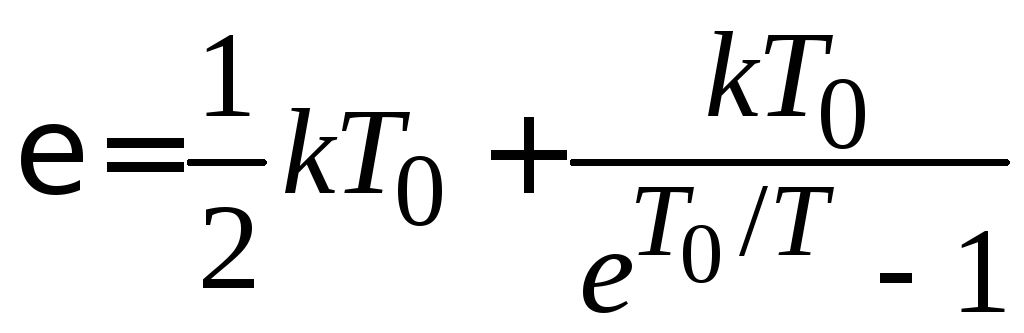
экспоненту разлагаем в ряд и оставляем первые три слагаемые

,

тогда

.

При высокой температуре колебательная теплоемкость молекулы

не зависит от температуры, и квантовая статистика переходит в классическую.

При низкой температуре ,в (П.9.2б)

пренебрегаем единицей в знаменателе и получаем

.

При находим, и выполняется третье начало термодинамики – теплоемкость обращается в нуль при . Это противоречит теореме классической физики о равном распределении энергии по степеням свободы.

Тепловое расширение определяется зависимостью среднего квадратичного смещения атома в молекуле от температуры Т. Согласно квантовой механике квадрат смещения на уровне n

,

где . Используем вероятность состояния (П.9.1а)

,

получаем среднее квадратичное смещение

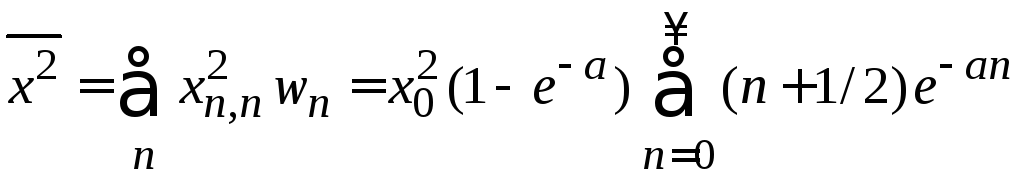. (П.9.6)

Вычисляем суммы

,

,

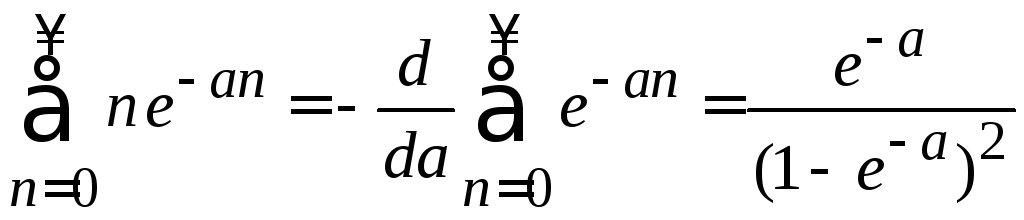находим

. (П.9.7)

График показан на рисунке.

При высокой температуре из (П.9.7) получаем

,

следовательно, размер молекулы линейно увеличивается с ростом температуры.

При низкой температуре размер фиксированнный

.

Вращательное движение

Идеальный газ состоит из двухатомных молекул, каждая из которых является пространственным ротатором с моментом инерции J. Найдем статистическую сумму вращательного движения, внутреннюю энергию и теплоемкость при температуре T.

Согласно квантовой механике, гамильтониан пространственного ротатора

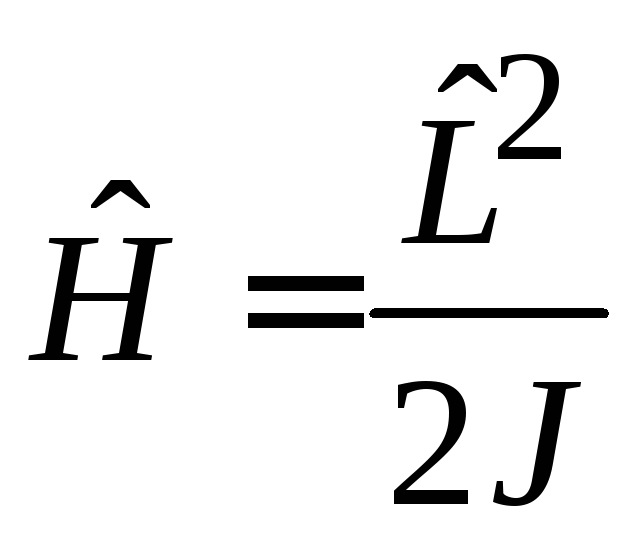
имеет собственные значения

,

где –орбитальное квантовое число;

– эффективная температура вращения, в частности

, ,.

Вне магнитного поля энергия не зависит от проекции орбитального момента, поэтому для определенного l кратность вырождения равна числу проекций орбитального момента

.

Используя (3.29)

,

находим статистическую сумму вращательного движения молекулы

, (П.9.8)

где для молекулы из разных атомов;для одинаковых атомов, поскольку их перестановка не меняет физического состояния, и такое состояние учитывается однократно.

Среднюю энергию молекулы получаем из (3.27) и (П.9.8)

. (П.9.9)

При высокой температуре расстояния между энергетическими уровнями малы по сравнению с тепловой энергией, поэтому суммирование заменяем интегрированием. Из (П.9.8) находим

,

тогда

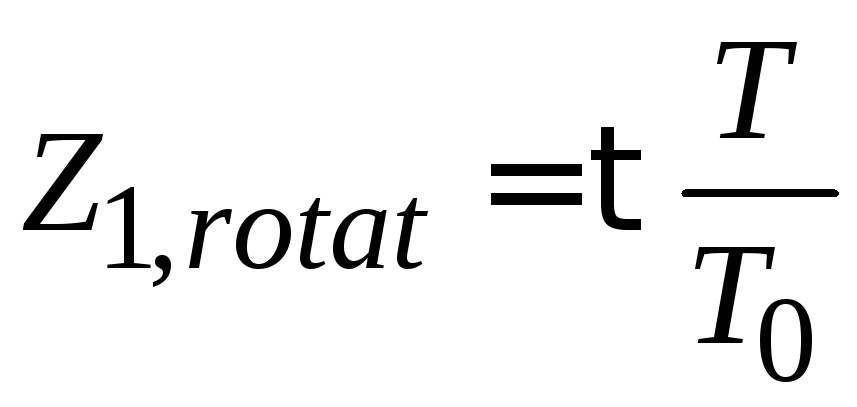. (П.9.10)

Средняя энергия

согласуется с (П.3.12) классической теории.

При низкой температуре в суммах (П.9.8) и (П.9.9) наиболее существенны первые слагаемые, тогда

,

,

. (П.9.11)

При теплоемкость стремится к нулю согласно третьему началу термодинамики.