Каноническое распределение квантового идеального газа

Идеальный газ с фиксированным числом частиц N, объемом V и температурой T описывается каноническим распределением. Распределение позволяет найти:

1. Вероятность определенной энергии системы;

2. Вероятность определенной энергии частицы;

3. Термодинамические характеристики системы.

При получении функции квантового распределения учитываем:

1. Дискретность спектра энергии системы частиц, где;

2. Дискретность спектра энергии каждой частицы, где;

3. Кратность вырождения состояний системы по энергии 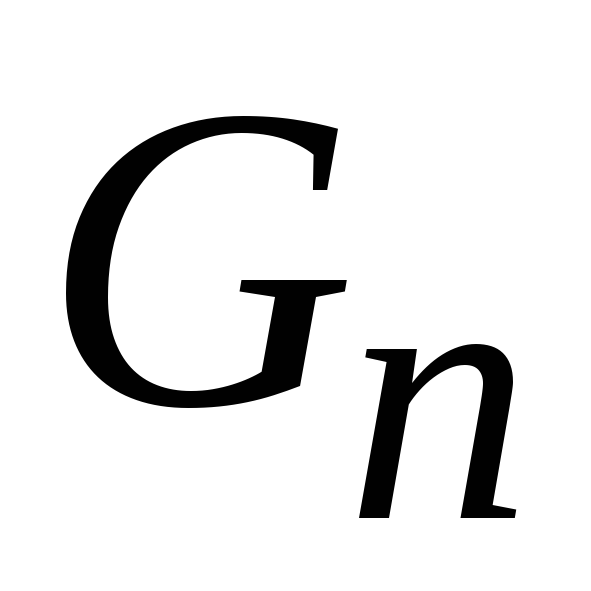– число разных состояний с одинаковой энергией, и кратность вырождения состояний частицы;

4. Принцип запрета Паули для фермионов;

5. Правило соответствия – соотношения между динамическими характеристиками одинаковы в классической и квантовой теориях.

Каноническое распределение системы по состояниям. Из канонического распределения классической системы (2.77)

по правилу соответствия получаем вероятность нахождения квантовой системы в невырожденном состояния n с энергией

. (3.19)

Каждое из вырожденных состояний с энергией имеет одинаковую вероятность реализации. По теореме о несовместимых событиях вероятность реализации любого из них в раз больше. В результате система имеет энергию с вероятностью

. (3.20)

Вероятность экспоненциально убывает с увеличением энергии, что согласуется с распределением Максвелла–Больцмана. Нормировка вероятности (3.20)

дает статистическую сумму системы

. (3.21)

Термодинамические величины являются средними по статистическому ансамблю. Система не изолирована, и ее полная энергия флуктуирует на микроскопическом уровне. Внутренняя энергия равна среднему значению полной энергии системы

,

где использована вероятность (3.20). Сравниваем с (3.21)

,

находим

. (3.22)

Результат не отличается от классической формулы (2.93), подтверждая правило соответствия.

Энтропию получаем аналогично (2.100):

. (3.23)

Состояние системы складывается из состояний составляющих независимых частиц. Получим распределение по энергии для частицы газа.

Каноническое распределение частицы по состояниям. Применяем (3.20)

к частице газа, рассматривая остальные частицы как термостат. Получаем вероятность того, что частица находится на уровне энергии с кратностью вырождения

. (3.25)

Нормировка вероятности

дает статистическую сумму частицы

. (3.26)

Аналогично (3.22)

получаем среднюю энергию частицы

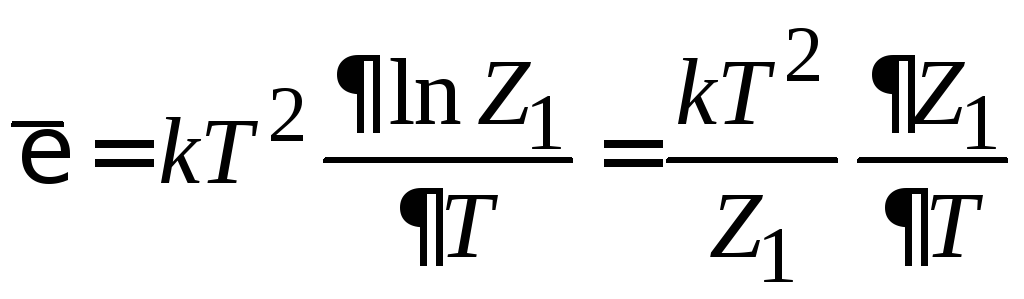. (3.27)

Тепловое движение частицы складывается из независимых видов движений: поступательного, вращательного, колебательного, изменения внутреннего состояния. Полная энергия равна сумме энергий независимых движений

.

Для вида движения α вводим вероятность того, что частица имеет энергию с кратностью вырождения. Аналогично (3.25)

находим

. (3.28)

Нормировка дает

. (3.29)

По теореме умножения вероятностей независимых событий получаем вероятность того, что частица имеет энергию

. (3.30)

Поступательное (translation) движение в макроскопическом объеме имеет квазинепрерывный спектр энергии. По правилу соответствия квантовая статистическая сумма частицы при больших квантовых числах не отличается от классического выражения (2.83)

. (3.31)

Колебательное (oscillation) движение. Далее показано, что для двухатомной молекулы с частотой собственных колебаний статистическая сумма

, (3.32)

где эффективная температура .

Вращательное (rotation) движение. Для молекулы с моментом инерции J далее получено

, (3.33)

где суммирование ведется по всем возможным значениям орбитального числа l; эффективная температура ;для молекулы из двух разных атомов,для молекулы из двух одинаковых атомов.

Независимые виды движений. По теореме умножения вероятностей независимых событий выполняется

. (3.34)

Для N тождественных частиц используем (2.80)

, (3.35)

где учтено, что состояния, отличающиеся перестановкой частиц, числом N! физически не различимы и должны учитываться однократно. Из (3.34) и (3.35) находим

. (3.36)

Получим статистические суммы и средние энергии для конкретных систем и докажем (3.32) и (3.33).