Эффект Зеемана

Сдвиг уровня энергии электрона атома в магнитном поле вызван взаимодействием магнитного момента электрона с магнитным полем и называется эффектом Зеемана. Магнитный момент пропорционален орбитальному моменту, поэтому величина сдвига пропорциональна магнитному числу.

Полуклассическое рассмотрение. В водородоподобном атоме энергия электрона вырождена по квантовым числам l и m, т. е. от них не зависит. Орбитальное движение электрона в атоме создает магнитный момент (1.37) с проекцией

.

При помещении атома в магнитное поле магнитный момент взаимодействует с полем и получает энергию

, (7.41)

пропорциональную магнитному числу m. В результате уровень водородоподобного атома с орбитальным числом l расщепляется в магнитном поле на подуровней.Магнитное поле снимает вырождение по магнитному числу. Явление обнаружил Зееман в 1896 г.

Питер Зееман

(1865–1943)

Квантовомеханическое рассмотрение. Электрон в магнитном поле описывается гамильтонианом (7.18)

,

где ;– гамильтониан электростатического взаимодействия электрона в атоме. В слабом магнитном поле отбрасываем малое слагаемое кинетической энергии, пропорциональное, тогда

Для постоянного однородного магнитного поля , направленного по осиz, используем осесимметричную калибровку векторного потенциала

,

, ,.

Проекции оператора полного импульса

коммутируют с соответствующими проекциями векторного потенциала

.

В результате выполняются

,

тогда

.

где учтено

–оператор орбитального момента;

.

Гамильтониан

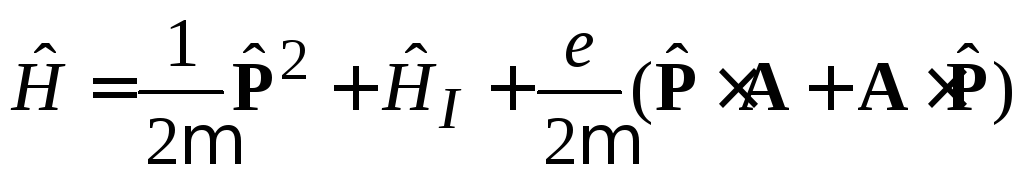
получает вид

,

где

–гамильтониан электрона в атоме без учета магнитного поля;

–магнетон Бора.

Гамильтониан подставляем в стационарное уравнение Шредингера

.

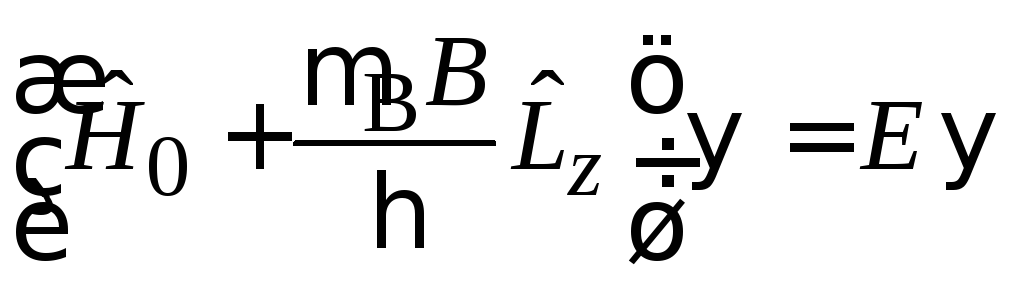Операторы

, ,

взаимно коммутируют, их собственные значения

E, l, m

являются параметрами состояния

.

Состояние с определенной проекцией орбитального момента удовлетворяет

.

Для атома вне магнитного поля

.

Из уравнения

получаем энергию

,

совпадающую с (7.41). Здесь Е₀ – энергия электрона без учета магнитного поля; m – магнитное квантовое число.

Результат для энергии совпадает с результатом полуклассической квантовой механики.

47