Уровни Ландау

Состояния заряда в магнитном поле на основе уравнения Шредингера исследовал Ландау в 1930 г. Он получил Нобелевскую премию 1962 г. за работы по сверхтекучести и сверхпроводимости жидкого гелия.

Лев Давидович Ландау

(1908–1968)

Получим состояния заряда q массой μ в однородном стационарном магнитном поле В.

Заряд в полуклассической теории. При движении заряда в плоскости, перпендикулярной магнитному полю, траектория является окружностью, радиус траектории и импульс частицы квантуются

,

,

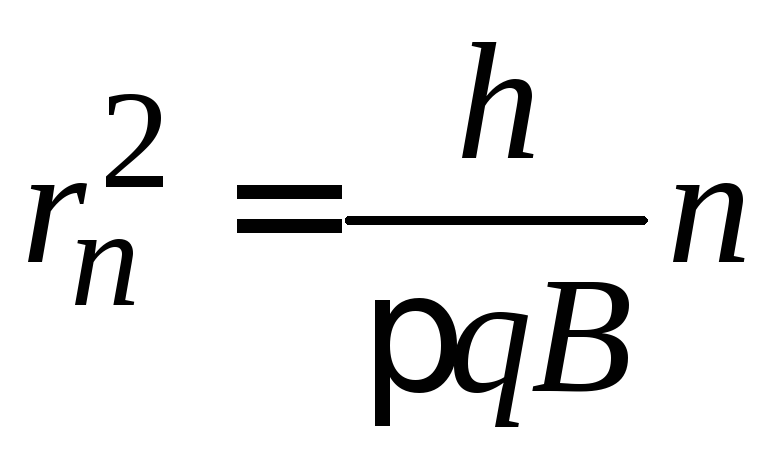Вращение происходит с циклотронной частотой (1.24)

,

спектр энергии дискретный

,

совпадает со спектром гармонического осциллятора.

Рассмотрим эту задачу в рамках квантовой механики, где отсутствует понятие траектории, используя стационарное уравнение Шредингера.

Гамильтониан заряда q в магнитном поле (7.17)

, ,

запишем в декартовых координатах. Ось z направляем по полю

.

Векторный потенциал связан с индукцией

.

В декартовых координатах соотношениям

, ,

удовлетворяет потенциал в калибровке Ландау

.

Получаем гамильтониан заряда

. (5.46)

Параметрами состояния заряда являются собственные значения операторов, коммутирующих с гамильтонианом. Их собственные функции входят сомножителями в функцию состояния заряда. Для операторов проекций полного импульса выполняется

, .

Следовательно, состояние частицы характеризуется значениями

, ,,

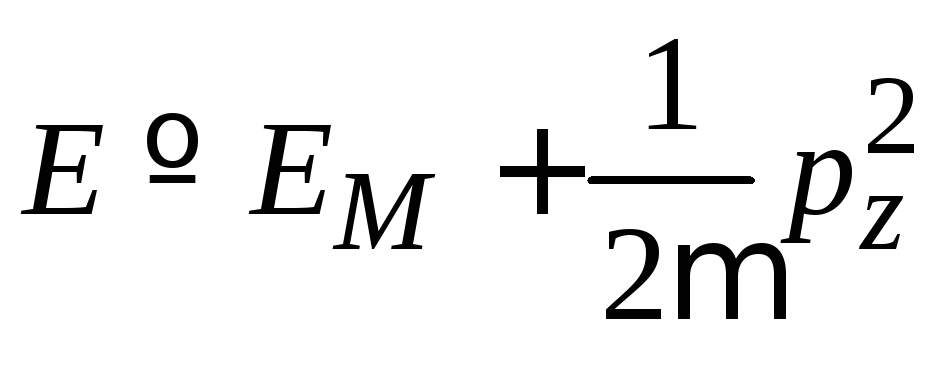Если движение по оси z не ограниченное, то – любое вещественное число.

Уравнение Шредингера получает вид

.

С учетом коммутирующих операторов

, ,

ищем решение в виде произведения собственных функций и

.

Подставляем решение в уравнение, делим его слева на ψ, получаем уравнение для функции

.

Упрощаем уравнение, вводя эффективную потенциальную энергию

,

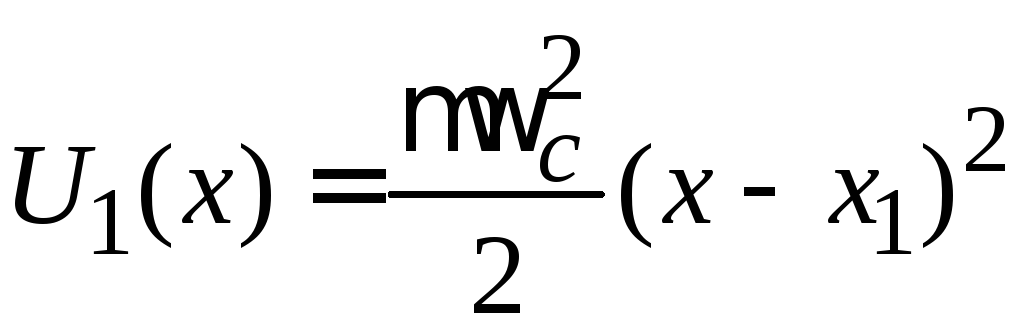аналогичную потенциальной энергии линейного гармонического осциллятора со смещенным положением равновесия, являющимся центром колебаний заряда

. (5.47)

Получаем уравнение

.

Сравниваем с уравнением гармонического осциллятора (3.23)

, ,

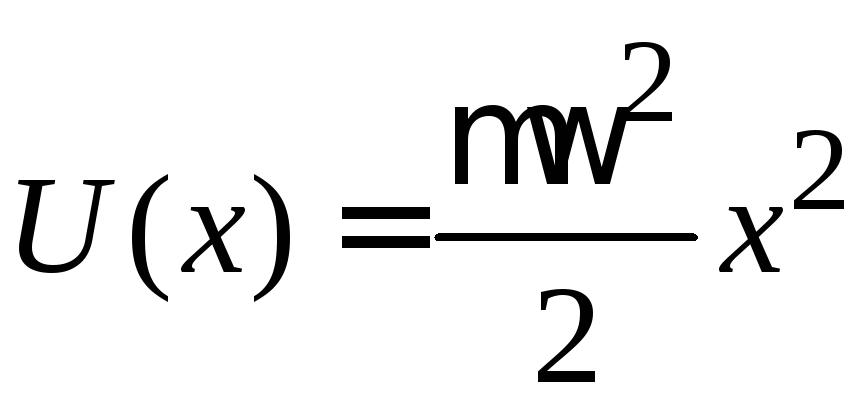колеблющегося с частотой ω и амплитудой нулевых колебаний относительно точки . Задача Ландау соответствует осциллятору, колеблющемуся относительно точкис циклотронной частотой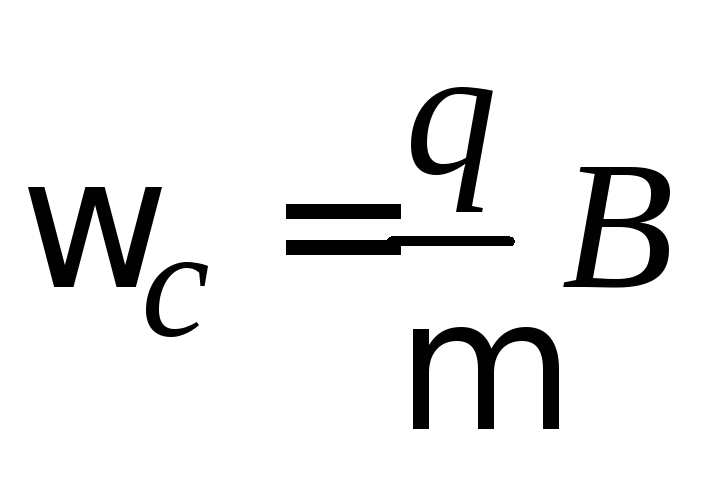и с амплитудой нулевых колебаний, равной магнитной длине:

.

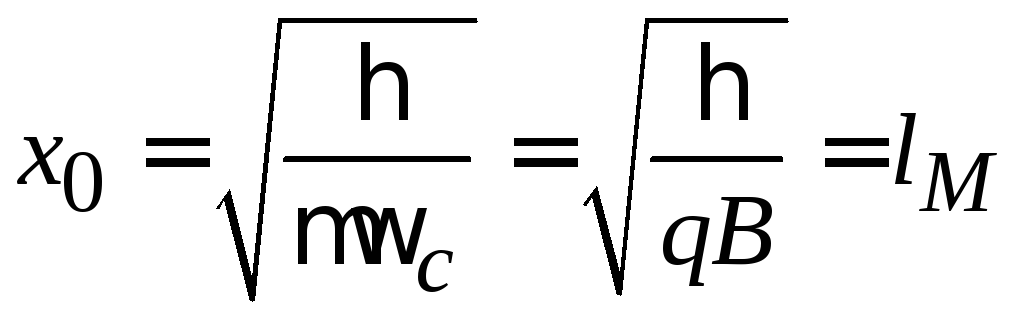Из формулы (3.32) для гармонического осциллятора получаем функцию состояния n

, ,

где – полином Эрмита; n – число нулей волновой функции.

Уровни Ландау. Спектр энергии движения в плоскости , перпендикулярной магнитному полю, совпадает со спектром гармонического осциллятора. Из формулы энергии гармонического осциллятора (3.39) находим

,(5.48)

где – магнетон Бора. Результат согласуется с энергией полуклассической теории с точностью до слагаемого .

Число состояний на уровне Ландау. Функция состояния зависит от положения центра циклотронного движения , энергия (5.48) не зависит от, поэтому уровень Ландау вырожден, то есть разным центрам соответствует одинаковая энергия. Найдем возможное число центров с определенной энергией, то есть кратность вырождения состояния.

Пусть движение заряда ограничено прямоугольной областью со сторонами , . Тогда положение центра находится по осиx в пределах

.

Это ограничивает импульс

интервалом шириной

.

По оси y частица находится в пределах

,

это вызывает квантование импульса . Периодическое граничное условие Борна–Кармана (3.8)

на волновую функцию

требует

.

Учитывая

, N – целое число,

находим

.

Импульс квантуется

,

соседние значения отличаются на шаг

.

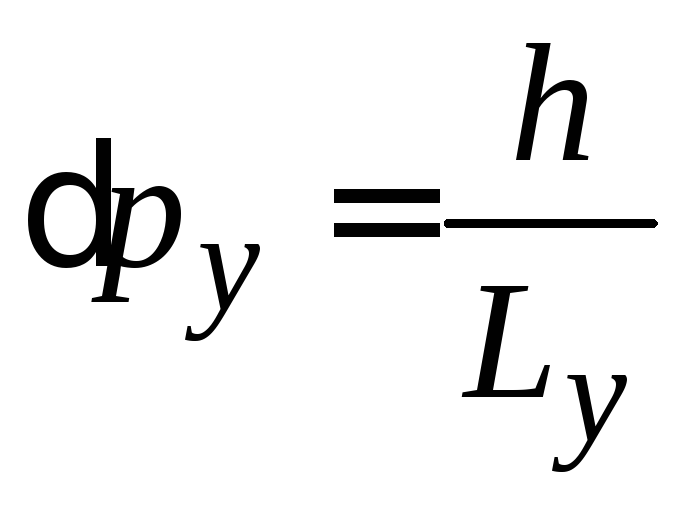Тогда интервал шириной заполняется шагамичислом, и создает вырождение уровня Ландау кратностью

g = (ширина интервала )/(шаг ) =

, (5.52)

где 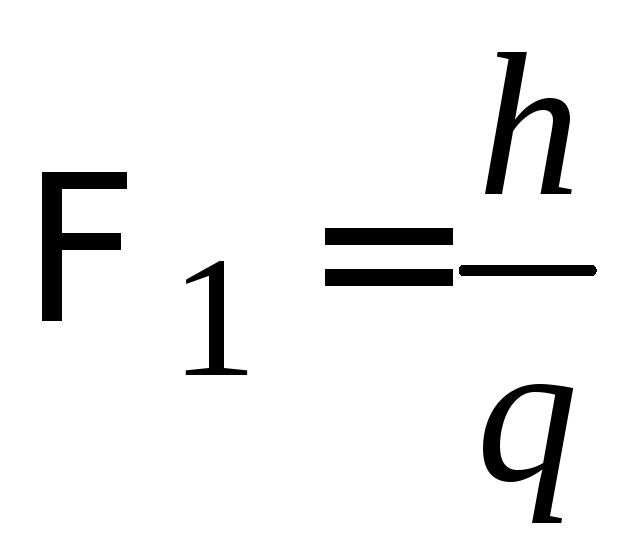–квант магнитного потока. Число состояний на любом уровне Ландау без учета спина равно числу квантов магнитного потока, приходящихся на область, доступную для движения заряда. В полуклассической квантовой механике число квантов магнитного потока равнялось номеру траектории заряда.

Фактор заполнения (filling factor) уровня Ландау показывает число заполненных уровней Ландау

=(поверхностная концентрация электронов)/(кратность вырождения уровня) =

.

В результате

(5.52а)

Квантовый эффект Холла. При заряды в полуклассическом приближении двигаются по орбитам с радиусами (1.29). В двухмерном проводнике с перпендикулярным плоскости магнитным полем при баллистическом движении си при отсутствии рассеяния заряды совершают циклотронные движения и не переносят ток вдоль проводника. Продольная проводимость равна нулю, поперечная проводнику холловская проводимость. Такое явление называетсяцелочисленным квантовым эффектом Холла.