Заряд в магнитном поле

Магнитное поле наряду с электрическим полем широко используется для изменения и контроля состояния электрона. Магнитное поле влияет на фазу волновой функции заряда и на длину волны де Бройля. Это используется для измерения эффективной массы и магнитного момента носителя тока в кристалле, для определения поверхности Ферми и концентрации электронного газа.

Длина волны де Бройля

определяется в магнитном поле не кинетическим импульсом частицы , а полным импульсом, включающим векторный потенциал магнитного поля.

Полный импульс P учитывает влияние магнитного поля на волновую функцию заряда. Пусть магнитное поле создано электрическим полем благодаря явлению электромагнитной индукции, описываемому уравнением Максвелла

,

где А – векторный потенциал, через который выражается индукция магнитного поля

.

Получаем

. (1.18)

Учитываем

,

где  – произвольная скалярная функция, тогда (1.18) выполняется тождественно при

.

Векторный потенциал в классической электродинамике не измерим, его выбор не однозначен. Используем калибровку

,

получаем , в результате

.

Векторный потенциал создает вихревое электрическое поле Фарадея, отличающееся от кулоновского потенциального поля, создаваемого электрическим зарядом, замкнутыми силовыми линиями.

Электрическое поле любой природы действует на заряд q, его кинетический импульс изменяется согласно второму закону Ньютона

.

Интегрируем в пределах от 0 доt и получаем

.

Изменение импульса заряда под действием поля Фарадея за времяt равно

. (1.19)

Определяем полный импульс заряда q

, (1.20)

складывающийся из кинетического импульса частицы

и магнитного импульса, связанного с зарядом q:

.

Согласно (1.19), при изменении векторного потенциала сохраняется полный импульс

.

Ему сопоставляем оператор неизменной формы

. (1.20а)

Оператор имеет собственную функцию в виде плоской волныс фазойи с волновым числом. В результате фаза волновой функции и длина волны де Бройля заряда в магнитном поле определяются полным импульсом, складывающимся из кинетического импульса, зависящего от массы и скорости частицы, и из магнитного импульса, связанного с зарядом частицы и векторным потенциалом поля.

Получим следствия этого результата в рамках полуклассической квантовой механики, а затем с помощью уравнения Шредингера.

Полуклассическое квантование в магнитном поле. В формуле квантования Бора–Зоммерфельда при наличии магнитного поля импульс заменяется полным импульсом

,

. (1.21)

Это условие максимума интерференции при движении заряда в магнитном поле получил Вальтер Франц в 1939 г. Применим результат для частного случая.

Заряд в однородном магнитном поле. Ось z направляем вдоль поля В. На положительный заряд q, движущийся перпендикулярно полю, действует сила Лоренца

,

направленная перпендикулярно полю, скорости V и кинетическому импульсу , по правилу левой руки. Сила, перпендикулярная скорости, являетсяцентростремительной силой, условие равновесия частицы на траектории дает

.

Получаем радиус траектории

. (1.23)

Угловая скорость вращения, или циклотронная частота:

(1.24)

не зависит от скорости заряда.

Для однородного поля В находим векторный потенциал, используя соотношение

,

записанное в цилиндрических координатах

,

,

.

Для рассматриваемого поля

, ,,

получаем

, ,.

Следовательно, вектор А направлен по касательной к траектории заряда и связан с вектором В правилом правого винта. Поле векторного потенциала образует правый вихрь вокруг вектора индукции.

Полный импульс

на круговой траектории с номером , радиусомимеет модуль

. (1.24а)

Вычисляем циркуляции по траектории n составляющих полного импульса

,

.

Результаты подставляем в формулу Бора–Зоммерфельда (1.21)

,

Получаем соотношение между радиусом и импульсом заряда на траектории n

. (1.25)

Квантование импульса и энергии. В (1.25) подставляем (1.23)

,

получаем квантование кинетического импульса и энергии

, (1.26а)

. (1.26б)

Квантовая частица в однородном магнитном поле имеет эквидистантный спектр энергии, совпадающий со спектром гармонического осциллятора, колеблющегося с циклотронной частотой.

Квантование момента импульса. В квантовой механике проекции момента кинетического импульса квантуются

,

Получим квантование проекции момента полного импульса

.

Используем (1.24а)

,

и (1.25)

получаем

. (1.27)

Следовательно, номер траектории n определяется модулем момента полного импульса.

Квантование радиуса траектории. Из (1.23)

выражаем

,

подставляем в (1.26а)

,

получаем квантование радиуса траектории

, (1.29)

где магнитная длина

. (1.30)

Для электрона

нм.

Для магнитного поля у земли

Тл, мкм.

Квантование траекторий электрона в магнитном поле наблюдалось экспериментально в 2012 г. (Phys. Rev. Lett. 109, 116805). Исследовалась пространственная структура двухмерного газа электронов в поверхностном слое полупроводника InSb в магнитном поле В = 6 Тл. Использовался метод сканирующей туннельной спектроскопии. При температуре Т = 0,3 К наблюдались концентрические кольца. Для такого газа из (1.29) и (1.30)

,

,

получаем

нм, нм,нм,нм.

Квантование магнитного потока. Используя (1.29)

,

находим магнитный поток через площадь, ограниченную траекторией:

, (1.31)

где квант магнитного потока

. (1.32)

Согласно (1.31) квантовое число n равно числу квантов магнитного потока, приходящихся на площадь, ограниченную траекторией заряда.

В сверхпроводнике заряд спаренных электронов , тогдаквант магнитного потока в сверхпроводнике

Тл·м² (Вб). (1.33)

Величина Ф₀ приблизительно равна потоку 1/100 магнитного поля земли через площадку диаметром 0,1 мм.

Квантование магнитного потока обосновали В.А. Фок и П. Иордан в 1930 г., Ф. Лондон в 1948 г. Экспериментально явление обнаружили в сверхпроводнике Б. Дивер и В. Фейрбэнк в 1961 г. Слой олова толщиной 0,3 10 мкм гальванически осаждался в виде кольца на кварцевой нити диаметром 13 мкм. При температуре выше сверхпроводящего перехода олова, равного 3,8 К, кольцо помещали в магнитное поле, направленное вдоль оси кольца. Температуру снижали, олово переходило в сверхпроводящее состояние и выталкивало поле из своего объема, создавая поверхностный кольцевой ток и магнитный поток через отверстие кольца. Результат измерений этого потока, где, соответствовал максимуму интерференции для фазы

, (1.34)

образованной волновой функцией куперовской пары с зарядом , проходящей по кольцу.

Квантование сопротивления. Рассмотрим контур с ничтожно малым активным сопротивлением. Плоскость контура пересекает поток магнитного поля Ф. К концам контура приложено напряжение U, по цепи идет ток I. При переносе по замкнутой цепи заряда q источник напряжения совершает работу .

При увеличении магнитного потока на , возникает явление электромагнитной индукции и для поддержания тока источник совершает дополнительную работу. Из закона сохранения энергии получаем

.

В цепи возникает индуктивное сопротивление

. (1.35)

Если ток переносится в сверхпроводнике куперовскими парами электронов с зарядом , то кванту магнитного потока

соответствует квант сопротивления

кОм. (1.36)

Кванту потока с зарядом e

соответствует холловское сопротивление

кОм. (1.36а)

В баллистическом проводнике, где электроны движутся без рассеяния, наблюдается квантование сопротивления

,

где – число активизированных поперечных мод движения, которые дают в продольный ток равные вклады. Результат получил Рольф Ландауэр в 1970 г.

Интерференционные осцилляции сопротивления проводника с двухмерным электронным газом при изменении магнитного поля экспериментально исследовали Юрий Васильевич и Дмитрий Юрьевич Шарвины в 1981 г. Использовалось кольцо из магния диаметром (1,52) мкм. При температуре ~1К длина свободного пробега электронов превышает размер кольца. Электрон движется баллистически без рассеяния, фаза волновой функции меняется упорядоченно. На платиновые контакты А и В подается напряжение. Через кольцо проходит магнитный поток Ф. На контакте А волна де Бройля электрона разделяется и идет по путям 1 и 2, набирая фазы θ₁ и θ₂, и интерферирует на контакте В с разностью фаз .

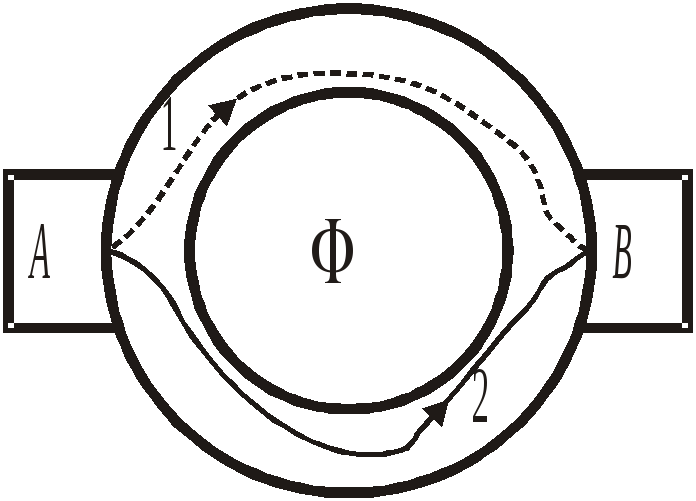
Учитывая, что при обращении движения набираемая фаза меняет знак, можно считать, что электрон делает один оборот по кольцу. Из (1.34)

получаем разность фаз

, .

Изменение магнитного потока на меняет разность фаз на

.

Максимум интерференции соответствует максимуму тока между контактами. В результате при изменении магнитного поля сопротивление между контактами осциллирует с периодом

.

Если через кольцо одновременно переносится заряд , то период осцилляций равен. Эксперимент подтвердил этот вывод.

Квантование магнитного момента. Ток в контуре создает магнитный момент , равный произведению силы токаI на площадь контура S, и направленный перпендикулярно плоскости контура по правилу правого винта.

Электрический ток пропорционален импульсу движущихся зарядов, тогда магнитный момент пропорционален моменту импульса зарядовL

,

где –гиромагнитное отношение, q и μ – заряд и масса частицы, создающей магнитный момент. Используем квантование орбитального момента (1.27)

,

получаем орбитальный магнитный момент электрона

,

, (1.37)

где магнетон Бора

(1.38)

введен В. Паули в 1920 г. Проекция орбитального магнитного момента на направление поля квантуется и пропорциональна магнитному квантовому числу m.

Подстановка импульса. Для описания заряда в электромагнитном поле в рамках квантовой механики используется следующее правило записи гамильтониана частицы – магнитное поле учитывается подстановкой полного импульса, электрическое поле учитывается слагаемым потенциальной энергии.

В магнитном поле длина волны де Бройля определяется полным импульсом . При изменении поля меняется векторный потенциалA и скорость заряда за счет явления электромагнитной индукции, полный импульс сохраняется и ему сопоставляется оператор неизменной формы

. (7.12)

Действие магнитного поля на квантовую систему учитывается подстановкой импульса

. (7.13)

В формулах, описывающих систему без магнитного поля, оператор кинетического импульса заменяется выражением(7.13). Электрическое поле со скалярным потенциалом учитывается дополнительным слагаемым потенциальной энергии

. (7.14)

Операторы физических величин. С учетом замен (7.13) и (7.14) получаем гамильтониан, уравнение Шредингера и плотность тока вероятности для заряда q в электромагнитном поле

, (7.17)

, (7.18)

. (7.19)

Соотношения неопределенностей в магнитном поле. Используя (7.13)

и

, ,,

находим коммутационные соотношения

,

,

. (7.21)

Операторы проекций кинетического импульса заряда в магнитном поле взаимно не коммутируют.

Для операторов скорости

, ,

из (7.21) получаем

,

,

.

Некоммутативность операторов приводит к соотношениям неопределенностей для проекций скорости

,

,

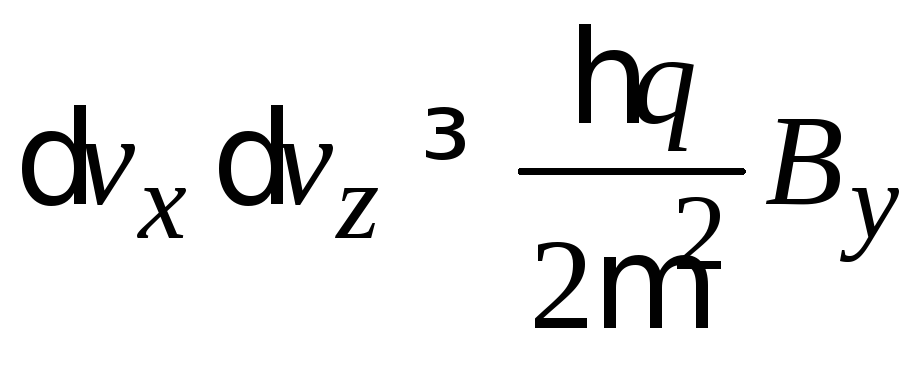. (7.22)

Проекции скорости заряда в магнитном поле определяются одновременно с ограниченной точностью.