Частица в цилиндрической полости

Частица массой μ находится в полости, свободной от полей, радиусом а, длиной образующей s с абсолютно непроницаемыми стенками. Требуется найти уровни энергии и волновые функции частицы. Пример описывает, в частности, атом в углеродной нанотрубке.

Система осесимметричная . Используем цилиндрические координаты с осьюz, совпадающей с осью полости. Из (5.17) получаем общее решение для состояния частицы

.

Используем собственную функцию оператора в виде стоячей волны по осиz

,

и собственную функцию оператора , описывающую равномерное вращение вокруг оси z

,

Радиальная функция удовлетворяет уравнению (5.18)

.

Внутри полости при выполняется, тогда

.

Сравниваем с уравнением Ломмеля

,

получаем параметры

, ,,

Используем общее решение

,

где – функция Бесселя. Учитываем, что цилиндрическая функция Бесселя при инверсии порядка переходит сама в себя с точностью до постоянной фазы

,

тогда общее решение для радиальной функции

.

Краевые условия на торцах непроницаемой полости при и для

имеют вид

,

откуда находим

, ,

Краевое условие на непроницаемой боковой стенке

дает

,

где – корень функции Бесселя ; i – порядковый номер корня. В частности

; ; ; ; ; ; …

В результате получаем спектр значений волнового числа и энергии частицы

, ,

,

где

характеризует скорость движения по оси z;

описывает скорость вращения вокруг оси z;

определяет движение в радиальном направлении.

Основное состояние электрона имеет минимальные значения квантовых чисел: ,,,, и минимальную энергию

.

Водородоподобный атом

В электронной оболочке водородоподобного атома находится один электрон, например . Заряд ядра, гдеZ – порядковый номер элемента в таблице Менделеева. Массивное ядро с Z протонами с учетом его массы считаем неподвижным при движении электрона. Потенциальная энергия электрона

.

Потенциальная энергия и уровни атома водорода

Система центрально-симметричная, используем сферические координаты с центром в ядре. Состояние электрона с энергией E и квантовыми числами l и m описывает волновая функция (5.9)

.

Найдем радиальную функцию и спектр энергии электронаЕ.

Уравнение Шредингера. Для связанного состояния с полной энергией радиальное уравнение (5.10)

получает вид

.

Упрощаем уравнение, переходя к безразмерным величинам. Выражаем энергию через безразмерный параметр

, (5.21)

где боровский радиус атома водорода

. (5.22)

Переходим от радиуса r к безразмерной переменной

, . (5.23)

Для получаем

. (5.24)

Уравнение рассматривалось в курсе “Методы мат. физики”. Нормировка радиальной функции содержит интеграл

,

поэтому необходима его конечность. Если радиальное число

не целое, то решение является бесконечным рядом, и приведет себя как, нормировочный интеграл расходится, такое решение является нефизическим.Сходимость на верхнем пределе интеграла приводит к квантованию

В курсе “Методы мат. физики” получено решение

, (5.25)

где –обобщенный полином Лагерра; .

Квантовые числа. Пространственная и угловая ограниченность движения приводят к дискретности спектра квантовых чисел, характеризующих состояние электрона.

Радиальное число определяет степень полинома, входящего сомножителем в радиальную функцию, равно числу нулей радиальной функции на протяжении .

Главное число

определяет полную энергию электрона. Множество состояний с одинаковым называетсяслоем и обозначается, соответственно: K, L, M, N,…

Орбитальное число l определяет модуль момента импульса электрона. С учетом , находим возможные значения

.

Величина l определяет кинетическую энергию вращения, которая не может быть больше полной энергии, поэтому l ограничена сверху. Множество состояний с одинаковым называетсяоболочкой и обозначается, соответственно: s, p, d, f,…

Магнитное число

определяет проекцию момента импульса электрона. Проекция не может быть больше модуля, поэтому . Число состояний с одинаковымl и разными m, т. е. кратность вырождения по l, равна

.

Основное состояние имеет минимальные значения квантовых чисел: ,,.

Полная энергия. Из (5.21)

с учетом получаем спектр энергии

, (5.26)

где

– энергия основного состояния атома водорода. Энергия не зависит отl и m.

Кратность вырождения состояния n равна числу состояний со всеми возможными l и m при одинаковой энергии и главном числе n. Без учета спина электрона получаем

.

Радиальная функция. В (5.25)

учитываем

, .

Выбрать

,

дает

,

. (5.27)

Обеспечивается нормировка

,

. (5.28)

На малых и на больших расстояниях от ядра выполняется

,

.

Для атома водорода с находим

, ,,;

,

,

–основное состояние,

,

,

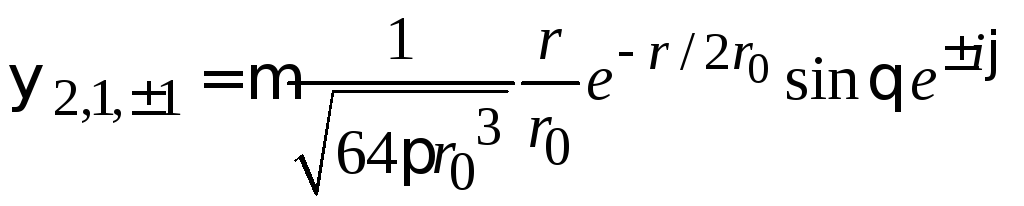. (5.30)

Состояния нормированы

. (5.31)

Плотность вероятности по радиальной переменной равна вероятности обнаружения электрона в шаровом слое радиусом r толщиной

, (5.32)

где

– вероятность обнаружения электрона в шаровом слое радиусом r, толщиной dr; объемом

.

Для состояния находим. Учитывая, из (5.27)

, ,

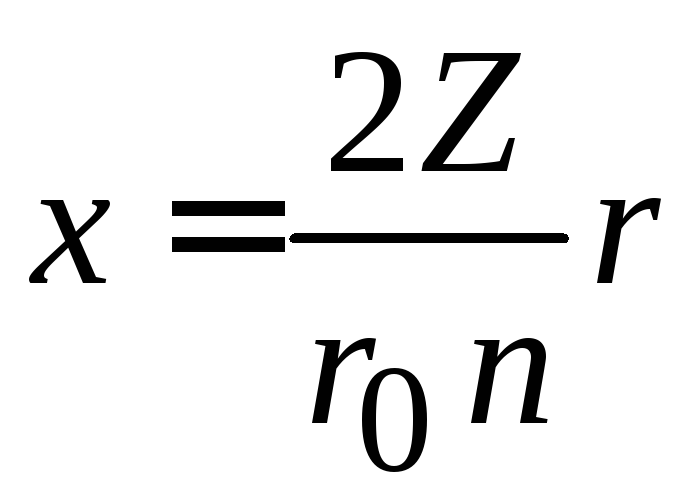для атома водорода получаем состояния с нулевым радиальным числом

.

Положение максимума плотности вероятности следует из условия

,

находим

. (5.33)

Для ,получаем–максимум плотности вероятности основного состояния находится на расстоянии r₀ от ядра, что оправдывает его название – боровский радиус атома водорода.

Плотность вероятности состояния 1s

Орбиталь – область наиболее вероятного нахождения электрона в атоме в координатах , где угол θ отсчитывается от осиz. Плотность изображения на рисунке пропорциональна модулю волновой функции

.

Показаны результаты для ;;.

l = 0 1 2 n =

Орбитали атома водорода

Радиальная структура усложняется с ростом n, угловая структура усложняется с увеличением l.

Экситон (от лат. excito – «возбуждаю») является связанным состоянием электрона e и дырки h с эффективными массами ив полупроводнике. Существование экситона предсказал Френкель в 1931 г.

Яков Ильич Френкель (1911–2000)

Экситон возникает в полупроводнике при низкой температуре в результате поглощения фотона. При повышении температуры экситон разрушается тепловым движением. Энергия фотона разрывает кристаллическую связь, появляются свободный электрон и дырка. Центр масс экситона описывается радиус-вектором

,

где – полная масса. Относительное положение квазичастиц характеризует

.

Кинетическая энергия экситона складывается из движения центра масс и относительного движения электрона и дырки

,

где –приведенная масса. В системе центра масс экситон описывается как частица, находящаяся в среде с относительной диэлектрической проницаемостью , в кулоновском поле

.

Экситон Ванье–Мотта аналогичен водородоподобному атому с большим боровским радиусом

и с малой полной энергией

.

Переходы между такими состояниями в оксиде меди при температуре жидкого азота наблюдал Е.Ф. Гросс в 1952 г.

Следовательно, электрон и дырка экситона находятся относительно далеко друг от друга на расстояниях, превышающих 10d, где d – постоянная решетки, и образуют связанное состояние с малой энергией. В тонких пленках экситон существует при комнатных температурах. Экситоны используются в электрооптических преобразователях.

Евгений Федорович Гросс (1897–1972)

Ридберговский атом имеет высокоэнергетическое состояние электрона с квантовыми числами . Фотоны лазера переводят электрон последовательно с основного на болеевысокие уровни энергии. Далее электрон локализуют, создавая волновой пакет путем кратковременного облучения атома микроволновым излучением. К такому состоянию применима полуклассическая теория атома Бора. Ридберговский атом достигает макроскопических размеров. Получены возбужденные состояния атома калия с диаметром траектории электрона ~1 мм, что соответствует главному квантовому числу . Частоты переходов между соседними состояниями с большими квантовыми числами находятся в микроволновой области, а не в оптической, как для низко возбужденных состояний. Электрический дипольный момент атома пропорционален его размеру, поэтому велика энергия взаимодействия атома с внешним электрическим полем и таким атомом легко манипулировать. Время существования ридберговского атома.