Блочный алгоритм мнк в частотной области

Выходной сигнал адаптивного КИХ - фильтра - это линейная свертка входного сигнала x[k] и импульсной характеристикиh[k] , гдеL_B– длина импульсной характеристики фильтра. В курсе «Теория и обработка сигналов» было показано, вычисление свертки выполняется значительно быстрее в частотной области за счет использования алгоритма БПФ.

Свертке в частотной области соответствует произведение преобразований Фурье, т.е.- свойство свертки ДВПФ. Такая свертка являетсяпериодической с периодом L, где L – размер ДПФ. Этот метод вычисления называют круговой (быстрой) сверткой. Благодаря БПФ вычисление свертки в частотной области требует операций умножений вместоL². Чем больше длина L, тем быстрее вычисляется круговая свертка. Вычисление ДПФ требует блочного использования данных. Наиболее часто при этом используется метод наложения – сложения вычисления свертки (Overlap-and-Add Method).

В MATLAB для реализации блочного метода адаптивной фильтрации в частотной области служит специальная функция ha=adaptfilt.blmsfft(l,step,leakage,blocklen,coeffs,states).

Она аналогична использовавшейся выше функции

ha = adaptfilt.blms(l,step,leakage,blocklen,coeffs,states), но в отличие от неё длина length(blocklen) и length(coeffs) должна быть равна степени два (=2^M). Если выполняется данное условие длины, то будет использоваться блочная функция с вычислениями в частотной области. Кроме того, длина входного сигнала должна делиться нацело на длину блока. Такие ограничения алгоритма.

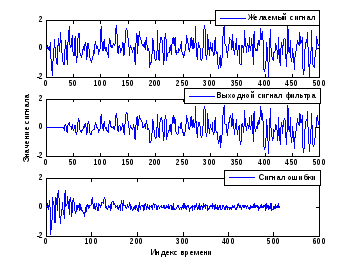
Ниже приведены результаты моделирования задачи идентификации системы 16-го порядка, аналогичные предыдущему примеру, но в данном случае используется функция adaptfilt.blmsfft(), длина входного сигнала фильтра выбрана равной 512 отсчетов и длина блока данных - 32 отсчета. Программа размещена в Приложении 6.

Вычислительная сложность блочного алгоритма МНК в частотной области примерно равна сложности блочного алгоритма, приведенной выше.

Приложение 1. Пример адаптивной фильтрации с использованием метода НМНК

% адаптивная фильтрация - алгоритмы МНК и нормализованный МНК

k=(1:1000)';

s=sin(0.1*pi*k); % полезный гармонический сигнал

f1=[1, 0.6]; % БИХ - фильтр для получения шума на опорном входе

n=1.5*randn(1000,1);

n1=filter(1,f1,n); % шум на опорном (желаемом) входе

d=s+n1; % сигнал с шумом на опорном входе

f2=[1, -0.5, 0.6, -0.2]; % КИХ - фильтр для шума на основном входе

x=filter(f2, 1, n); % шум на основном входе

N=10; % число коэффициентов адаптивного фильтра

Hlms=adaptfilt.lms(N); % конструирование адаптивного фильтра

Hnlms=adaptfilt.nlms(N);

% определение максимального размера шага

[mumaxlms,mumaxmselms] = maxstep(Hlms,x);

Hlms.StepSize = mumaxmselms/20; % установка размера шага

[mumaxnlms,mumaxmsenlms] = maxstep(Hnlms);

hnlms.StepSize = mumaxmsenlms/20;

fwin=firwiener(N-1,x,d); % реализация фильтра Винера

ywin=filter(fwin,1,x); % фильтрация фильтром Винера

ewin=d-ywin; % получение оценки полезного сигнала ф_ром Винера

Hlms = adaptfilt.lms(N,Hlms.StepSize); % получение фильтра МНК

[ylms,elms] = filter(Hlms,x,d);% Фильтрация стандартным МНК

Hnlms = adaptfilt.nlms(N,hnlms.StepSize); % получение нормализованного фильтра

[ynlms,enlms] = filter(Hnlms,x,d); % фильтрация нормированным МНК

% построение графиков сигналов

subplot(311)

plot(k(800:end),d(800:end),k(800:end),s(800:end))

legend('Сигнал с шумом','Сигнал')

subplot(312)

plot(k(1:200), ewin(1:200),k(1:200),elms(1:200),k(1:200),enlms(1:200));

legend('Фильтр Винера','Фильтр МНК', 'Фильтр НМНК')

ylim([-3 3]);

subplot(313)

plot(k(800:end), ewin(800:end),k(800:end),elms(800:end),k(800:end),enlms(800:end));

xlabel('Индекс времени (к)'), ylabel('Уровень сигнала')

Приложение 2.

% Моделирование задачи идентификации

% КИХ - системы

K = 50; % Число усредняемых реализаций

x = zeros(2000,K);

d = x; % Инициализация переменных

h = fir1(31,0.5); % КИХ - система для идентификации

% Это оконный фильтр 31-го порядка с частотой среза 0,5

x = filter(1,[1 -0.5],sign(randn(size(x))));

n = 0.1*randn(size(x)); % случайный шум

d = filter(h,1,x)+n; % желаемый сигнал

L =32; % длина адаптивного фильтра

mu1 = 0.005; % размер шага сходимости

mu2 = 0.9;

M = 10; % коэффициент прореживания отсчетов

h1 = adaptfilt.lms(L,mu1);

h2 = adaptfilt.nlms(L,mu2);

[mse1,meanH1,Hsim1,traceKsim1] = msesim(h1,x,d,M);

[mse2,meanH2,Hsim2,traceKsim2] = msesim(h2,x,d,M);

nn = M:M:size(x,1);

subplot(1,2,1);

semilogy(nn,mse1);

title(' Кривая обучения МНК ');

xlim([0 size(x,1)])

%legend('Измеренная MSE');

xlabel('индекс времени'); ylabel('значение средней квадратичной ошибки');

subplot(1,2,2);

semilogy(nn,mse2);

title(' Кривая обучения нормированного МНК ');

xlim([0 size(x,1)])

xlabel('индекс времени'); ylabel('значение средней квадратичной ошибки');

Приложение 3

K = 20; % Число усредняемых реализаций

x = zeros(2000,K);

d = x; % Инициализация переменных

h = fir1(31,0.5); % КИХ - система для идентификации

% Это оконный фильтр 31-го порядка с частотой среза 0,5

x = filter(1,[1 -0.5],sign(randn(size(x))));

n = 0.1*randn(size(x)); % случайный шум

d = filter(h,1,x)+n; % желаемый сигнал

L =32; % длина адаптивного фильтра

M = 10; % коэффициент прореживания отсчетов

mu = 0.005; % значение шага сходимости

h0 = adaptfilt.lms(L,mu);

[mse0,meanH0,Hsim0,traceKsim0] = msesim(h0,x,d,M);

h1 = adaptfilt.se(32,mu);

[mse1,meanH1,Hsim1,traceKsim1] = msesim(h1,x,d,M);

h2 = adaptfilt.sd(32,mu);

[mse2,meanH2,Hsim2,traceKsim2] = msesim(h2,x,d,M);

h3 = adaptfilt.ss(32,mu);

[mse3,meanH3,Hsim3,traceKsim3] = msesim(h3,x,d,M);

nn = M:M:size(x,1);

subplot(4,1,1), semilogy(nn,mse0);

legend(' кривая обучения МНК '); axis([0 size(x,1) 0.0001 1]);

ylabel('СКО');

subplot(4,1,2), semilogy(nn,mse1);

legend(' кривая обучения алгоритма знака ошибки '); axis([0 size(x,1) 0.0001 1]);

ylabel('СКО');

subplot(4,1,3), semilogy(nn,mse2);

legend(' кривая обучения алгоритма знака сигнала '); axis([0 size(x,1) 0.0001 1]);

ylabel(' СКО');

subplot(4,1,4), semilogy(nn,mse3);

legend(' кривая обучения алгоритма двойного знака '); axis([0 size(x,1) 0.0001 1]);

xlabel('индекс времени'), ylabel('СКО');

Приложение 4.

% Задача идентификации КИХ - фильтра 15 - го порядка

x = randn(1,500); % Входной сигнал фильтра

b = fir1(15,0.5); % КИХ - фильтр для идентификации

no = 0.1*randn(1,500); % Дополнительный шум

d = filter(b,1,x)+no; % Желаемый сигнал

mu = 0.008; % Шаг сходимости

n = 10; % Размер блока

ha = adaptfilt.blms(16,mu,1,n); % конструирование фильтра

[y,e] = filter(ha,x,d); % фильтрация

subplot(3,1,1); plot(1:500,[d;y;e]);

title(' Идентификация системы');

legend('Желаемый сигнал','Выходной','Ошибка');

xlabel('Индекс времени'); ylabel('Значения сигнала');

subplot(3,1,2); stem(b);

legend('Исходный фильтр');

subplot(3,1,3); stem([ha.coefficients]);

legend('Коэффициенты адаптивного фильтра');

xlabel('Номер коэффициента'); ylabel('Значение коэффициента');

grid on;

Приложение 5

% Модель задачи адаптивного подавления акустического шума

s=wavread('dspafxf_8000.wav'); % исходный сигнал- от микрофона 1

Fs = 8000; % частота отсчетов

k=1:length(s);

n1=1.5*randn(length(s),1); % высокочастотный шум

b=fir1(39, .25);

n=filter(b,1,n1);% шум - от микрофона 2

x=s+n; % сигнал плюс шум

N=40; % число коэффициентов фильтра

Hnlms=adaptfilt.nlms(N);% конструирование адаптивного фильтра

% определение максимального размера шага

[mumaxnlms,mumaxmsenlms] = maxstep(Hnlms);

hnlms.StepSize = mumaxmsenlms/40;

Hnlms = adaptfilt.nlms(N,hnlms.StepSize); % получение нормализованного фильтра

[ynlms,enlms] = filter(Hnlms,x,n); % фильтрация нормированным МНК

figure(1)

subplot(411), plot(k/Fs, s), title(' Аудиосигнал')

subplot(412), plot(k/Fs, n ); title('Шум')

subplot(413), plot(k/Fs, x ); title('Сигнал + Шум')

subplot(414), plot(k/Fs, enlms );

ylim([-1, 1]);

title(' Очищенный выходной сигнал - ошибка фильтра')

xlabel('Время, с')

% Прослушивание сигналов

wavwrite(s,'file_s');

y1=wavread('file_s');

sound(y1,8000);

wavwrite(enlms,'file_x');

y2=wavread('file_x');

sound(y2,8000);

wavwrite(enlms,'file_enlms');

y3=wavread('file_enlms');

sound(y3,8000);

Приложение 6

x = randn(1,512); % Вход фильтра

b = fir1(16,0.5); % Система для идентификации

no = 0.1*randn(1,512); % Внешний шум

d = filter(b,1,x)+no; % Желаемый сигнал

mu = 0.01; % Размер шага сходимости

n = 32; % Длина блока

ha = adaptfilt.blmsfft(16,mu,1,n);

[y,e] = filter(ha,x,d);

subplot(3,1,1); plot(1:500,d(1:500));

legend('Желаемый сигнал')

subplot(3,1,2); plot(1:500,y(1:500))

ylabel('Значение сигнала');

legend('Выходной сигнал фильтра')

subplot(3,1,3); plot(e)

legend(' Сигнал ошибки')

xlabel('Индекс времени');

figure(2)

subplot(2,1,1); stem(b')

grid on

legend('Коэффициенты системы')

subplot(2,1,2); stem(ha.coefficients')

legend('Коэффициенты адаптивного фильтра')

xlabel('Номер коэффициента');

ylabel('Значение коэффициента');

grid on;