

В методе наименьших квадратов (МНК) и
его вариантах, рассмотренных в предыдущих
лекциях курса, цель работы АФ заключается
в минимизации среднеквадратичной
ошибки фильтра
При этом новые значения коэффициентов
адаптивного КИХ – фильтра вычисляются
по выражению
Другой подход лежит в основе второго
популярного метода адаптивной
фильтрации сигналов - рекурсивного
алгоритма наименьших квадратов (РМНК,
англ. RLS). В этом подходе в любой момент
времени k >
0 параметры адаптивного фильтра
вычисляются таким образом, чтобы
минимизировать величину суммы квадратов
ошибок
в которой
При этом сама структура фильтра
остается прежней, изменяется только
алгоритм адаптацииИсходная формулировка алгоритма наименьших квадратов
![]() .
.![]() .
.![]() ,
,![]() -
это значения ошибки фильтра для моментов
времениs=1,2,…,k,
-
это значения ошибки фильтра для моментов
времениs=1,2,…,k,![]() - весовые коэффициенты ошибки,
предназначенные для уменьшения влияния
прошлых значений ошибок по сравнению
с текущими.
- весовые коэффициенты ошибки,
предназначенные для уменьшения влияния
прошлых значений ошибок по сравнению
с текущими.

Для большей ясности методу РМНК можно
дать такую интерпретацию.
Предположим, что желаемый сигнал d
на основном входе фильтра
представляет собой некоторую желаемую
кривую (функцию). Значения (отсчеты) на
выходе адаптивного фильтраyk- это другая последовательность,
связанная с входным сигналомxk
регрессионной зависимостью
(уравнением)
в которой X- входной
сигнал фильтра ,h[i]– оцениваемые по уравнению регрессии
коэффициенты фильтра H,ek-значения случайной ошибки фильтра,
независимые (важное предположение!) от
входного сигнала.
В таком подходе задача выбора коэффициентов
фильтра h[i]может рассматриваться как типичная
задача метода наименьших квадратов
или задача сглаживания методом
наименьших квадратов. Наилучшим
приближением сигналаd
на выходе фильтра будет такая
функцияy , которая минимизирует
сумму квадратов разностей (ошибок)
между кривымиdиy.
Вектор значений ошибок
![]() ,
, ,
,
Здесь Xk –
матрица входного сигнала размером
[k+1]xN,т.е.
Это разреженная матрица, в которой
элементы выше главной диагонали –
нули.
При этом сумма квадратов ошибок
Для минимизации ошибки
В принципе по этому выражению можно
на каждом очередном шаге пересчитывать
коэффициенты фильтра Hopt,
но размер матрицы
Поэтому в адаптивной фильтрации этот
метод не применяется. Используется
специальный рекурсивный алгоритм
вычисления
Эта разновидность алгоритма называется
рекурсивным МНК (РМНК).
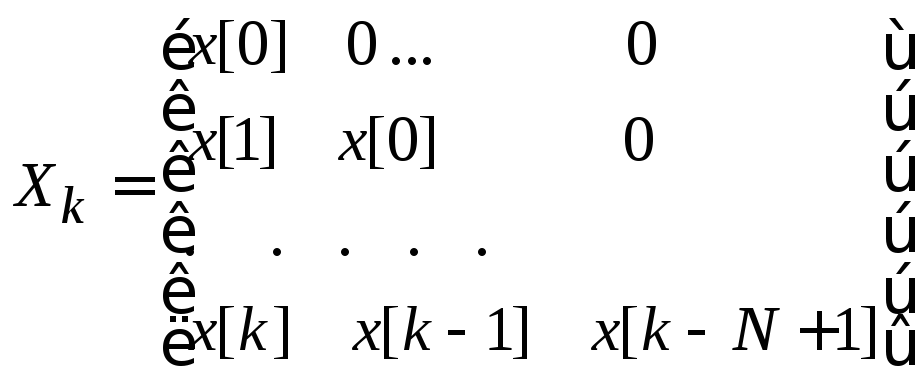 .
.![]()
![]() нужно найти её производную поHи
приравнять нулю для получения оптимальных
значений коэффициентовHopt. При
этом получим известное уравнение
линейной регрессии в матричной форме
нужно найти её производную поHи
приравнять нулю для получения оптимальных
значений коэффициентовHopt. При
этом получим известное уравнение
линейной регрессии в матричной форме![]()
![]() на каждом новом шагеkувеличивается, т.к. поступают новые
значения (точки) сигналаx. При
этом каждый раз нужно заново вычислять
обратную матрицу
на каждом новом шагеkувеличивается, т.к. поступают новые
значения (точки) сигналаx. При
этом каждый раз нужно заново вычислять
обратную матрицу![]() .
Напомним, что вычисление обратной
матрицы очень трудоемкая в вычислительном
отношении процедура с порядком числа
операцийN3.
.
Напомним, что вычисление обратной
матрицы очень трудоемкая в вычислительном
отношении процедура с порядком числа
операцийN3.![]() .
В результате предыдущие значения
коэффициентов фильтра рекурсивно
уточняются на очередном шаге.
.
В результате предыдущие значения
коэффициентов фильтра рекурсивно
уточняются на очередном шаге.
