Алгоритмизированные задания по курсу ТОЭ / Конец

3.3. Расчет токов символическим методом

Данный расчет можно проводить без «развязки» индуктивных связей по уравнениям (5). Однако расчет рассматриваемой цепи может быть существенно упрощен, если воспользоваться «развязкой» индуктивно связанных элементов. При «развязке» индуктивных связей не принимается во внимание: согласно или встречно включены катушки. Ориентируются лишь на расположение одноименных зажимов магнитно-связанных катушек относительно узла, к которому они присоединены. Правило развязки: две индуктивно-связанные катушки, присоединенные к какому-либо узлу непосредственно (узел 1 на рис. 21), после «развязки» подключаются к этому же узлу 1 через промежуточную звезду сопротивлений

а

б

Рис. 21

Если одноименные зажимы магнитно-связанных катушек одинаково ориентированны по отношению к узлу, к которому они подсоединены, то при развязке связей в ветви с индуктивно-связанными катушками включаются реактивные сопротивления , а в общую ветвь, исходящую из узла 1, включается сопротивление , и наоборот. Рис. 21,а,б иллюстрирует «развязку» магнитных связей для обоих случаев.

В результате развязки магнитных связей схема рис.20 принимает вид, показанный на рис. 22.

Рис. 22

Наиболее просто полученная схема рассчитывается методом узловых потенциалов. Если принять потенциал ₀ равным нулю, то уравнение для узла «0₁» по методу узловых потенциалов будет иметь вид:

,

где Z₁, Z₂, Z₃ - комплексные сопротивления отдельных ветвей схемы (рис. 22):

,

,

.

Определив потенциал узла «0₁», можно рассчитать комплексы токов в ветвях схемы (рис. 22), используя закон Ома:

, ,

.

Перед расчетом рекомендуется схему (рис. 22) привести к виду, показанному на рис. 23, объединив в каждой ветви последовательно соединенные сопротивления в одно эквивалентное. При расчете символическим методом все операции осуществляются в комплексной форме (см. приложение 3).

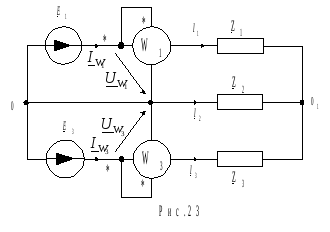
Рис. 23

3.4. Баланс мощности

Баланс полной мощности в комплексной форме представляется в виде

,

где – суммарная комплексная мощность источников ЭДС; – суммарная мощность потребителей; и – комплексы напряжения и тока в комплексном сопротивлении Z_n; – сопряженный комплекс тока, I_n – действующее значение тока (модуль комплексного тока).

Комплексные мощности источников и потребителей рекомендуется представить в алгебраической форме записи для оценки их активных и реактивных составляющих .

Показания ваттметров следует определять по выражению или , где – комплексное напряжение на обмотке напряжения ваттметра; – сопряженный комплексный ток, протекающий по токовой обмотке ваттметра.

Примечание. P_W  0, если ток I_W втекает в генераторный зажим токовой обмотки ваттметра (обозначен «*»), а напряжение U_W направлено от генераторного зажима обмотки напряжения ваттметра.

3.5. Построение круговой диаграммы

В ряде практических случаев представляет интерес характер изменения тока или напряжения на некотором участке цепи, при изменении параметров какого-либо элемента в схеме. Наряду с аналитическим такая задача имеет графическое решение. Сущность этого решения заключается в построении геометрических мест концов векторов напряжения или тока. Полученные кривые называют годографами. Частным случаем годографа является круговая диаграмма, когда варьируемый параметр изменяется только по модулю.

В соответствии с индивидуальной карточкой задания (рис. 16) требуется построить круговую диаграмму для тока I₃ при изменении величины емкости конденсатора С₂ от нуля до бесконечности, что фактически означает изменение модуля комплексного сопротивления в пределах от бесконечности до нуля. Для удобств дальнейших рассуждений выделим из комплексного сопротивления Z₂ второй ветви (см. рис. 23) элемент с переменным параметром (конденсатор С₂, перечеркнутый стрелкой). Полученная при этом схема (без учета ваттметров) представлена на рис. 24. В этой схеме:

,

,

,

.

Рис. 24

Выражение для тока I₃ представляется в виде дуги окружности в комплексной форме записи:

,

где I_3x – ток в третьей ветви при ; I_3к – ток в третьей ветви при ; – модуль входного комплексного сопротивления схемы относительно элемента с переменным параметром (в рассматриваемом примере относительно конденсатора С₂ с переменной емкостью); φ_вх – аргумент входного сопротивления; – модуль изменяющегося комплексного сопротивления, φ₂ – аргумент переменного комплексного сопротивления (в рассматриваемом примере φ₂ = –90º).

Примечание. Токи частных режимов I_3x и I_3к должны иметь тоже направление, что и реальный ток I₃.

3.5.1. Определение тока I_3x (при переменном сопротивлении ).

Схема для этого режима представлена на рис. 25.

Рис. 25 Рис. 26

Как следует из схемы,

.

3.5.2. Определение тока I_3к (при переменном сопротивлении ).

Схема для этого режима представлена на рис. 26. Ток I_3к можно определить по методу узловых потенциалов. Если принять потенциал ₀ равным нулю, то уравнение для узла «0₁» по методу узловых потенциалов будет иметь вид:

,

Определив потенциал узла «0₁», можно рассчитать комплекс искомого тока, используя закон Ома:

.

3.5.3. Определение входного сопротивления цепи относительно переменного элемента.

Для оценки входного сопротивления рассматриваемая цепь делается пассивной (для чего все источники ЭДС закорачиваются). Полученная при этом схема представлена на рис. 27.

Рис. 27

Как следует из схемы, входное сопротивление относительно точек «а» и «б», к которым подключается переменное сопротивление, определится соотношением:

.

3.5.4. Построение круговой диаграммы для тока I₃.

Построение круговой диаграммы проиллюстрировано на (рис. 2 8).

Порядок построения:

 произвольно выбираются масштабы тока и сопротивления (m_I и m_Z);

 на комплексной плоскости в выбранном масштабе изображаются векторы I_3к и I_3x. Разность (I_3к – I_3x) является хордой (О₁К) искомой окружности;

 на самой хорде или на ее продолжении в выбранном масштабе откладывается отрезок О₁А, соответствующий ;

 из точки “А” под углом (_вх-₂) к вектору О₁К проводится линия переменного параметра AN^/ (в рассматриваемой иллюстрации полагается, что (_вх-₂)  0) ;

Рис. 28

 к середине хорды О₁К восстанавливается перпендикуляр;

 из начала хорды О₁К проводится перпендикуляр к линии переменного параметра или к ее продолжению. Центр окружности лежит в точке пересечения этих двух перпендикуляров (точка С).

– Рабочая часть окружности расположена по ту же сторону от хорды, что и линия переменного параметра.

– В масштабе параметра на линии переменного параметра откладывается отрезок AN₁, являющийся модулем переменного сопротивления .

– Из начала хорды (точка О₁) через точку N₁ проводится прямая.

– Точка пересечения этой прямой с дугой окружности определяет конец вектора I₃ (точка М).

В соответствии с заданием по круговой диаграмме определить максимальное и минимальное значения тока в третьей ветви, а также найти этот ток для случая, когда значение меняющегося сопротивления равно его значению при расчете токов символическим методом в пункте 3 задания.

Литература

1. Зевеке Г.В., Ионкин П.А. Основы теории цепей. – М.: Энергия, 1989.

2. Атабеков Г.И. Линейные электрические цепи. – Ч.1. – М.:Энергия,1978.

3. Бессонов Л.А. Теоретические основы электротехники. – Ч. 5. – М.: Высшая школа, 1973.

4. Ионкин П.А. Теоретические основы электротехники. – Т.1. – М.: Высшая школа, 1976.

5. Каплянский А.Е. Теоретические основы электротехники. – М.: Высшая школа, 1972.

6. Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники. – Ч.2. – М.: Энергии, 1981.

36