25.1. Частотное управление эмпирической модовой декомпозицией сигналов

Модель сигнала. Для рассмотрения процесса OEMD зададим (рис. 25.1.1) математическую модель зашумленного сигнала f_k с локальными нестационарными частотными составляющими (сигналами) f1_k – f4_k, которые в сумме образуют полезную информацию f0_k и которые необходимо выделить из сигнала в раздельной форме. Мощность шумов соизмерима с мощностью локальных сигналов.

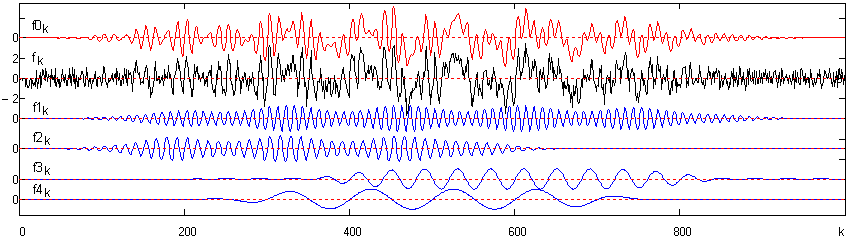
Рис. 25.1.1. Математическая модель сигнала.

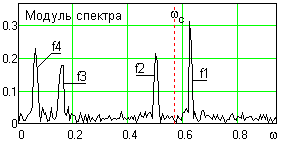
Локальные сигналы представляет собой радиоимпульсы с несущими частотами -, два первых из которых амплитудно-модулированы. Белый шум постоянной мощности распределен по всему частотному диапазону сигнала. Амплитудно-частотная характеристика (АЧХ) сигнала f_k (модуль частотного спектра в правой части главного частотного диапазона) приведена на рис. 25.1.2. Здесь и в дальнейшем для перевода функций в частотную область представления используется быстрое преобразование Фурье (БПФ).

Рис. 25.1.2. Амплитудно-частотный спектр

модельного сигнала

Условия очистки. В принципе, когда сигнал не зашумлен и в спектре сигнала хорошо выделяются все частотные составляющие (а равно и при априорно известном частотном составе полезной информации), нет необходимости в применении EMD. Разделение частотных компонент может быть выполнено полосовыми частотными фильтрами. Однако для произвольных сигналов при наличии шумов, в спектре сигнала можно уверенно идентифицировать только главные несущие частоты, а все нестационарности сигнала и боковые модуляционные частоты маскируются шумом.

На результаты EMD влияет также отношение мощности шумов к мощности сигнала. Увеличение мощности шумов вызывает «дробление» и искажение даже монотональных функций IMF, т.к. частотные составляющие шума влияют на процесс отсеивания EMD, и на отдельных временных (координатных) интервалах возникает процесс «просачивания» из соответствующих масштабных функций IMF части главных частот на соседние IMF. При близких несущих частотах стандартное EMD может не разделять радиоимпульсы и отсеивать их в одну IMF даже при анализе чистых сигналов. В зашумленных сигналах может наблюдаться искажение всех локальных составляющих, о чем наглядно свидетельствует EMD сигнала f_k на рис. 25.1.3.

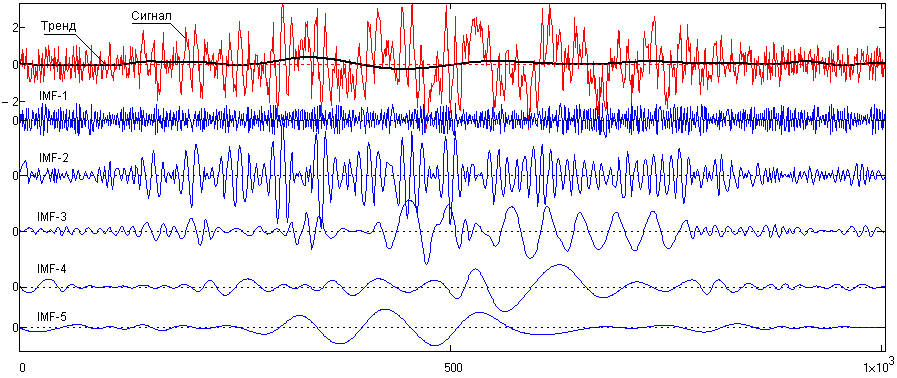
Рис. 25.1.3. Стандартное EMD модельного сигнала

Принцип управления EMD. Для разделения радиоимпульсов в различные IMF необходимо вмешаться в процесс EMD, что можно выполнить с использованием априорной информации о спектральном составе сигналов или непосредственно по оперативной информации о спектре сигнала и спектрах выделяемых IMF.

С учетом следования уровней IMF от высоких частот к низким, на первый уровень в IMF-1 отделяются высокочастотные шумы сигнала за пределами высоких частот полезной информации, что будет рассмотрено ниже. На второй уровень в IMF-2 в принятой нами модели сигнала необходимо отделить сигнал f1. Для этого низкочастотным НЧ-фильтром с граничной частотой среза _c ниже частот радиоимпульса f1 (рис. 25.1.2) отфильтруем все частоты сигнала в интервале 0-_c и используем результат в качестве начальной функции итераций выделения второй IMF [1]. Аналогично на следующий уровень IMF может быть отсеян радиоимпульс f2, и т.д.

Оценка качества. На модельном сигнале оценку качества разделения сигналов можно проводить вычислением коэффициента взаимной корреляции () между информационными функциями и их IMF-образами или угла расхождения векторов (vectors divergence angle - VDA)  = argcos  этих функций. Наиболее удобным для сравнения различных вариантов можно считать параметр VDA, который имеет линейный характер изменения своих значений от 0^о при полном совпадении функций до 90^о при их полной ортогональности (нулевой корреляции).

В этом и заключается сущность частотного управления процессом EMD (метод OEMD), эффективность которого исследуем ниже.