
- •Оглавление
- •Введение
- •1. Математические основы цос
- •2. Z-преобразование
- •3. Структурные схемы и разностные уравнения лис-цепей
- •4. Случайные последовательности и лис-цепи
- •5. Многомерные последовательности и лис-цепи
- •6. Синтез цифровых фильтров
- •7. Взаимосвязь аналоговых, дискретных и цифровых сигналов
- •8. Реализация цифровых фильтров
- •9. Сигнальные процессоры и их применение
- •10. Расчетно-графические задания Задание 1
- •Задание 2
- •Справочный материал
- •10. Геометрическая прогрессия
- •Литература
Министерство образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
––––––––––––––––––––––––––––––––––––––––––––––––––––––––
В.Н. ВАСЮКОВ, Д.В. ГОЛЕЩИХИН
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
Сборник задач и упражнений
для студентов вузов
Новосибирск
2004
УДК 621.372.083.92 (076.1)
В 201
Рецензент: д-р техн. наук, проф. А.Г. Вострецов
Работа подготовлена на кафедре теоретических основ
радиотехники НГТУ
Васюков В.Н., Голещихин Д.В.
В 201 Цифровая обработка сигналов: Сборник задач и упраж-
нений для студентов вузов. – Новосибирск: Изд-во НГТУ,
2004. – 40 с.
Сборник содержит задачи и упражнения по цифровой обработке сигналов.
Сборник предназначен для студентов вузов, обучающихся
по направлению 552500 – «Радиотехника» и специальности
201200 – «Средства связи с подвижными объектами». Он мо-
жет быть использован при изучении цифровой обработки сиг-
налов студентами и магистрантами близких специальностей.
УДК 621.372.083.92 (076.1)
© Васюков В.Н., Голещихин Д.В., 2004
© Новосибирский государственный
Оглавление
ВВЕДЕНИЕ 4
1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ЦОС 5
2.![]() -ПРЕОБРАЗОВАНИЕ 10
-ПРЕОБРАЗОВАНИЕ 10
3. СТРУКТУРНЫЕ СХЕМЫ И РАЗНОСТНЫЕ УРАВНЕНИЯ
ЛИС-ЦЕПЕЙ 15
4. СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ЛИС-ЦЕПИ 21
5. МНОГОМЕРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
И ЛИС-ЦЕПИ 24
6. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ 26
7. ВЗАИМОСВЯЗЬ АНАЛОГОВЫХ, ДИСКРЕТНЫХ
И ЦИФРОВЫХ СИГНАЛОВ 27
8. РЕАЛИЗАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ 28
9. СИГНАЛЬНЫЕ ПРОЦЕССОРЫ И ИХ ПРИМЕНЕНИЕ 29
10. РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ 30
СПРАВОЧНЫЙ МАТЕРИАЛ 33
ЛИТЕРАТУРА 39
Введение
Предлагаемый задачник предназначен для студентов, изучающих дисциплины «Основы цифровой обработки сигналов», «Применение цифровой обработки сигналов», «Цифровая обработка сигналов и сигнальные процессоры в системах подвижной радиосвязи». Материал задачника может быть использован преподавателями при проведении практических занятий, а также студентами для самостоятельной работы. Кроме того, представлены два расчетно-графических задания для самостоятельного выполнения студентами при изучении указанных дисциплин.
Большинство предлагаемых задач, а также расчетно-гра-фические задания составлены авторами. Некоторые задачи заимствованы из литературы по цифровой обработке сигналов [1 – 8]. Задачи распределены по разделам, в основном соответствующим разделам учебника [1].
1. Математические основы цос
Пусть
 – множество действительных чисел.
Проверьте, образует ли множество
– множество действительных чисел.
Проверьте, образует ли множество группу относительно операции сложения;
относительно операции умножения.
группу относительно операции сложения;
относительно операции умножения.Пусть
 – множество действительных чисел в
интервале [0, 1]. Образует ли множество
– множество действительных чисел в
интервале [0, 1]. Образует ли множество группу относительно операции сложения?
относительно операции умножения?
группу относительно операции сложения?
относительно операции умножения?Пусть
 – множество действительных чисел,
принадлежащих интервалу [0, 1). Проверьте,
образует ли множество
– множество действительных чисел,
принадлежащих интервалу [0, 1). Проверьте,
образует ли множество группу относительно операции сложения
по модулю 1. Операция сложения по модулю
группу относительно операции сложения
по модулю 1. Операция сложения по модулю определяется выражением
определяется выражением
![]()
Пусть
 – множество всех четных целых чисел.
Образует ли множество
– множество всех четных целых чисел.
Образует ли множество группу относительно операции сложения?
относительно операции умножения?
группу относительно операции сложения?
относительно операции умножения?Проверьте, выполняются ли аксиомы группы по сложению для:
а)
множества всех матриц; б) множества всех
матриц размера
![]() ;
в) множества всех квадратных матриц; г)
множества всех матриц размера
;
в) множества всех квадратных матриц; г)
множества всех матриц размера![]() (здесь и далее
(здесь и далее![]() и
и![]() –
различные целые положительные числа).
–
различные целые положительные числа).
Дано множество всех матриц размера
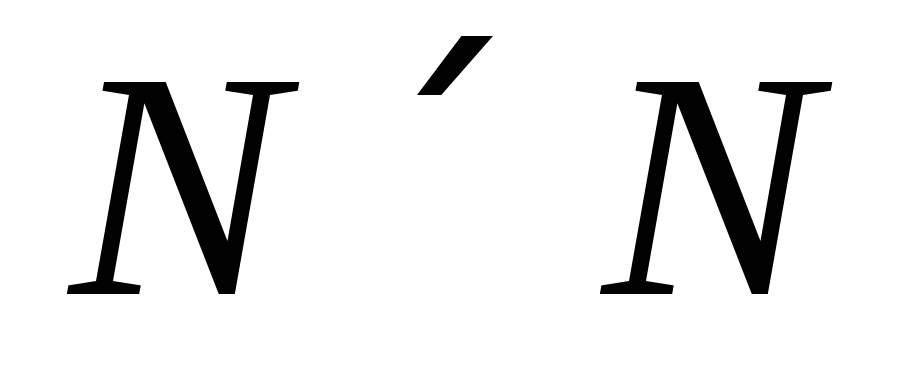 .
Проверьте, является ли это множество
группой относительно операции матричного
умножения. Если нет, то как нужно сузить
это множество, чтобы выполнялись
аксиомы группы? Что в этом случае
представляет собой нейтральный элемент?
.
Проверьте, является ли это множество
группой относительно операции матричного
умножения. Если нет, то как нужно сузить
это множество, чтобы выполнялись
аксиомы группы? Что в этом случае
представляет собой нейтральный элемент?Дано множество {0, 1}, состоящее из целых чисел 0 и 1, с операцией сложения по модулю 2 . Проверьте, является ли это множество группой. Если да, то определите нейтральный элемент. Как найти элемент, обратный данному?
Дано множество целых чисел {0, 1, 2, 3, 4} с операцией сложения по модулю 5. Проверьте, является ли это множество группой. Что представляет собой нейтральный элемент? Как найти элемент, обратный данному?
Дано множество целых чисел {0, 1}. Проверьте, составляет ли оно группу относительно «обычной» операции умножения.
Дано множество целых чисел {0, 1} с операциями сложения по модулю 2 и обычного умножения. Является ли это множество полем?
Дано множество целых чисел {0, 1, 2}. Дайте определение операций (сложения и умножения), для которых это множество образует поле. Составьте таблицы сложения и умножения.
Дано множество MN последовательностей длины N, каждая из которых определяется выражением
![]() ,
,
где
![]() ,
,![]() ;
;![]() – поле действительных чисел. Определены
операции поэлементного сложения
последовательностей и умножения
последовательности на действительное
число:
– поле действительных чисел. Определены
операции поэлементного сложения
последовательностей и умножения
последовательности на действительное
число:
![]() ,
,
![]() ,
,
![]() .
.
Проверьте
выполнение аксиом линейного пространства
для множества
MN.
Существует
ли в MN
нулевой
элемент?
Запишите
его.
Найдите
элемент, обратный последовательности
![]() .
.
Дано множество MN последовательностей длины N, каждая из которых определяется выражением
![]() ,
,
где
![]() – всевозможные комплексные числа,
вещественные и мнимые части которых не
превосходят по абсолютной величине
единицы, т.е.
– всевозможные комплексные числа,
вещественные и мнимые части которых не
превосходят по абсолютной величине
единицы, т.е.![]() ,
,![]() .
Дано поле комплексных чисел
.
Дано поле комплексных чисел![]() .
Определены операции поэлементного
сложения последовательностей и умножения
последовательности на комплексное
число. Проверьте выполнение аксиом
линейного пространства для множестваMN.
.
Определены операции поэлементного
сложения последовательностей и умножения
последовательности на комплексное
число. Проверьте выполнение аксиом
линейного пространства для множестваMN.
Дано множество М последовательностей бесконечной длины, каждая из которых определяется выражением
![]() ,
,
где![]() ,
,![]() .
Определены операции поэлементного
сложения последовательностей и умножения
последовательности на вещественное
число. Проверьте выполнение аксиом
линейного пространства для множестваM.
.
Определены операции поэлементного
сложения последовательностей и умножения
последовательности на вещественное
число. Проверьте выполнение аксиом
линейного пространства для множестваM.
Дано множество MN всех вещественных последовательностей конечной длины N, определенных при
 (см. задачу 1.12). Какова размерность
пространстваMN
? Задайте
базис для MN.
(см. задачу 1.12). Какова размерность
пространстваMN
? Задайте
базис для MN.Один из возможных базисов для пространства последовательностей
 состоит из сдвинутых
состоит из сдвинутых -последова-тельностей
-последова-тельностей .
Докажите, что набор из любого количества
таких последовательностей линейно
независим.
.
Докажите, что набор из любого количества
таких последовательностей линейно
независим.Дано множество последовательностей конечной длины
 .
Проверьте, можно ли считать метриками
следующие функции:
.
Проверьте, можно ли считать метриками
следующие функции:
а)
![]() ,
,
б)
 ,
,
в)
![]()
Пусть (M, d) – метрическое пространство, т.е. множество элементов M с определенной на нем метрикой
 .
Покажите, что функционалом
.
Покажите, что функционалом
![]()
также
можно задать метрику на M,
определив таким образом другое метрическое
пространство
![]() .
.
Пусть M – нормированное линейное пространство, норма элемента
 обозначается
обозначается .
Покажите, что функционалом
.
Покажите, что функционалом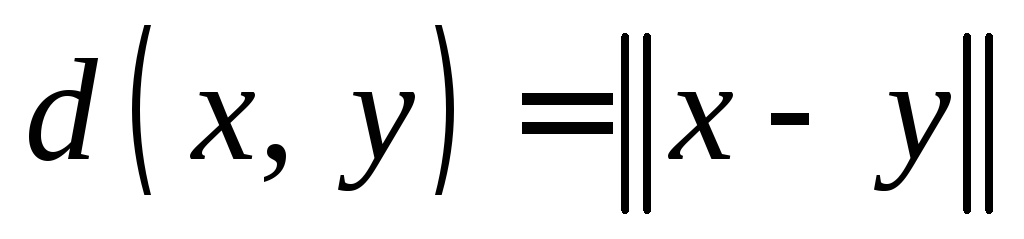 наM
задается
метрика.
наM
задается
метрика.Пусть M – линейное пространство со скалярным произведением. Покажите, что функционалом
 наM
задается
норма.
наM
задается
норма.Даны две последовательности, принадлежащие пространству M:
![]() ,
,
![]() .
.
Найдите:
нормы
![]() ,
,![]() ;
скалярное произведение
;
скалярное произведение![]() ;
угол между
;
угол между![]() и
и![]() ;
расстояние
;
расстояние![]() .
.
Даны последовательности конечной длины:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Найдите:
а) скалярное произведение
![]() ;
б) скалярное произведение укороченных
последовательностей при
;
б) скалярное произведение укороченных
последовательностей при![]() .
.
Пусть
 и
и – векторы единичной нормы в действительном
пространстве со скалярным произведением.
Покажите, что векторы
– векторы единичной нормы в действительном
пространстве со скалярным произведением.
Покажите, что векторы и
и взаимно ортогональны.
взаимно ортогональны.Найдите нормы
 последовательностей
последовательностей
а)
![]() ,
,![]() ,
,
б)
![]() ,
,![]() ,
,
в)
![]() ,
,
г)
![]() ,
,
д)
![]() ,
,
е)
![]() .
.
Проверьте, является ли линейным пространством множество всех векторов единичной нормы на плоскости с обычным сложением векторов и умножением вектора на действительный скаляр.
Покажите, что при различной нумерации исходной системы векторов
 процедура Грама–Шмидта приводит к
различным базисам.
процедура Грама–Шмидта приводит к
различным базисам.Даны последовательности
![]() ;
;
![]() ;
;
![]() ,
,
принадлежащие
пространству
![]() ,
натянутому на множество последовательностей
,
натянутому на множество последовательностей![]() .
Проверьте линейную независимость
последовательностей. Постройте
ортонормальный базис в
.
Проверьте линейную независимость
последовательностей. Постройте
ортонормальный базис в![]() .
.
Докажите, что роль единицы для алгебры
 со сверткой в качестве обобщенного
умножения играет
со сверткой в качестве обобщенного
умножения играет -последовательность
-последовательность .
.
Докажите справедливость выражения
![]() .
.
Докажите, что последовательность, принадлежащая
 ,
принадлежит также и
,
принадлежит также и .
.Докажите, что
 -норма
в трехмерном пространстве совпадает
с обычным геометрическим определением
длины (модуля) вектора.
-норма
в трехмерном пространстве совпадает
с обычным геометрическим определением
длины (модуля) вектора.
