
МММ_Лаб_#1 / Diffusion_Ch7
.pdf
Diffusion - Chapter 7
DIFFUSION - Chapter 7
Basic Concepts
VG
Silicide Sidewall
Spacers
VS |
Rpoly |
VD |
xW
Rcontact
Rsource Rext Rchan
xJ
•Placement of doped regions (main source/drain, S/D extensions, threshold adjust) determine many short-channel characteristics of a MOS device.
•Resistance impacts drive current.
•As device shrinks by a factor K, junction depths should also scale by K to maintain same ε-field
patterns (assuming the voltage supply also scales down by the same factor).
• Gate doping affects poly-depletion and limits how the gate voltage controls the channel potential.
a) |
b) |
xj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = ρ |
|
|
|
|
|
ρS = ρ/xj |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
SILICON VLSI TECHNOLOGY |
1 |
© 2000 |
by Prentice Hall |
||||||||||||
Fundamentals, |
Practice |
and Modeling |
|
|
|
Upper |
Saddle River, NJ. |
||||||||
By Plummer, |
Deal and |
Griffin |
|
|
|
|
|
|
|
|
|
||||

Diffusion - Chapter 7
• The resistivity of a cube is given by |
|||||
J = nqv = nqmε = |
1 |
|
ε |
\ r = ε Wcm (1) |
|
r |
|||||
|
|
J |
|||
• The sheet resistance of a shallow junction is
|
|
R = |
|
r |
W / Square º r |
(2) |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
x j |
|
||
• For a non-uniformly doped layer, |
|
|||||||
rs = |
r |
= |
|
|
1 |
(3) |
||
x j |
|
x j |
|
|
||||
|
|
q |
ò[n(x) - NB ] m[n(x)] dx |
|
||||
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
•Eqn. (3) has been numerically integrated by Irvin for simple analytical profiles (example later).
•Sheet resistance can be experimentally measured by a four point probe technique.
|
Year of 1st DRAM |
1 9 9 7 |
1 9 9 9 |
2 0 0 3 |
2 0 0 6 |
2 0 0 |
9 |
2 0 1 2 |
|
||||||
|
Shipment |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Min Feature Size (nm) |
2 5 0 |
1 8 0 |
1 3 0 |
1 0 0 |
7 0 |
|
5 0 |
|
||||||
|
DRAM Bits/Chip |
256M |
1 G |
4 G |
1 6 G |
6 4 G |
2 5 6 G |
|
|||||||
|
Minimum |
Supply |
1 . 8 - |
1 . 5 - |
1 . 2 - |
0 . 9 - |
0 . 6 |
- |
0 . 5 - 0 . 6 |
|
|||||
|
Voltage |
(volts) |
2 . 5 |
1 |
. 8 |
1 |
. 5 |
1 |
. 2 |
0 . 9 |
|
|
|||
|
Gate Oxide Tox |
4 - 5 |
3 |
- 4 |
2 |
- 3 |
1 . 5 - 2 |
< 1 . |
5 |
< 1 . 0 |
|
||||
|
Equivalent (nm) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Sidewall |
Spacer |
1 0 0 - |
7 |
2 - |
5 |
2 - |
2 0 |
- 4 0 |
7 . 5 |
- |
5 - 1 0 |
|
||
|
Thickness |
xW (nm) |
2 0 0 |
1 4 4 |
1 0 4 |
|
|
1 5 |
|
|
|
||||
|
Contact xj (nm) |
1 0 0 - |
7 |
0 - |
5 |
0 - |
4 0 |
- 8 0 |
1 5 - 3 0 |
1 0 - 2 0 |
|
||||
|
|
|
|
|
2 0 0 |
1 4 0 |
1 0 0 |
|
|
|
|
|
|
||
|
xj at Channel (nm) |
5 0 - |
3 6 |
- 7 2 |
2 6 |
- 5 2 |
2 0 |
- 4 0 |
1 5 - 3 0 |
1 0 - 2 0 |
|
||||
|
|
|
|
|
1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
Drain Ext Conc (cm-3) |
1x101 8 |
1x101 9 |
1x101 9 |
1x102 0 |
1x102 0 |
1x102 0 |
|
|||||||
SILICON VLSI TECHNOLOGY |
2 |
|
|
|
|
© 2000 by Prentice Hall |
|||||||||
Fundamentals, |
Practice |
and Modeling |
|
|
|
|
|
|
Upper |
Saddle River, NJ. |
|||||
By Plummer, |
Deal and |
Griffin |
|
|
|
|
|
|
|
|
|
|
|
||

Diffusion - Chapter 7
•Diffusion is the redistribution of atoms from regions of high concentration of mobile species to regions of low concentration. It occurs at all temperatures, but the diffusivity has an exponential dependence on T.
•Predeposition: doping often proceeds by an initial predep step to introduce the required dose of dopant into the substrate.
•Drive-In: a subsequent drive-in anneal then redistributes the dopant giving the required junction depth and surface concentration.
"Predep" |
|
Drive-in |
|
controlled dose |
|
||
Silicon |
constant dose |
||
|
|||
|
|
|
|
Ion Implantation and |
Solid/Gas Phase Diffusion |
|
||
|
|
|
Annealing |
|
|
|
Advantages |
|
Room temperature mask |
No damage created by doping |
|
||
|
|
Precise dose control |
|
Batch fabrication |
|
|
|
|
1011 - 1016 atoms cm-2 doses |
|
|
||
|
|
Accurate depth control |
|
|
||
Problems |
|
|
|
|
||
|
Implant damage enhances |
Usually limited to solid |
||||
|
|
diffusion |
|
solubility |
|
|
|
|
Dislocations caused |
by |
Low surface concentration |
|
|
|
|
damage may cause junction |
hard to achieve without a |
|
||
|
|
leakage |
|
long drive-in |
|
|
|
|
Implant channeling may |
Low dose predeps very |
|
||
|
|
affect |
profile |
|
difficult |
|
SILICON VLSI TECHNOLOGY |
3 |
© 2000 by Prentice Hall |
||||
Fundamentals, |
Practice |
and Modeling |
|
Upper Saddle River, NJ. |
||
By Plummer, |
Deal and |
Griffin |
|
|
|
|

Diffusion - Chapter 7
• Dopants are soluble in maximum value before another phase.
bulk silicon up to a they precipitate into
|
1022 |
|
|
|
|
|
) |
|
|
|
|
As |
|
3 |
|
|
|
|
|
|
- |
|
|
P |
|
|
|
cm |
|
|
|
|
|
|
1021 |
|
|
|
|
|
|
(atoms |
|
|
|
|
|
|
|
|
|
B |
|
|
|
Solubility |
1020 |
|
Sb |
|
|
|
Sn |
|
|
|
|
||
|
|
|
|
|
||
Solid |
|
Ga |
|
|
|
|
|
Al |
|
|
|
|
|
|
1019 |
|
|
|
|
|
|
|
|
|
1200 |
1300 |
|
|
800 |
900 |
1000 |
1100 |
Temperature (˚C)
• Dopants may have an “electrical” solubility that is different than the solid solubility defined above.
Si |
As |
As+ |
V |
• As4V is one possible electrically inactive form.
SILICON VLSI TECHNOLOGY |
4 |
© 2000 |
by Prentice Hall |
||
Fundamentals, |
Practice |
and Modeling |
|
Upper |
Saddle River, NJ. |
By Plummer, |
Deal and |
Griffin |
|
|
|

Diffusion - Chapter 7
• Macroscopic dopant redistribution is described by Fick’s first law, which describes how the flux (or flow) of dopant depends on the doping gradient.
Concentration
F = −D |
∂C |
(4) |
|
∂x |
|
 F = - D dC/dx
F = - D dC/dx
t1 t2
Distance
•This is similar to other laws where cause is proportional to effect (Fourier’s law of heat flow, Ohm’s law for current flow).
•Proportionality constant is the diffusivity D in cm2 sec-1. D is related to atomic hops over an energy barrier (formation and migration of mobile species) and is exponentially activated. D is isotropic in the silicon lattice.
•Negative sign indicates that the flow is down the concentration gradient.
SILICON VLSI TECHNOLOGY |
5 |
© 2000 |
by Prentice Hall |
||
Fundamentals, |
Practice |
and Modeling |
|
Upper |
Saddle River, NJ. |
By Plummer, |
Deal and |
Griffin |
|
|
|

Diffusion - Chapter 7
• Fick’s second law describes how the change in concentration in a volume element is determined by the change in fluxes in and out of the volume.
Fin Fout
C
|
|
x |
|
|
|
|
|
|
|
• Mathematically |
|
|
|
|
|
|
|
|
|
¶C |
= |
¶F |
= |
¶ æ |
D |
¶Cö |
(5) |
||
|
|
|
|
|
|||||
¶t |
¶x |
¶x è |
¶x ø |
||||||
|
|
|
|
||||||
• If D is a constant this gives
¶C |
= D |
¶2C |
(6) |
||
¶t |
¶ |
2 |
|||
|
|
||||
|
x |
|
|||
•This is the only form of Fick's second law which can be solved analytically. We will consider a number of closed form solutions.
•Modern silicon processing rarely satisfies the restrictive conditions for these solutions to apply (e.g. D = constant), so these solutions are only rough guidelines to real profiles.
SILICON VLSI TECHNOLOGY |
6 |
© 2000 |
by Prentice Hall |
||
Fundamentals, |
Practice |
and Modeling |
|
Upper |
Saddle River, NJ. |
By Plummer, |
Deal and |
Griffin |
|
|
|

Diffusion - Chapter 7
Solutions Of Fick’s Laws
1. Limited Source: Consider a fixed dose Q, introduced as a delta function at the origin.
Dose Q
Diffused Gaussian

 x 0
x 0
• The solution that satisfies Fick’s second law is
C(x, t) = |
|
Q |
æ |
- |
x2 ö |
|
|
|
|
expç |
|
÷ |
(7) |
||
|
pDt |
|
|||||
2 |
è |
|
4Dtø |
|
|||
•Important consequences:
1.Dose Q remains constant
2.Peak concentration decreases as 1 / t
3.Diffusion distance from origin increases as
|
|
|
2 |
Dt |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
t=t |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0.8 |
|
t=4*t |
0 |
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t=9*t |
0 |
|
|
|
|
|
|
|
Concentration |
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
0.01 |
|
0.4 |
|
|
|
|
|
|
|
|
|
0.001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
0.0001 |
|
0 |
|
|
|
|
|
|
|
|
|
10 - 5 |
|
-5 |
-4 |
-3 -2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
X (Units of Diffusion Distance 2√Dt0) |
|
|
||||||
|
|
|
t=t |
|
|
|
|
|
0 |
|
|
|
|
|
t=4*t |
0 |
|
|
|
|
|
|
|
|
|
|
t=9*t |
0 |
|
|
|
|
|
|
|
-5 |
-3 |
-1 |
1 |
3 |
5 |
|
X (Units of Diffusion Distance 2√Dt0) |
|
|||
SILICON VLSI TECHNOLOGY |
7 |
© 2000 |
by Prentice Hall |
||
Fundamentals, |
Practice |
and Modeling |
|
Upper |
Saddle River, NJ. |
By Plummer, |
Deal and |
Griffin |
|
|
|

|
|
|
|
Diffusion - Chapter 7 |
2. Constant Source Near A Surface: |
||||
Imaginary |
|
|
|
Delta Function |
Delta Function |
|
|
|
Dose Q |
|
|
|
||
Dose Q |
|
|
|
(Initial Profile) |
Virtual |
|
|
|
Diffused |
Diffusion |
|
|
|
Gaussian |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
Q |
æ |
|
x2 ö |
æ |
|
|
x2 ö |
||
C(x, t) = |
|
|
expç |
- |
|
÷ |
= C(0, t)expç |
- |
|
÷ (8) |
|
|
pDt |
|
|
||||||||
|
|
è |
|
4Dtø |
è |
|
|
4Dtø |
|||
3. Infinite Source: The infinite source is made up of small slices each diffusing as a Gaussian.
Dose C x
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Initial |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Profile |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Diffused |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Profile |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
(x - xi ) |
2 |
|
|
||||||
|
|
|
C(x, t) = |
|
|
|
|
C |
|
|
n |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
å Dxi exp- |
4Dt |
|
|
(9) |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
pDt i=1 |
|
|
|
|
|
|
|
||||||||||
• The solution which satisfies Fick’s second law is |
||||||||||||||||||||||||||
C(x, t) = |
C' |
é1 - erfæ |
|
|
x |
ö ù |
= C |
éerfcæ |
x |
|
ö ù |
(10) |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
ê |
|
|
è |
|
|
ú |
|
|
S ê |
|
è 2 Dt |
ú |
|
||||||||||||
|
2 ë |
|
|
2 Dt ø û |
|
|
ë |
|
ø û |
|
||||||||||||||||
SILICON VLSI TECHNOLOGY |
|
|
8 |
|
|
|
|
|
© 2000 by Prentice Hall |
|||||||||||||||||
Fundamentals, |
Practice and Modeling |
|
|
|
|
|
|
|
|
|
Upper |
Saddle River, NJ. |
||||||||||||||
By Plummer, |
Deal and Griffin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

Diffusion - Chapter 7
Important consequences of error function solution:
•Symmetry about mid-point allows solution for constant surface concentration to be derived.
•Error function solution is made up of a sum of Gaussian delta function solutions.
•Dose beyond x = 0 continues to increase with annealing time.
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t=9*t |
|
|
|
0.8 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
t=4*t |
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Initial |
|
|
|
0.6 |
|
|
|
|
|
|
|
t=t |
0 |
|
√Dt) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
erf(x/2 |
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
-5 |
-4 |
-3 |
-2 -1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
X (Units of 2√Dt |
0 |
) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(See Appendix A.9 in text for properties of erfc.)
4. Constant Surface Concentration: (just the right hand side of the above figure).
|
|
|
|
C(x, t) = C |
éerfc |
|
|
x |
ù |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
S ê |
|
2 |
ú |
||||||
|
|
|
|
|
|
|
|
ë |
|
|
Dt û |
|||||
• Note that the dose is given by |
|
|
|
|||||||||||||
Q = |
∞ |
é1 - erfæ |
|
x |
|
ö |
ù |
= |
2CS |
|
|
|||||
ò |
C |
|
|
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
S ê |
è 2 |
Dt ø |
ú |
|
|
|
p |
|||||||
|
0 |
|
ë |
û |
|
|
|
|||||||||
SILICON VLSI TECHNOLOGY |
|
9 |
|
|
|
|
|
|
|
|
||||||
Fundamentals, Practice |
and |
Modeling |
|
|
|
|
|
|
|
|
|
|
||||
By Plummer, Deal |
and Griffin |
|
|
|
|
|
|
|
|
|
|
|||||
(11)
Dt (12)
© 2000 by Prentice Hall Upper Saddle River, NJ.
Diffusion - Chapter 7
Intrinsic Dopant Diffusion Coefficients
• Intrinsic dopant diffusion coefficients are found to be of the form:
|
|
|
D = D |
0 |
æ |
-EA ö |
|
(13) |
|
|
|
|
exp |
è |
kT ø |
|
|||
|
|
|
|
|
|
|
|
||
|
S i |
B |
In |
|
A s |
|
Sb |
P |
Units |
D0 |
560 |
1 . 0 |
1 . 2 |
|
9 . 1 7 |
|
4 . 5 8 |
4 . 7 0 |
cm2 sec-1 |
EA |
4 . 7 6 |
3 . 5 |
3 . 5 |
|
3 . 9 9 |
3 . 8 8 |
3 . 6 8 |
e V |
|
• Note that ni is very large at process temperatures, so "intrinsic" actually applies under many conditions.
|
|
|
|
T |
(˚C) |
|
|
|
|
1200 |
1100 |
1000 |
9 0 0 |
|
8 0 0 |
|
|
|
1 0- 1 1 |
|
|
|
|
|
|
|
- 1 ) |
1 0- 1 3 |
|
|
|
|
|
|
|
sec |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
(cm |
1 0- 1 5 |
|
|
|
|
In |
|
|
Diffusivity |
|
|
|
|
|
|
||
|
|
|
|
P |
|
B |
|
|
|
|
|
|
|
|
|
||
1 0- 1 7 |
|
|
|
|
|
Sb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A s |
|
|
|
1 0- 1 9 |
|
|
|
|
|
|
|
|
0 . 6 5 |
0 . 7 |
0 . 7 5 0 . 8 0 . 8 5 |
0 . 9 |
0 . 9 5 |
1 |
||
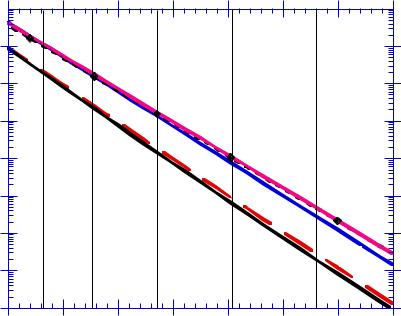
|
|
|
|
1000/T |
(Kelvin) |
|
|
|
• Note the "slow" and "fast" diffusers. Solubility is also an issue in choosing a particular dopant.
SILICON VLSI TECHNOLOGY |
1 0 |
© 2000 |
by Prentice Hall |
||
Fundamentals, |
Practice |
and Modeling |
|
Upper |
Saddle River, NJ. |
By Plummer, |
Deal and |
Griffin |
|
|
|
