1. Вывод обыкновенного уравнения диффузии:

Диффузией называют перенос вещества в направлении убывания их концентрации, обусловленный тепловым движением атомов.

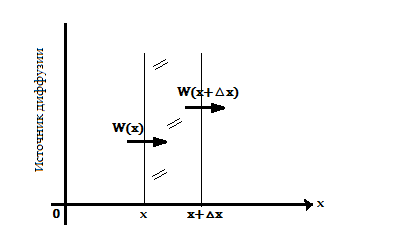
Рисунок 1

Рассмотрим полупроводниковую пластину бесконечной длины. Выделим определенную область (x; x+△x) и рассмотрим в определенный момент времени (t;t+△t). Для того чтобы рассчитать скорость изменения концентрации, нужно взять интеграл по всему объему, он равен разности потоков через боковые стенки.

при △x→0 получаем однородное уравнение диффузии

(1.1)

W – поток внедряемой примеси внутри вещества, определяется суммой диффузионного и дрейфового потоков.

,

где – это коэффициент подвижности

D= , где – тепловой потенциал (соотношение Эйнштейна)

z=

Выражение для полного потока будет иметь вид:

Подставляем это выражение в II закон Фика и получаем уравнение диффузии

б)в случае трехмерного приближения

Выделим элемент dS.

Чтобы определить поток примеси, плотностью W, протекающий через элементарный объем, нужно взять двойной интеграл.

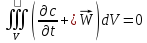
Устремим этот элементарный объем к 0

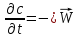
=-Dc

2. Запись диффузионной модели в виде ящика

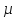D z

T

Модель C(x)

t

Внешняя среда

Рисунок 2. Диффузионная модель в виде ящика

Входные параметры:

– коэффициент диффузии

µ - подвижность,

– постоянная Больцмана,

– элементарный заряд,

T – температура,

t – время.

Выходные параметры:

С(х) – распределение дифундирующего вещества

3. Построение в EXCEL графиков Аррениуса для коэффициентов диффузии бора, фосфора, мышьяка и сурьмы в кремниевой пластине и определение коэффициента диффузии этих примесей по графику для Т=1000°С

T(0C)	D(B) cm2sec-1	D(P) cm2sec-1	D(As) cm2sec-1	D(Sb) cm2sec-1
1000	1,26897E-14	1,27E-14	1,46E-15	1,993E-15

1.4 Анализ диффузионной модели:

а) Проверка идентичности размерностей различных слагаемых в уравнении диффузии;

б) Анализ математического типа уравнения в диффузионной модели;

Типы уравнений: эллиптические, гиперболические, параболические.

- уравнение в частных производных

С=С(x,t). D=const

U=U(x,y)

Дискриминант = B²-4AC

Если Д=0 – параболический тип уравнения

Д>0 – гиперболический

Д<0 – эллиптический

А=D

B=0

C=0

B²-4AC=0-0=0 => параболическое уравнение.

в) Описание краевых задач, имеющих аналитическое решение:

— Для точечного диффузионного источника (модель диффузии с постоянной дозой); качественный вид решения для трех временных моментов;

Уравнение диффузии (первый закон Фика):

Область моделирования:

Начальные условия:

t=0

Граничные условия:

x=0

условие отражения на левой границе

на правой границе:

x→∞

C(∞;t)=0

Количество внедренной примеси Q(t) – доза- за время загонки t задается интегралом:

Решением этой краевой задачи является уравнение Гаусса:

— Для диффузионной загонке примеси с постоянной поверхностной концентрацией; качественный вид решения для трех временных моментов;

Уравнение диффузии (первый закон Фика):

Область моделирования:

Граничные условия:

при x→0

при x→∞

Начальные условия:

t=0

Решением этой краевой задачи будет дополняющая функция ошибок erfc(x)

-График спец. функций erf(z) и erfc(z) с описанием их математических свойств.

В математике функция ошибок (функция Лапласа) — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как

.

Дополнительная функция ошибок, обозначаемая  определяется через функцию ошибок:

.

НО! В нашем случае концентрации по смыслу не могут зависеть от отрицательного аргумента, значит, графики будут выглядеть так:

Свойства:

• Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:

для

при

-Расчет дозы легирования и поверхностной концентрации для случаев:

а) распределения примеси по Гауссу;

б) распределения примеси по erfc(z);

а) Для случая распределения примеси по Гауссу

Распределение примеси по Гауссу имеет вид:

Найдем внедренную дозу , проинтегрировав концентрацию примеси по всей области моделирования:

Этот интеграл является табличным Гауссовым интегралом

Значит,

Внедренная доза является константой.

Поверхностная концентрация находится из условия:

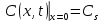
Отсюда видно, что поверхностная концентрация примеси уменьшается со временем, что и характерно для диффузии примеси из точечного источника.

б) Для распределения по

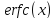
Распределение примеси по erfc имеет вид:

Вся доза поступает непосредственно через границу вещества в точке , её можно найти проинтегрировав по всему промежутку времени поток внедряемой примеси через эту границу.

Найдем выражение для потока:

Подставим поток и проинтегрируем:

При бесконечном источнике, внедренная доза является функцией времени.

г)Задача с неоднородными начальными условиями

Под неоднородными условия подразумевается то, что изначально пластина не является чистой.

Начальные условия:

С^’ (x,0)=0

Граничные условия:

С^’(0,t)=C_s – C₀ ( пластина легирована на поверхности)

С^’=(C_s – C₀)*erfc

Частный случай: Cs = 0 (пластина легирована однородно), в таком случае задача сводиться к задаче с однородными условиями.

Примись отходит от границы