Некоторые вычислительные особенности слау

Погрешности и невязки

Для оценки точности найденного решения СЛАУ существует две общеупотребительной меры погрешности:

1. вектор ошибок

где точное решение

-найденное решение

Мера абсолютно точная, только для того, чтобы ею пользоваться нужно

Чтобы избежать трудностей, вводят другую меру

2. вектор невязок

Невязка - количественная мера несоответствия между правыми и левыми частями системы уравнений при подстановки в них вычислительного решения.

Очевидно, что равенство нулю вектора ошибок влечет за собой равенство нулю вектора невязок.

Однако, в общем случае из малости величины невязок не следует малость ошибки. Т.е. несмотря на то, что найденное решение почти удовлетворяет уравнению, оно может совсем не подходить в качестве подлинного решения. Невязка полезна в том смысле, что с ее помощью можно осуществить контроль точности решения. Т.к. использовать в качестве меры контроля вектор ошибок не представляется возможным в виду того, что неизвестно точное решение.

Пример. Рассмотрим систему

Предположим, что мы провели вычисления (неважно каким методом) и нашли решение

Если вычислить невязки, то невязки будут равны

Для погрешность 10^-2, но точное решение

В общем случае можно утверждать, что для оценки величины невязки и погрешности можно использовать следующие формулы:

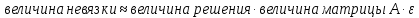
Число называется числом обусловленности матрицы А и математически оно показывает, насколько матрица системы А близка к вырожденной или иными словами, числомера вырождения матрицы А, а именно, чем выше, тем ближе матрица к вырождению.

Обусловленность- это внутреннее свойство матрицы СЛАУ. Оно не связано с каким либо численным методом. В общем случае, можно утверждать, что матрица с большим числом обусловленности дает большие ошибки при решении СЛАУ.

Математически точно число обусловленности можно вычислить.

Введем число ;

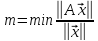
Тогда число обусловленности представляет собой:

Тогда мы можем утверждать, что погрешность решения:

Вычислительная эффективность правила Крамера

Правило Крамера широко применяется для нахождения решения СЛУ

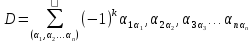
Если сосчитать количество операций, которых нам надо сделать

n	3	10	20
N	17	3.6*107	5*1019
t

Численные методы решения СЛАУ

Все численные методы решения СЛАУ принято делить на два класса:

1. прямые

2. итерационные

Прямые методы используют некоторые формулы для вычисления неизвестных величин за конечное число шагов вычислительного процесса

Пример. Метод обратной матрицы

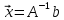
Существенным недостатком прямых методов является необходимость хранения в памяти компьютера всех n- квадратных элементов матрицы системы, т.е прямые методы никаким образом не учитывают разряженную структуру матрицы в системы.

Кроме этого применения прямых методов для решения СЛАУ с большим числом переменных приводит к значительному накоплению вычислительных погрешностей.

К широко известным методам относится метод Гаусса, метод прогонки.

Итерационные методы ( методы последовательных приближений)-это методы, в которых с помощью какого- либо алгоритма строится цепочка приближенных решений

Каждый цикл таких вычислений называется итерацией.

Итерационные алгоритмы сложнее прямых методов. Объем необходимых вычислений при их использовании заранее трудно определить, но они не требуеют при работе с разряженными матрицами хранение всех ее элементов. Более того, зачастую в них используются вычислительные формулы, задающие эти примеры. Итерационный процесс устроен таким образом, что вычислительные ошибки от итерации к итерации не накапливаются. Поэтому итерационный метод можно использовать как для решения хорошо обусловленных так и плохообусловленных СЛАУ.

Примеры: Метод простой итерации и метод Гаусса- Зейделя

Метод исключения Гаусса

Хорошо известно, что алгоритм метода Гаусса для решения СЛАУ состоит из двух основных шагов.

1. На прямом ходе путем последовательного исключения переменных из уравнений системы, матрицу системы приводят к треугольному виду.

решение методом исключения дает верхнетреугольную матрицу:

2. На обратном ходе вычисляется точное решение системы

подставляем в предыдущее уравнение и получаем:

Метод Гаусса применим эффективно лишь в том случае, когда матрица системы хорошо обусловлена, имеет низкое число обусловленности.

Точность вычисления значительно зависит от способа нахождения ведущего элемента, который мы используем, для исключения переменных на прямом ходе.

Пример.Рассмотрим систему:

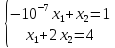
Возьмем в качестве ведущего элемента

При решении получим:

если округлить, то примерно получим, что неправильно!

Теперь, возьмем в качестве ведущего элемента коэффициент перед из второго уравнения, т.е 1.

Тогда, если округлить, то получим правильное решение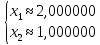

Правила для выбора ведущего элемента:

1. выбор по столбцам

Рассматривается первый столбец. Предполагается, что мы хотим исключить 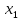. Находим в этом столбце максимальный элемент, т.е. Находим уравнение, где коэффициент присамый большой и переставляем это уравнение на первое место и используем коэффициент прив качестве ведущего элемента.

2. выбор по строке

Из первого уравнения находим переменную, которую будем исключать. Ищем и ищем соответственно, которое соответствует этому максимальному элементу. И ставимна первое место и исключаем его.

Эту методику можно обобщить на все элементы

3. по всей матрице

Сканируем столбцы и строчки и ищем 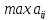. Находим, и ставим этот элемент на первое место .

Этот прием наиболее приемлем.

Метод прогонки

Метод прогонки является частным случаем метода Гаусса, который специально предназначен для решения систем уравнений с разряженной диагональной матрицей

1. Прямой ход состоит в том, что вычисляются коэффициенты

Сам процесс состоит в следующем.

2. Обратная прогонка соответствует вычислению переменных в обратном порядке, начиная с самого последнего x

зная , можно найти

Итерационные методы

В общем случае схема итерационных методов решения СЛАУ заключается в следующем:

1. каким- либо посторонним способом нужно установить, какое- либо начальное решение

2. вычисляем правую часть:

3. находим невязку:

4. находим решение системы уравнений: ,- вектор поправок

5. 

6. из 5. пункта идем во 2.

Важным вопросом является, когда нужно остановиться!

В качестве остановки используют какое- либо векторное неравенство, которое сравнивает решения, полученные на предыдущей и последующей итерации.

Введем норму: