Вычислительная машинная погрешность

Любое действительное число, обрабатываемое на компьютере, возникает с ошибкой,

b₁, b₂- целые числа

условие необходимое, чтобы это представление было единственным

При введении числа в компьютер

РС

Если , то, потому что чисел в мантиссе неограниченно

Хвост исчезает, он вводит погрешность

Те числа, которые мы вводим в компьютер можно записать множеством компьютерных действительных чисел.

Множество состоит из бесконечного числа элементов.

В процессе отбрасывания, возникают две ошибки:

1. -абсолютная погрешность

2. - относительная погрешность

Чтобы оценить первую величину:

Поскольку мы берем по модулю

Таким образом, абсолютная погрешность довольно легко оценивается, если знаем параметры.

Относительная погрешность

Таким образом, компьютерное множество действительных чисел описывается :

- порядок степени исчисления

m- количество разрядов в мантиссе

n₁,n₂-минимальное и максимальное число.

Количество чисел в мантиссе

В вычислительной математике зачастую удобно использовать:

• -основание системы исчисления

• М₀- минимальное действительное машинное число

• - машинное эпсилон; относительное ошибка определения единицы

• М_∞- максимальное машинное число

Если , то на интервале (нет никаких компьютерных чисел.

Если введем в компьютер x, то фактически мы записываем число вида:

Архитектура современных ЭВМ имеет архитектуру стандарта IEEE 754

Все компьютерные числа делятся на:

	Одинарная точность	Удвоенная точность
	2	2
n1	-125	-121
n2	128	1024
m	24	53
M0	2-126	2-1022
M∞	2128(1-2-24)	21024(1-2-53)
	2-23	2-52

Численное решение систем линейных алгебраических уравнений

В общем виде

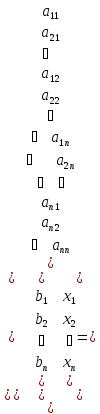
Пример 1. Интерполяция данных с помощью линейных уравнений

Рассмотрим три точки: (1;0); (2;-1); (3;2)

Предположим, что через эти три точки нужно провести параболу, т.е. определить коэффициенты уравнения

Запишем три уравнения:

Решения: a=5; b=-7; c=2.

Пример 2. Аппроксимация ( выравнивание данных) методом наименьших квадратов или эмпирическое моделирование

Предположим, что задано m точек вида, так что

Считаем, что неизвестная функцияy(t) это есть линейная комбинация каких – то базисных функций(и с добавлением шума(

,

Если мы работаем с полиномами, то базисные функции выглядят следующим образом:

Часто в качестве базисных функций выбирают тригонометрические функции и exp

Важно, чтобы входил линейно

Теперь, требование интерполяции сменяются требованиями аппроксимации.

Нарисуем такую кривую, которая должна проходить вблизи существующей.

Если в каждой экспериментальной точке задаем величину отклонения между экспериментальным числом и числом из эмпирической модели.

Составим сумму квадратов этих отклонений по всем экспериментальным точкам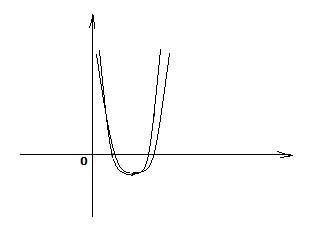

Коэффициенты выбираются таким образом, чтобы сумма квадратов была минимальна.

исптывает экстремум, когда частные производные равны 0

Если сделаем прямую подстановку, то система будет выглядеть так:

Если ввести обозначения

то система уравнений будет выглядеть так:

В методе возникает задача решение СЛУ и нахождение коэффициентов

В самом простейшем случае:

Регрессионный анализ.

Исходная модель:

Система уравнений:

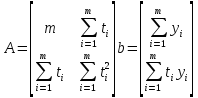
собственная система алгебраических линейных уравнений

Пример 3. Случай с разряженной матрицей или СЛАУ, которая возникает при решении двухточечной краевой задачи

Предположим, что есть дифференциальные уравнения второго порядка, рассматриваемые на интервале [0;1). Т.к. уравнения второго порядка, нам необходимо два граничных условия.

Наш интервал разобьем на равномерное число точек, h- равномерное расстояние между точками. Будем искать в точках x_iзначение функцииy_i

,n-количество точек учавствующие в интервале

Чтобы составить систему уравнений , нужно преобразовать вторую производную

Таким образом в каждой точке x_i

Подставляем полученное выражение в и получаем систему уравнений

Матрицы, у которых большая часть элементов равна нулю, называется разряженными.

Матрицы, у которых ненулевые элементы группируются возле диагонали, называется ленточными матрицами.

Решить следующую краевую задачу

Шаг сетки h=0.25

Рассмотрим краевую задачу для функции двух переменных.

Если применим к задаче рассматриваемую методику, то получим систему