
- •Анализ математической модели
- •Вычислительный эксперимент
- •Основные особенности вычислительного эксперимента в его сравнении с натуральным
- •Основные особенности компьютерных вычислений
- •Вычислительная машинная погрешность
- •Численное решение систем линейных алгебраических уравнений
- •Некоторые вычислительные особенности слау
Лекция №1 Математическое моделирование и вычислительный эксперимент
Первое понятие о математическом моделировании
Модель (от лат. modulus— «мера, аналог, образец») - копия объекта или явления, которая служит для описания и изучения объекта.
Математическая модель какого-либо объекта или явления – приближенное описание, выраженное с помощью математической символики. Под математическим моделированием понимается изучение явления или объекта, с помощью математической модели
Хорошо известно, что процесс научного познания мира основан на двух подходах:
1) эксперимент с наблюдением
2) теоретическое положение
При этом математическое моделирование не является простым расширением теории или эксперимента, а представляет собой третий способ познания мира.
Обычно моделирование используется для вычисления таких величин, которые нельзя получить из ограниченных своих возможностей. В этом случае, когда теория дает желаемые количественные результаты, математическое моделирование вряд ли необходимо.
Но моделирование часто позволяет расширить теоретические представления, с целью получения новых эмпирических понятий в тех областях, где они не могут быть получены иным способом.
В общем случае математическое моделирование подразделяется на ряд этапов:
Построение математической модели
разработка физической модели
разработка, собственно, математической модели
Этап решения прямой задачи
Этап решения обратной задачи
Этап развития математической модели
1. Построение математической модели
При построении математической модели, обеспечивается ее формулировка и постановка задачи. При этом требуется широкое знание и использование различных фактов, относящееся к изучаемому объекту или явлению, и глубокое проникновение в их взаимосвязь. Как правило, данный этап относится на стоке различных наук, и для успешной реализации необходимо совместная работа различных специалистов.
2. Этап решения прямой задачи
При решении прямых задач предполагается поведение исследования математических задач, которым приводится математическая модель, которая представляется в виде ящика (белого, черного, серого).

Ящик описывает собственно модель.
Если математическую модель и ее результат можно представить в виде математического оператора, то прямую задачу можно представить следующим образом:
А- оператор
Y=AX
3) Этап обратной задачи
Происходит разрешения данного операторного уравнения
Y,A-1, гдеA-1- обратный оператор
X=A-1Y
На данном этапе происходит согласование результатов физического эксперимента с теоретическим исследованием модели, в пределах, задаваемых с точностью наблюдения.
Здесь устанавливается взаимосвязь между математическими и физическими описаниями модели. Если такую взаимосвязь оказывается невозможно установить ни при каком выборе параметров характеристик, то модель признается непригодной для исследования рассматриваемых явлений и объектов, то есть признается неутвержденной.
Критерий истины - практика.
4) Этап развития математической модели
Производится анализ модели, в связи с новыми накопленными знаниями об изучаемых явлениях и объектах
Цель:модернизация и уточнение математической модели
Математическая запись модели может быть осуществлена в произвольном виде, например в виде таблицы или графиков.
В области микро - и наноэлектроники, чаще всего модель моделируется в виде математических уравнений: дифференциальные уравнения и уравнения с частными производными, реже интегральные , алгебраические и трансцендентные.
Полученная система математических уравнений, совместно с известными вспомогательными данными (начальные условия, значение коэффициентов уравнений, граничные условия) и образует собственно математическую модель.
При этом математическая модель должна обладать следующими характеристиками:
адекватностью, то есть, степенью соответствия физических реальных процессов и их характеристик к их модельному представлению
точностью, то есть позволяет оценивать в пределах точности наблюдения входных данных, интегральные выходные характеристики
экономичностью, то есть характеризуется временными затратами и затратами других ресурсов, необходимых для подготовки модели, ее реализации и обработки результатов
Поэтому при построении модели происходит катастрофа от изобилия, то есть приходится выбирать один конкретный тип модели при существовании других.
В процессе моделирования нужно учитывать:
В настоящий момент времени уровень точности, достигаемой с помощью математической модели, очень высок, и поэтому зачастую необходимую для практики информацию можно получить исходя из анализа модели, не прибегая ни к какому практическому исследованию реального объекта или явления
В процессе математического моделирования даже использование компьютера все решения принимает исследователь. Вся ответственность лежит на авторе.
Пример №1 Математическая модель, описывающая перенос вещества в твердом теле.
Перенос вещества в твердом теле реализуется с помощью двух механизмов:
Рассмотрим процесс перемещения примеси в пластине на некотором участке.

Рис.5. Изменение профиля легирования с течением времени.
J=Jдиф+Jдрейф
С=С(x,t)= [aтом/см3] - распределение концентрации легирующей примеси по пространственному направлению, описываемому переменной х для момента времениtили профиль легирования.
Диффузионная компонента
 (1-D)
(1-D)
В простейшем случае при малых значениях концентраций легирующей примеси коэффициент диффузии пространственно постоянен (не зависит от х) и определяется законом Аррениуса:

Т - абсолютная температура в градусах Кельвина [°K]
 [Дж/К]
- постоянная Больцмана
[Дж/К]
- постоянная Больцмана
Дрейфовая компонента
Дрейф - направление движения заряженных частиц в электрическом поле.
Под плотностью потока скалярной величины понимают количество этой величины, которое проходит через единицу площади Sза единицу времениt.

C - концентрация частиц
 -
дрейфовая скорость
-
дрейфовая скорость
(Средняя дрейфовая скорость пропорциональна напряженности поля Е: v =μE )
 -подвижность,т.е. скорость частиц в единичном полеEс напряженностью 1 В/см
-подвижность,т.е. скорость частиц в единичном полеEс напряженностью 1 В/см
z- учитывает знак:z= +1 – донорная примесь
z= -1 – акцепторная


Рассмотрим элементарную ячейку во время t и t+△t
Используем уравнение баланса массы: изменение массы вещества на отрезке x+△xравно изменению потоков через границы между временными потоками t и t+△t


△t→0; △x→0
Изменение концентрации примеси (уравнение переноса в дифференциальном виде):
 II
закон Фика (1D)
II
закон Фика (1D)
Подстановка

дает уравнение диффузии:
 (1-D)
(1-D)
В трехмерном случае, поток движется по трем координатам

Лекция №2
Модель переноса вещества в твердом теле
Задача. Показать, что в том случае если E( x ) = const, то в этом случае уравнение диффузии имеет следующий вид:

Общий случай диффузии
 уравнение непрерывности
уравнение непрерывности
где, GN - скорость генерации
RN- скорость рекомбинации
Задача 2.
Е=0

Н.У.
t=0; C(x;0)=0
Предположим, что в точке x=0 концентрация на поверхности постоянна
C(0;t)=Cs
При x→∞ концентрация легирующей примеси равна 0
x→∞ С(∞;t)=0
Г.У.
x=0 С(0;t)= Cs
x→∞ C(∞;t)=0
Решением этой краевой задачи будет дополняющая функция ошибок erfc(x)

Изменим условия процесса диффузии.
Предположим, что в пластину внедряют примесь с помощью укола (шприца)

Н.У. С(x;0)=Qδ(x)- в начальный момент времени уже ввели какое- то количество примеси.
Шприц можно описать δ-функцией.
Подогрели до 1000 .
Примесь будет расплываться и
распространяться слева направо.
.
Примесь будет расплываться и
распространяться слева направо.
Г.У.
x=0
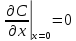 условие
отражения на левой границе
условие
отражения на левой границе
на правой границе:
x→∞
C(∞;t)=0
Решением этой краевой задачи является уравнение Гаусса:

Пример 2. Модель Дила – Гроува
Процессом термического окисления называют высокотемпературный процесс выращивания пленки SiO2 на кремниевой подложке в том случае, когда окислителем является либо О2, либо пары воды.

T=800 1200
1200
Если в печку закачать O2 либо пары H2O, пойдет химическая реакция:
Si + O2
 SiO2
либо
SiO2
либо
Si + 2H2O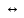 SiO2
+ 2H2
SiO2
+ 2H2
На пластине вырастит пленка

пленка называется термическим окислом (1000Å)
На
рисунке показана подложка кремния,
покрытая слоем, который находится в
контакте с газовой фазой. Окисляющие
элементы диффундируют из объема газовой
фазы на границу раздела газ-окисел
(поток J1), переносятся
через уже образованный окисел по
направлению к кремнию (потокJ2)
и реагируют на границе раздела фазSi-SiO2с кремнием (потокJ3).
Принимается, что каждая из стадий протекает со скоростью, пропорциональной концентрации окислителя. На первом этапе действует Закон Генри, на втором - закон Фика для диффузии, скорость на третьем этапе определяется скоростью химической реакции кинетики первого порядка по кислороду. Также подразумевается, что система находится в установившемся состоянии, т.е. переходный процесс не учитывается.
В условиях равновесия

|
|
|
|
 – поверхностная концентрация в окисле,
на внешней поверхности.
– поверхностная концентрация в окисле,
на внешней поверхности.
 – равновесная объёмная концентрация
в окисле.
– равновесная объёмная концентрация
в окисле.
|
|
|
|
 –концентрация окисляющего агента в
окисле вблизи границы раздела фаз
окисел-кремний.
–концентрация окисляющего агента в
окисле вблизи границы раздела фаз
окисел-кремний.
 –толщина окисла.
–толщина окисла.
|
|
|
|
 –концентрация скорости поверхностной
химической реакции окисления кремния.
–концентрация скорости поверхностной
химической реакции окисления кремния.

Nок – концентрация молекул окислителя в единице объема SiO2
Nок
 2,2
2,2
 1022
см-3
1022
см-3
закон Дила-Гроува:
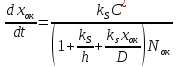
Первая форма записи закона Дила-Гроува:

где


 – параболическая константа,
– параболическая константа, – линейная константа.
– линейная константа.
при
 после интегрирования и преобразования
получаем вторую форму записи закона
Дила-Гроува:
после интегрирования и преобразования
получаем вторую форму записи закона
Дила-Гроува:

Введем константу:

 ,
,
Уравнени является обычным квадратный уравнением, его решением будет третья форма записи закона Дила-Гроува:

График кинетики окисления

I- участок начала роста;
II- линейный участок;
III- параболический участок.

В процессе термического окисления происходит следующая закономерность: на одну единицу объема расходуемого Si приходится 2,25 единицы выращенного окисла


Все многообразие процесса термического окисления модели Дила- Гроува описывается с помощью констант, которые зависят от Т по закону Аррениуса.
|
|
|
|
Чтобы описать процесс, необходимо задать 4 константы: С1, Е1, С2, Е2.
|
Тип окисления |
|
|
|
Сухое |
|
|
|
Влажное |
|
|
|
Пирогенное |
|
|
Пример 3. Модель процесса диффузии совместно с процессом термического окисления
Характерная особенность диффузионных процессов при термическом окислении Si заключается в том, что в этом случае область математического моделирования( область, где идет диффузия) изменяется со временем. И поэтому математическая задача получается, как задача с подвижной границей.
Межфазная граница Si–SiO2движется со скоростью, которая расходуется на толщину Si.
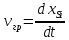

Величину xSi можно легко найти, если:
легко выразить через скорость роста толщины окисла, то есть свести к модели Дила – Гроува
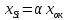 ;
;


При этом на движущейся межфазной границе происходит распределение легирующей примеси таким образом, что отношение концентрации в Si и в окисле SiO2будет постоянной в условиях квазиравновесия, и эта величина называется коэффициентом сегрегации.

Другим фактором определяющим распределение примесей на межфазной границе, является отношение коэффициентов диффузии

В общем случае, возможны следующие комбинации этих двух параметров
|
Варианты |
Примесь |
ms |
rD |
|
а. m>1,rD>1 |
P, As, Sb |
102 |
>103 |
|
б. m<1, rD>1 |
B |
0.1 |
>103 |
|
в. m>1, rD<1 |
Ga, In |
|
|
|
г. m<1, rD<1 |
Al |
|
|
Графически процесс сегрегации можно представить так:
а.


б.

в.

г.
В процессе термического окисления на межфазной границе происходит перераспределение примесей.
Чтобы избавиться от подвижной границы, нужно изменить начало координат, где граница будет неподвижной.
Перейдем к новой системе координат, введем новую переменную

y=0 неподвижная граница
Уравнение диффузии в Si

В равновесных условиях концентрация на межфазных границах

Изменение количества примеси, обусловлено диффузионным распределением примесей в прокисленном слое Si.
dQ- количество примеси в прокисленном слое Si
dQок- количество примеси в образовавшемся слое окисла
dQ- dQок=W dt
dt
dXок=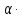 dXSi
dXSi
W=
(
краевое условие или условие
Аталлы-Таненбаума:
 (
(
Пример 4. Диффузионное расплывание неосновных носителей в эксперименте Хейнса - Шокли

Эксперимент, впервые доказавший существование тока неосновных носителей (дырочной проводимости в полупроводнике n-типа) в полупроводниках и позволивший измерить основные свойства дырок — скорость дрейфа и скорость диффузии.

где Pn- концентрация дырок в полупроводнике n-типа
Р0- равновесная концентрация дырок
Jp- плотность потока дырок
Gpи Rp- скорость генерации и рекомбинации дырок за счет теплового процесса
 р-
время жизни дырок
р-
время жизни дырок
3D

1D

Еслиполе отсутствуетЕ=0

Можно доказать, что концентрация избыточных дырок будет описываться как:


Q0- концентрация в моментt=0
Если поле существует Е 0
0
Нужно ввести новую переменную y, такую что

Уравнение диффузии, как модель подходит не только для описания самих процессов, но и для описания рекомбинации неосновных носителей заряда.



Анализ математической модели
Анализ модели математической задачи предполагает получение какой – либо предварительной информации об изучаемом явлении или процессе путем использования всех традиционных методик, применяемых физиками - теоретиками
А именно:
Проводится качественный анализ размерности
Осуществляется поиск частных решений, особенно в каких либо предельных случаях
С математической точки зрения на данном этапе необходимо:
сформировать задачу, как задачу математической физики
установить, имеет ли задача решения, если имеет, то сколько
уяснить качественную зависимость решения от параметров
разработка оптимального ( с вычислительной точки зрения) алгоритма нахождения искомых величин
Опыт показывает, что на предварительных этапах исследования математические бессмысленные модели возникают не так уж и редко. Поэтому любая модель должна быть проверена на корректность.
Модель корректна если:
она имеет решение
решение единственное
достаточно малому изменению начальных данных, соответствует достаточно малое значение решений ( решение непрерывно)
Эти условия гарантируют, что применение вычислительного алгоритма, обеспечит нахождение решения в пределах точности, задаваемой точностью исходных данных. Алгоритм должен быть устойчив.
Вычислительно неустойчивый алгоритм, в котором малое колебание исходных данных, приводит к значительным колебаниям условий задачи, считается неккоректным и не может быть использован в математическом моделировании ни при каких условиях.
Общая схема классификации модели
|
Критерий |
Вид модели |
Примечание |
|
Способ представления |
|
закон Ома; Закон Мура; статистика; в форме численной модели; |
|
Способ зависимости параметров |
|
зависят от времени и НЕ зависят от координаты; зависят от времени и координаты |
|
Фактор случайности |
|
не зависят от случайности;
учитывают случайность |
|
Уровень детализации |
|
механика сплошных сред (диф-ая модель); модель учитывает атомарно-молекулярное строение вещества |
|
Инерционность |
|
переменные не зависят от времени; зависят от времени |
В процессе построения и выбора модели, нужно четко определить факторы моделирования и ответить для себя на вопросы:
Что мы хотим моделировать
В каких условиях работает объект моделирования
С какой степенью точности модель должна отражать свойства реального объекта
Какой способ представления модели целесообразно принять
Как определить параметры модели
Вычислительный эксперимент
Вычислительный эксперимент– это численные эксперименты над математической моделью, которые состоят в том, что по одним параметрам и переменным вычисляют его другие параметры и характеристики, и на этой основе делаются выводы о свойстве изучаемого явления, процесса или объекта.
Основой вычислительного эксперимента является математическое моделирование, теоретической базой – прикладная математика, а технической базой- компьютер.
Вычислительный эксперимент, как новый вид теоретического исследования, оформился в отдельное научное направление во второй половине прошлого века, практически сразу после появления первых ЭВМ, на которых решались сложные математические задачи ядерной физики, баллистики и прикладной небесной механики.
В настоящее время значение вычислительного эксперимента только увеличивается. Прежде всего это связано с тем, что большинство применяемых теоретиками аналитических средств типа дифференциального и интегрального исчисления больше всего подходят для решения линейных задач. А реальное множество природных процессов и явлений описывает по своей физической сути нелинейными моделями, для которых нет аналитических решений. В этом случае вычислительный эксперимент является единственным способом для исследования нелинейных объектов и явлений.
Другая причина эффективности вычислительного эксперимента заключается в информационной сложности современных моделей, которые обладают многими степенями свободы и большим количеством переменных.
Использование вычислительного эксперимента при решении конкретных задач всегда имеет специфические особенности, но общая концепция повторяет уже рассматриваемые подходы, использованные при математическом моделировании, а именно:
производится выбор математического приближения и осуществляется постановка математической задачи
проводится предварительный анализ модели
осуществляется реализация вычислительной модели в виде вычислительного алгоритма на компьютере
предполагается, что исследователь напишет некую программу на языке высокого программирования
наработаны мощные вычислительные средства, благодаря которым, можно работать без углубления в программирование.
обработка и интерпретация результатов расчета, путем сопоставления с данными физического эксперимента и дальнейшее развитие используемой модели



















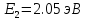
 103
103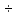 0.5
0.5
 10-3
10-3 10-3
10-3 10-3
10-3