Л.Р. №6. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ

ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ

Задание:

1. Составить двойственную задачу на основе исходной задач (см. лабораторную работу № 1.

2. Решить двойственную задачу симплекс-методом.

3. Решить двойственную задачу на компьютере.

4. Сравнить оптимальные решения, полученные на компьютере и симплекс - методом.

5. Сделать выводы.

Теория:

1. ПОНЯТИЕ ДВОЙСТВЕННОСТИ.

Описанные выше методы оценки чувствительности оптимального решения носят узкий характер, т. е. позволяют решать лишь частные задачи анализа на чувствительность моделей линейного программирования.

Понятие двойственности в теории линейного программирования возволяет унифицированным образом устанавливать взаимосвязи для всех методов анализа моделей на чувствительность. Для тех, кто не знаком с линейным программированием, понятие двойственности может показаться абстрактным и, следовательно, весьма непривычным. Только со временем это впечатление уступает месть пониманию исключительной важности и полезности этого понятия.

Мы рассмотрим двойственные задачи, оценки и их экономическую интерпретацию.

2. ОПРЕДЕЛЕНИЕ ДВОЙСТВЕННОСТИ.

С каждой задачей линейного программирования можно связать некоторую другую задачу, называемую двойственной. Первоначальную задачу при этом называют исходной. Рассмотрим двойственную задачу в общей постановке.

1. Пусть ограничения исходной задачи имеют вид:

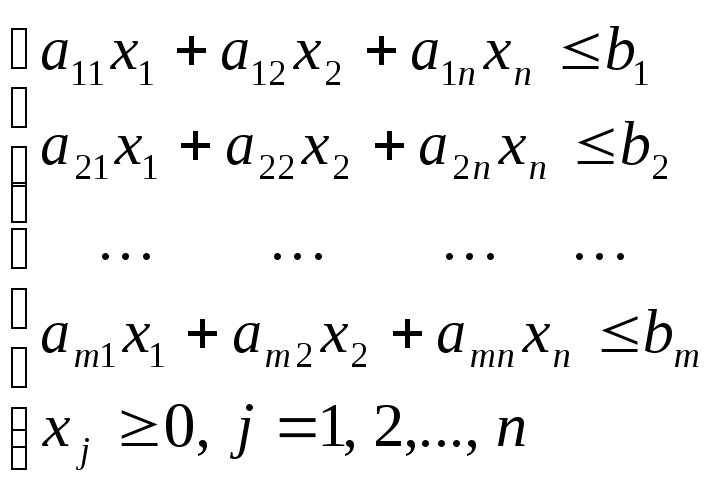
На множестве решений этой системы требуется максимизировать функцию

1. 

2. Двойственной для этой задачи будет задача с ограничениями

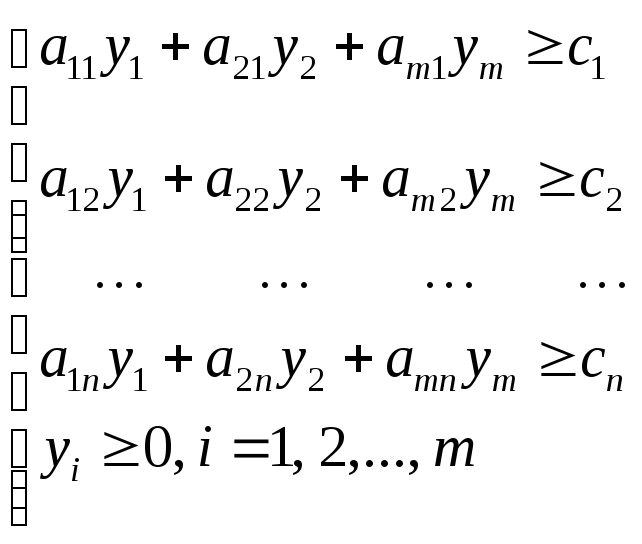
и минимизируется целевая функция

Сравнивая две задачи, нетрудно заметить, что:

а) матрица из коэффициентов при переменных в исходной задаче имеет вид:

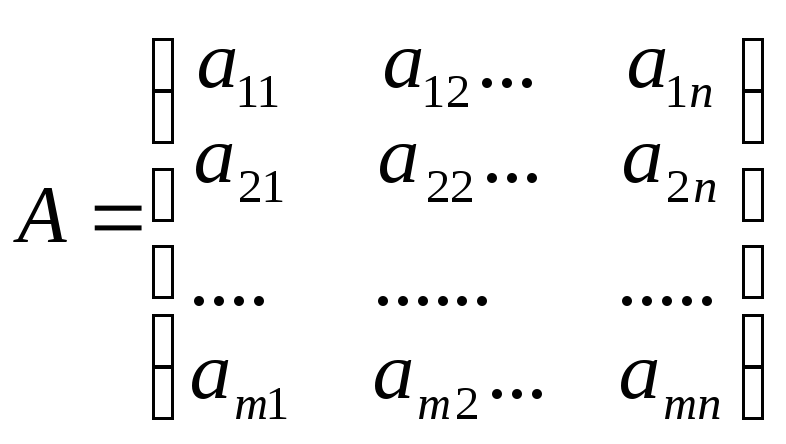
и аналогичная матрица в двойственной задаче имеет вид:

Как видно из сравнения, А^/ есть транспонированная матрица А, то есть i-я строка матрицы А является i-м столбцом матрицы А^/ и наоборот;

б) в исходной задаче n переменных x_j и m ограничений, в двойственной – m переменных y_i и n ограничений;

в) в правых частях систем ограничений каждой из задач стоят коэффициенты целевой функции, взятые из другой задачи;

г) в систему ограничений исходной задачи входят неравенства типа ≤ , причем в задаче требуется максимизировать целевую функцию F. В систему ограничений двойственной задачи входят неравенства типа ≥ , причем в двойственной задаче требуется минимизировать целевую функцию.

Исходная и двойственная ей задачи образуют пару задач, называемую в линейном программировании двойственной парой.

Замечание 1: за исходную задачу можно взять любую задачу из этой пары, для дальнейшего решения это несущественно.

Понятие о двойственной задаче позволит нам рассмотреть алгоритм решения транспортной задачи, как частный случай симплексного метода.

Грубо говоря, двойственная задача – это на 90° повернутая исходная задача.

Определение: Две задачи линейного программирования, удовлетворяющие указанным выше условиям, называются симметричными взаимно двойственными задачами.

Таким образом, каждой задаче линейного программирования можно поставить в соответствие двойственную задачу.

Замечание 2. Следует уточнить тип знака ограничений двойственной задачи. А именно, если x_j≥0, т.е. на j-ю переменную задачи наложено ограничение неотрицательности, то ограничение двойственной задачи имеет тип ≥.

Замечание 3. Если в исходной задаче ограничение имеет вид равенства, то на соответствующую этому ограничению переменную y_i в двойственной задаче не накладывается условие неотрицательности .

Если же ограничение имеет вид неравенства "≤", то соответствующая переменная y_i в двойственной задаче неотрицательна .

Рассмотрим эти утверждения на примере:

Прямая задача. Найти

При

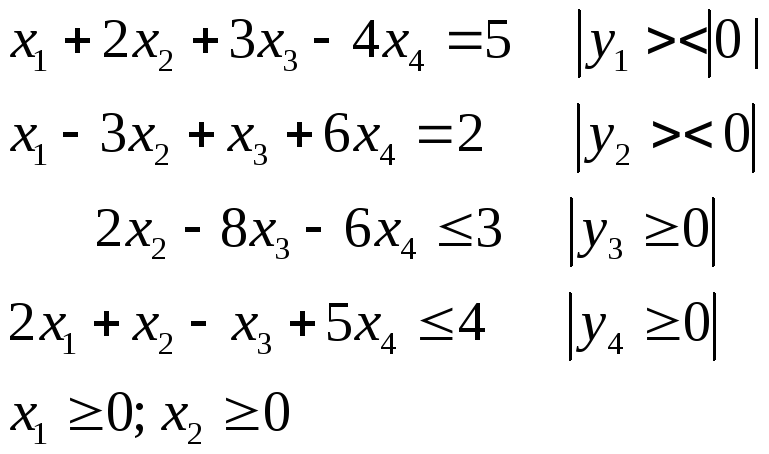
1. Введем переменные двойственной задачи y₁, y₂, y₃, y₄ (их столько, сколько ограничений в прямой задаче).

2. Запишем целевую функцию двойственной задачи:

3. Записываем систему ограничений двойственной задачи:

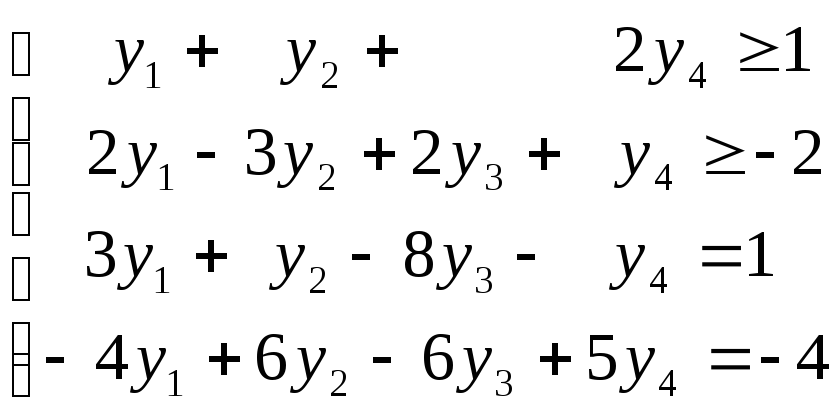
4. Вводим условия неотрицательности для переменных двойственной задачи:

- произвольные, т. к. в первых двух ограничениях стоят знаки "=";

т. к. в третьем и четвертом ограничениях исходной задачи стоят знаки "≤".

Замечание 4. В случае смешанных неравенств (≤ ≥) следует их привести к однородной форме (умножением соответствующих неравенств на –1).

3. СВОЙСТВА ДВОЙСТВЕННЫХ ЗАДАЧ (ОСНОВНЫЕ ТЕОРЕМЫ ДВОЙСТВЕННОСТИ)

Будем называть прямую (исходную) задачу Х-задачей, а двойственную к ней – Y-задачей.

Теорема 1 (Достаточный признак оптимальности)

Если есть допустимое решение Х-задачи, а есть допустимое решение Y-задачи и при этом , то есть оптимальное решение Х-задачи, а есть оптимальное решение Y-задачи.

Равенство целевых функций прямой и двойственной задач есть достаточное условие оптимальности двух допустимых решений пары симметричных двойственных задач.

Теорема 2 (Основная теорема двойственности)

а) Если одна из двойственных задач имеет оптимальное решение, то вторая также имеет оптимальное решение с тем же значением целевой функции.

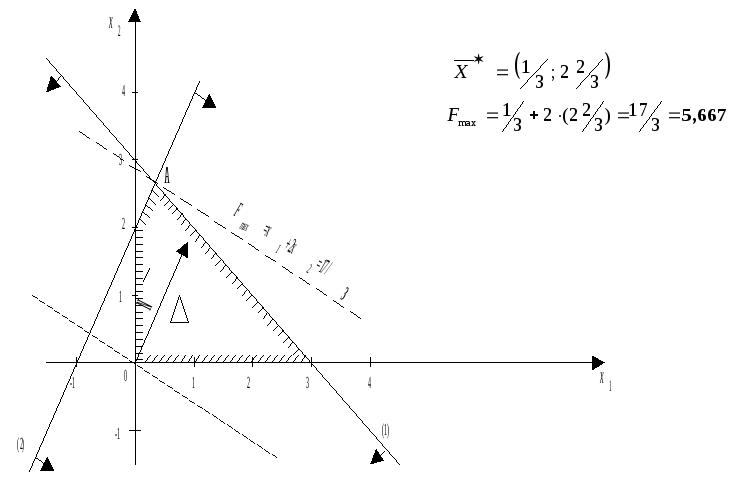
Вместо доказательства теоремы убедимся в ее справедливости на примере, который решим графическим методом.

Х – задача: найти

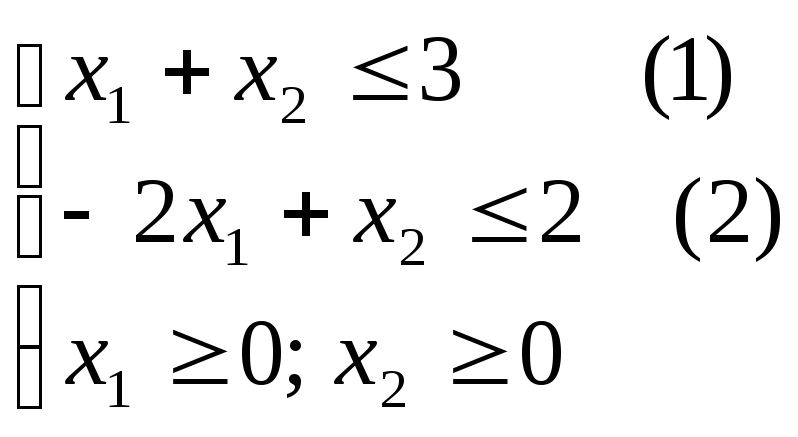
Y – задача:

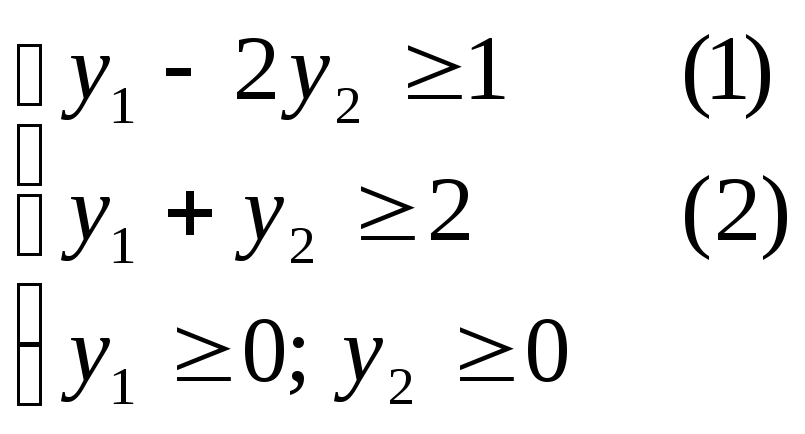
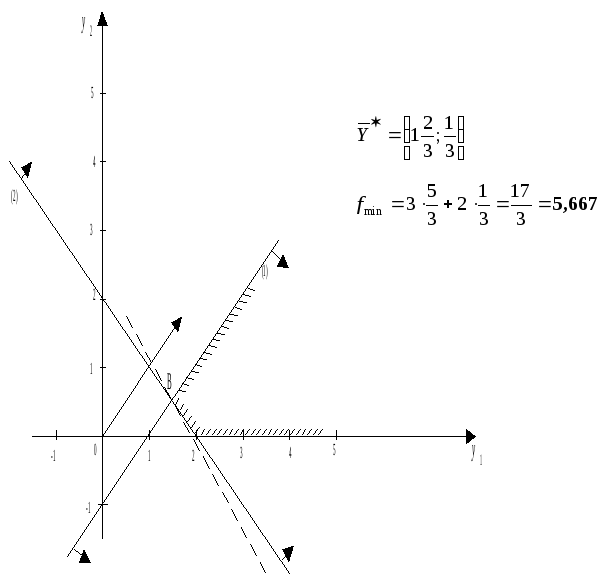
Таким образом

б) Если одна из пары двойственных задач не имеет оптимального решения из-за неограниченности целевой функции , то система ограничений второй задачи несовместна (пустое множество).

Пример:

Х – задача: найти

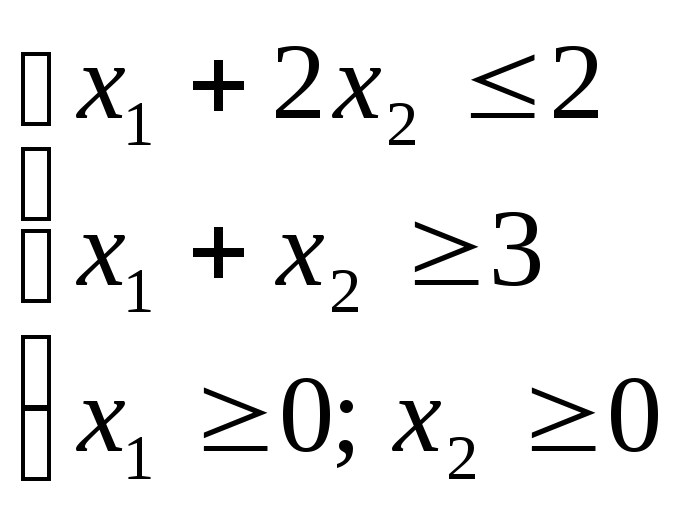
Множество решений является пустым, то есть система ограничений несовместна. Умножим второе неравенство на –1:

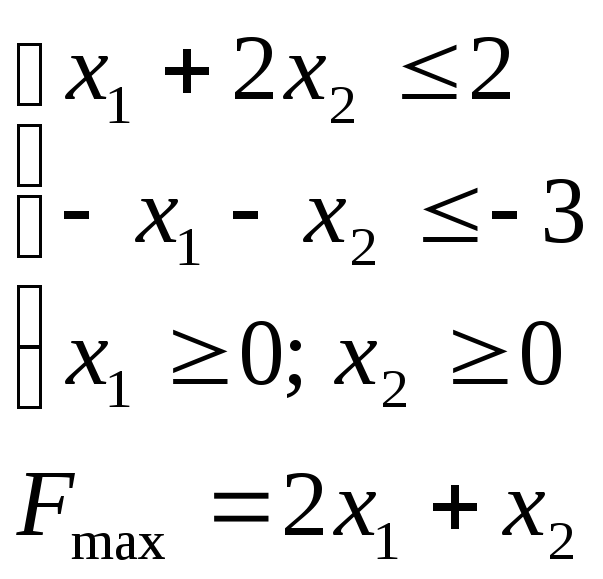
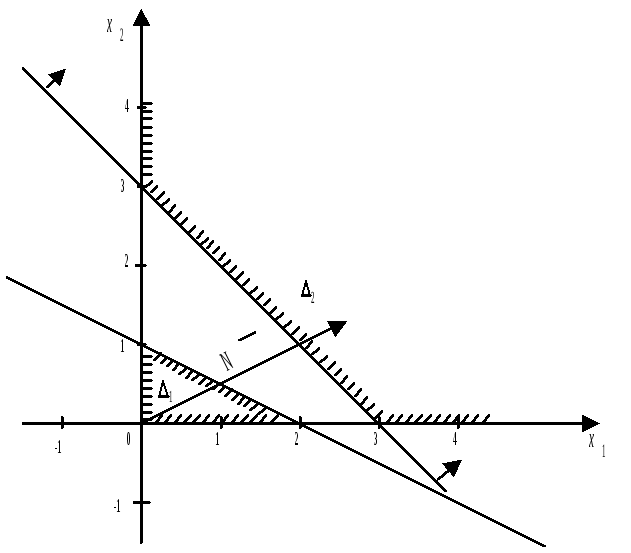
Y – задача:

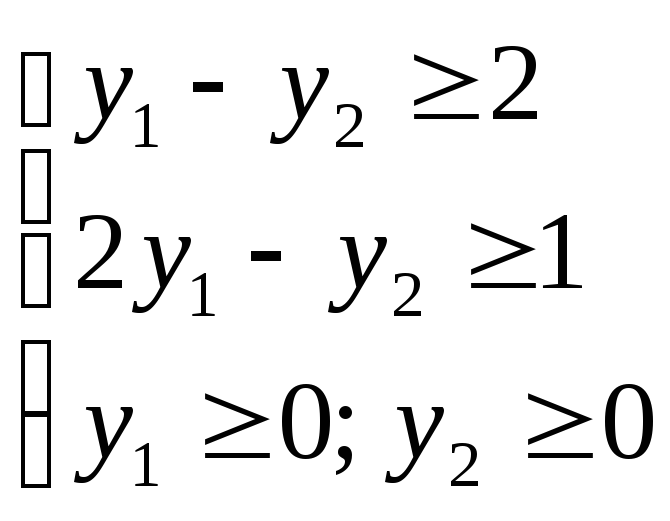
Здесь целевая функция не ограничена, т. е. , что доказывает утверждение теоремы.

Теорема 3 (Теорема о дополнительной нежесткости)

Пусть есть оптимальное решение Х-задачи. В этом случае должны выполняться условия дополнительной нежесткости:

• Если i-е ограничение Х-задачи оптимальным решением обращается в строгое равенство, то соответствующая переменная Y-задачи будет строго положительна ();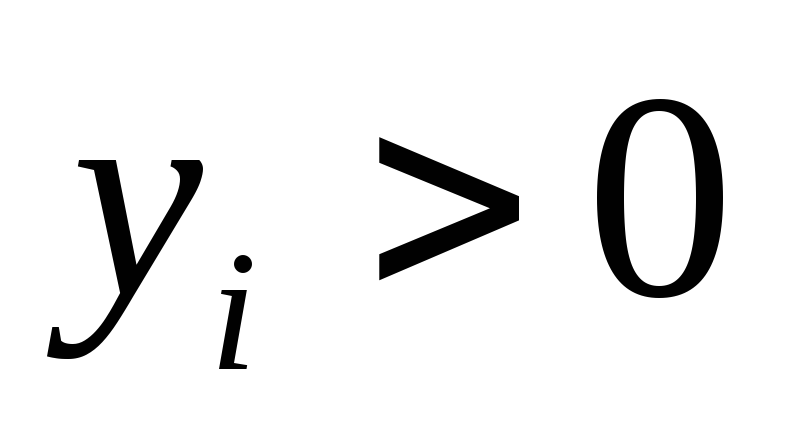

• Если i-е ограничение Х-задачи выполняется как строгое неравенство, то соответствующая переменная Y- задачи будет равна 0 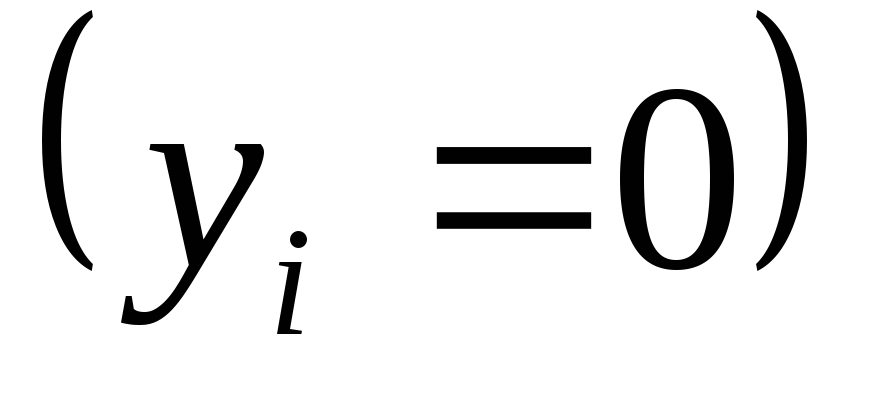и наоборот.

На основании теоремы 2, оптимальное решение Х-задачи однозначно определяет оптимальное решение Y-задачи. При этом симплексный алгоритм, примененнный к Х-задаче задает новый алгоритм преобрзований коээфициентов Y-задачи, который можно выписать в явном виде и применять для решения исходной задачи линейного программирования. Этот алгоритм называется двойственным симплекс-методом.