Информатика / Учебные_материалы / VBA / Задания по VBA 33

Правила оформления работы.

1. Программа составляется на языке Microsoft Excel Visual Basic в отдельном модуле, присоединенном к книге Microsoft Excel.

2. Программа должна обеспечивать ввод исходных данных и вывод результатов своей работы, используя лист Microsoft Excel.

3. Все используемые в программе переменные должны быть описаны в явном виде.

4. Все инструкции одинакового уровня вложенности должны иметь одинаковый отступ. Инструкции в каждом следующем уровне вложенности должны иметь отступ больше, чем в предыдущем.

5. Для проверки работоспособности программы должен быть придуман подходящий пример.

6. Выполненная работа (книга Microsoft Excel) должна быть сохранена в рабочей папке студента.

7. Блок схема, текст программы, исходные данные примера и результаты работы программы должны быть оформлены в тетради.

Пример оформленной работы

В интервале [] задана функция . Методом трапеций найти значение интеграла этой функции на заданном промежутке с заданной точностью . Суть метода заключается в следующем:

Промежуток интегрирования делится точками на заранее заданное равных частей (длина каждой равна ). Для единообразия полагается и . Приближенное значение интеграла определяется по формул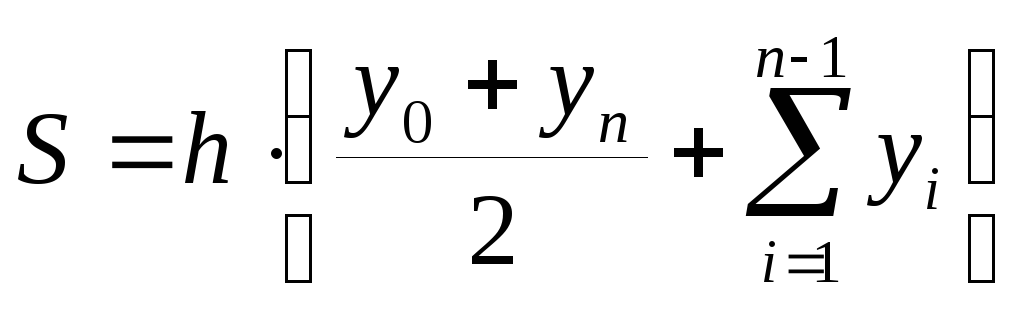е , где . После чего число разбиений увеличивается (например, в два раза). Процесс повторяется заново до тех пор, пока очередное рассчитанное значение интеграла не станет отличаться от предыдущего меньше, чем на заданную величину .

В интервале [] задана функция . Методом прямоугольников найти значение интеграла этой функции на заданном промежутке с заданной точностью . Суть метода заключается в следующем:

Промежуток интегрирования делится точками на заранее заданное равных частей (длина каждой равна ). Для единообразия полагается и . Приближенное значение интеграла определяется по формуле , где . После чего число разбиений увеличивается (например, в два раза). Процесс повторяется заново до тех пор, пока очередное рассчитанное значение интеграла не станет отличаться от предыдущего меньше, чем на заданную величину .

Для полинома -ой степени вида заданы коэффициенты . Преобразовать этот полином в многочлен вида , т.е. получить коэффициенты . Для этого использовать следующий алгоритм.

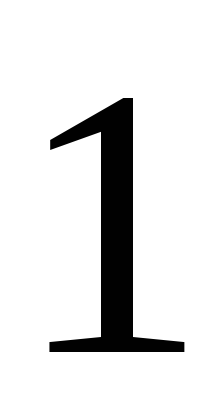1. Положить равным , а 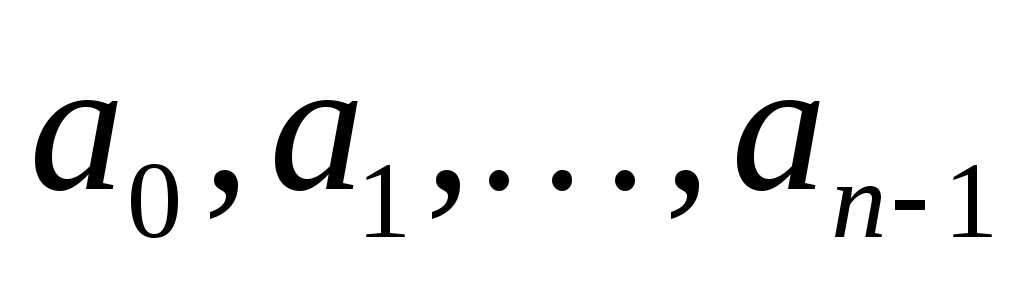равными 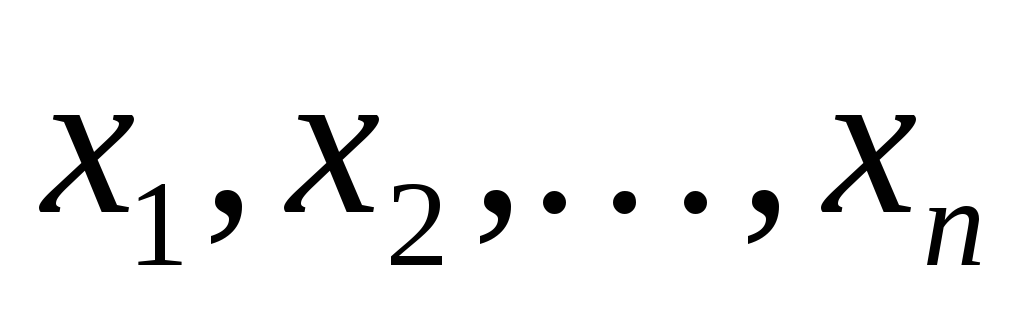соответственно.

2. Для всех от до 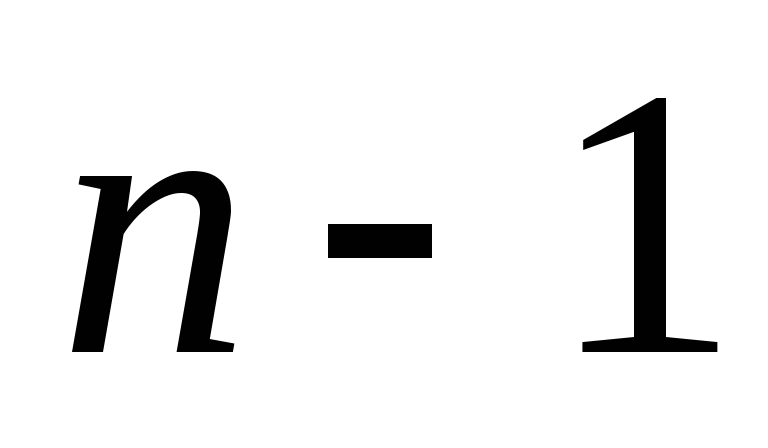выполнить следующий шаг.

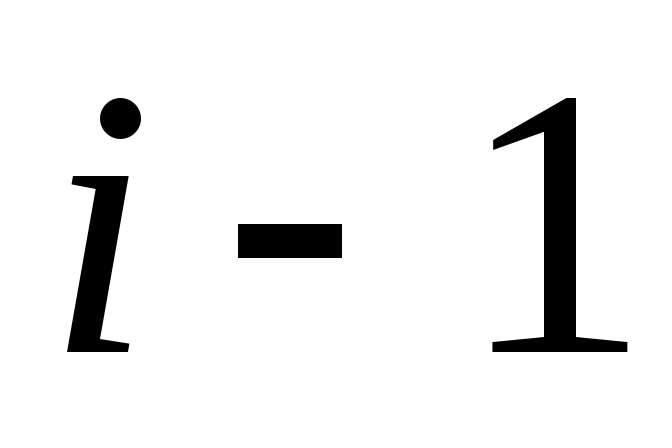3. Положить . Для всех от до выполнить следующий шаг.

4. Увеличить на , после чего умножить на .

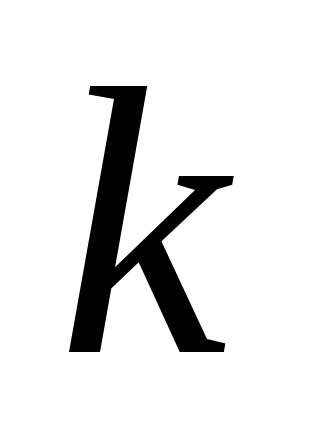Для заданного уравнения определено начальное приближение его корня . Уточнить корень данного уравнения методом переменного шага, суть алгоритма которого состоит в следующем:

Производится приращение начального приближения на величину заранее заданного шага до тех пор, пока значение функции в очередной точке не изменит знак. После чего шаг уменьшается в несколько раз (например, в три раза) и берется с противоположным знаком (т.е. ). Процесс повторяется заново до тех пор, пока не выполнится очередная серия приращений с шагом, абсолютное значение которого не превосходит заданную величину (точность локализации корня).

В процессе уточнения корня подсчитать количество обращений к функции , которое должно быть сведено к минимуму.

Выяснить, является ли заданный квадрат размером магическим. Магическим квадратом называется квадратная матрица, в которой расположены числа от до таким образом, что суммы чисел в любой строке, в любом столбце и по диагоналям равны.

Дано натуральное нечетное . Построить магический квадрат размером (квадратная матрица, в которой расположены числа от до таким образом, что суммы чисел в любой строке, в любом столбце и по диагоналям равны). Для построения использовать следующее соотношение:

, где - элемент матрицы; ; .

Координаты -ого элемента матрицы рассчитываются по формулам:

,

,

где коэффициенты и находятся в интервале от до и удовлетворяют условию:

.

Вычислить периметр и площадь многоугольника с координатами вершин . Ниже приводятся необходимые для расчета формулы.

Площадь многоугольника: , где

Расстояние между двумя точками:

Для заданных действительных (причем , ) найти значения функции (), если функция имеет следующий вид:

Значение функции считать полученным, если абсолютное значение очередного прибавленного слагаемого не станет меньше заданной величины . Во время расчетов каждого слагаемого не использовать операцию возведения в степень.

Заданное натуральное число , значения которого находятся в диапазоне от 1 до 999 представить в текстовой форме. Например: 23 = “двадцать три”.

В обращении имеются монеты достоинством , причем , (). Разменять заданную сумму наименьшим количеством монет (указать общее количество монет и сколько монет каждого достоинства будут участвовать в размене).

Заданы две матрицы и . Получить третью матрицу путем перемножения этих двух матриц по правилам матричной алгебры.

В заданном интервале натуральных чисел от до найти такие, где сумма всех цифр на нечетных местах равняется сумме цифр на четных. Такому условию удовлетворяет, например, число 2367541 (2+6+5+1=3+7+4).

В группе студентов из человек проведена аттестация по дисциплинам. Максимальные рейтинги дисциплин равны соответственно. Определить суммарные рейтинги для каждого студента, в масштабе от до . Определить “лучшего” и ”худшего”, в смысле суммарного рейтинга, студентов. Обеспечить вывод порядковых номеров этих студентов по списку, их оценок по каждой дисциплине и суммарных рейтингов.

Среди натуральных чисел от 1 до найти такие числа, значения которых равны сумме факториалов своих цифр. Например, в такую группу чисел не попадет число 2401, так как: .

В заданной матрице размером () поменять местами строки с номерами и , где и являются координатами наибольшего по модулю элемента матрицы.

Задана последовательность из натуральных чисел, каждое из которых находится в интервале от до включительно. Построить упорядоченную последовательность этих чисел в порядке убывания.

Вычислить значение числа по следующей формуле:

Вычисление прекратить, если модуль очередного слагаемого отличается от предыдущего меньше чем на заданное число . Определить, сколько для этого потребовалось слагаемых.

Для заданного найти все последовательности натуральных чисел , где (), для которых сумма всех чисел каждой последовательности равняется их произведению.

Для заданной квадратной матрицы размером определить норму матрицы:

и максимальные суммы модулей элементов строки и столбца:

, где , ,

, где , .

По заданной матрице размером получить матрицу путем вычеркивания из исходной матрицы строки с номером и столбца с номером , где и являются координатами наименьшего по модулю элемента матрицы.

В заданном диапазоне от 1 до найти все простые числа (числа, которые делятся нацело только на единицу и на само себя). Для проверки очередного числа используйте уже найденные простые числа. Т.е. используйте следующее свойство простых чисел: число является простым, если оно не делится нацело ни на одно простое число из диапазона от до .

Заданы прямоугольников, каждый из которых определяется координатами противоположных вершин (), а стороны параллельны (перпендикулярны) осям координат.

Составить список прямоугольников, которые не пересекаются ни с одним другим прямоугольником. Для каждой позиции списка указать порядковый номер прямоугольника и координаты его вершин. Список должен выглядеть следующим образом:

№
1
2
…

При составлении списка ни одна пара прямоугольников не должна проверяться на пересекаемость дважды.

Для заданных действительных найти значения функции (), если функция имеет следующий вид:

Значение функции считать полученным, если абсолютное значение очередного прибавленного слагаемого не станет меньше заданной величины . Во время расчетов каждого слагаемого не использовать операцию возведения в степень и не вычислять значение факториала каждый раз заново.

Дано натуральное нечетное . Построить магический квадрат размером (квадратная матрица, в которой расположены числа от до таким образом, что суммы чисел в любой строке, в любом столбце и по диагоналям равны). Для построения использовать следующее соотношение:

, где - элемент матрицы; ; .

Значение для очередного элемента матрицы рассчитывается по формуле:

где параметры и определяются следующем образом:

1. Для случая, когда значения координат 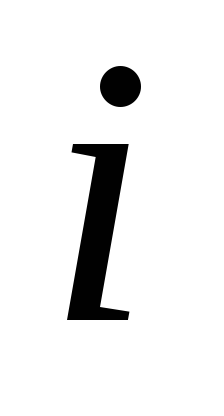и являются одновременно четными или нечетными числами:

, .

2. В противном случае:

,

Задана матрица размером . Транспонировать данную матрицу (получить матрицу путем замены каждой ее строки столбцом с тем же номером).

Задана последовательности действительных чисел , значения которых могут повторяться. Составить список значений и их количества, которые встречаются в данной числовой последовательности.

Заданы окружностей, каждая из которых определяется координатами центра и радиусом (). Составить список пар пересекающихся окружностей, в котором для каждой пары указать порядковые номера окружностей, их координаты центра и радиусы. Список должен выглядеть следующим образом:

№
1
2
…

В списке не должно встречаться одинаковых пар окружностей.

Задана квадратная матрица размером с ненулевыми элементами главной диагонали (, ) и вектор столбец длиной . Получить квадратную матрицу размером , и вектор столбец длиной , элементы которых определяются следующим образом:

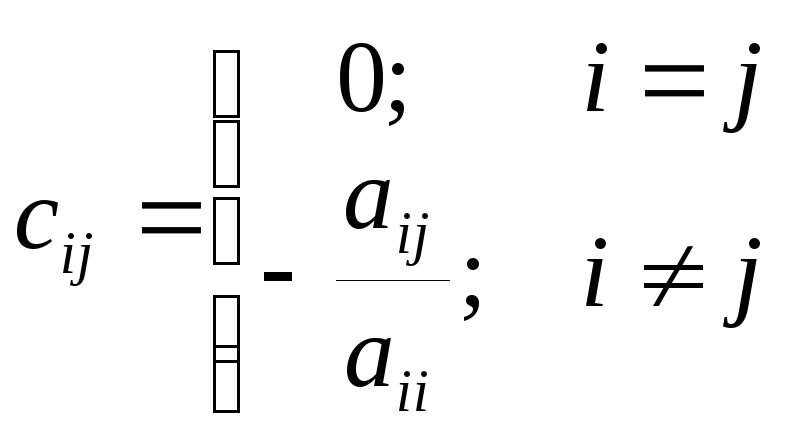, , где .

Известно, что один из корней заданного уравнения находится в интервале от до , причем значения функции на концах этого интервала имеют разные знаки (). Уточнить корень методом половинного деления исходного интервала, суть алгоритма которого состоит в следующем:

Рассматриваются два меньших интервала [] и [], где - середина интервала []. В качестве нового интервала [] берется тот, на концах которого функция меняет знак (т.е. интервал, содержащий корень). Данный процесс повторяется заново до тех пор, пока длина интервала [] не станет меньше заданной величины (точности локализации корня). Корнем уравнения посчитанной с заданной степенью точности считается одна из границ интервала [].

В процессе уточнения корня подсчитать количество обращений к функции , которое должно быть сведено к минимуму.