6.3. Истечение жидкости через большие отверстия

Отверстия являются большими, если давление в пределах их живого сечения переменно, а скорость увеличивается по мере удаления от верхней кромки отверстия. Рассмотрим большое отверстие произвольной формы в тонкой стенке (рис. 6.6). Напор по верхней кромке отверстия , по нижней - . Выделим в большом отверстии горизонтальную полоску высотой , которую будем считать как площадь малого отверстия. Напор для такого отверстия полагаем постоянным и равным Н. Элементарный расход, проходящий через эту горизонтальную полоску,

, (6.19)

где - коэффициент расхода условного малого отверстия в виде полоски;Н - напор для малого отверстия.

Полагаем, что для всех узких горизонтальных полосок, на которые разбивается большое отверстие.

Расход, проходящий через все горизонтальные полоски, получим, интегрируя (6.19), а постоянные величины выносим за знак интеграла:

. (6.20)

При нахождении расхода по формуле (6.20) необходимо знать функциональную зависимость переменной ширины от высоты большого отверстия.

Рис. 6.6. Истечение из большого отверстия произвольной формы

Рассмотрим частный случай большого отверстия прямоугольной формы (рис. 6.7). Ширина отверстия равна . Расход жидкости для прямоугольного отверстия согласно зависимости (6.20) после интегрирования

. (6.21)

Расход жидкости может быть также вычислен, принимая напор истечения относительно центра тяжести большого отверстия .

Рис. 6.7. Истечение из большого прямоугольного отверстия в тонкой стенке

- расстояние от свободной поверхности жидкости в резервуаре до центра тяжести большого отверстия. Тогда

(6.22)

или

, (6.23)

где - коэффициент расхода большого отверстия.

Для прямоугольного отверстия площадь отверстия

,

где , - высота и ширина отверстия.

Следует отметить, что коэффициент расхода зависит от размеров, формы отверстия, обработки кромок отверстия, влияния стенок на сжатие струи, напора и т.д.

Ориентировочно при определении расхода можно принимать при совершенном сжатии и- при несовершенном.

6.4. Истечение жидкости через насадки

Насадком называют патрубок относительно небольшой длины, имеющий различные поперечные формы сечения.

Насадки принято делить на основные три типа: цилиндрические, конические и коноидальные.

Цилиндрические насадки

Цилиндрические насадки могут быть внешними или внутренними (рис. 6.8).

На входе в насадки имеются достаточно острые кромки. Внешний насадок присоединяется к наружной стороне резервуара к отверстию того же диаметра под прямым углом. Длина патрубка составляет порядка . В результате обтекания острых кромок на входе в насадок происходит сжатие струи внутри насадка, как это имеет место при истечении из малого отверстия. За сжатым сечением площадью следует расширение струи до поперечного сечения самого насадка. Непосредственно в зоне сжатого сечения возникает вихреобразование в виде кольцевой водоворотной области. Скорость струи в сжатом сечении существенно больше скорости на входе в насадок, в результате в этой области давление становится меньше атмосферного, т.е. создается вакуумметрическое давление.

Рис. 6.8. Цилиндрические насадки: а - внешний; б - внутренний

Максимальное вакуумметрическое давление будет иметь место непосредственно в сжатом сечении. На границе водоворотной области ближе к выходу из насадка . Все вышеизложенное можно доказать, используя уравнение Бернулли. Для получения формулы расхода для цилиндрического насадка рассмотрим схему, представленную на рис. 6.9.

Напишем уравнение Бернулли относительно плоскости сравнения 0-0, проходящей по оси насадка. Сечение 1-1 принимаем по свободной поверхности жидкости в резервуаре, а сечение 3-3 - на выходе из насадка. Давление на поверхности жидкости в резервуаре , а истечение жидкости осуществляется в атмосферу:

. (6.24)

Скоростью движения в резервуаре пренебрегаем. Принимаем .

; ;;;.

Рис. 6.9. Истечение из внешнего цилиндрического насадка

Гидравлические потери на участке от сечения 1-1 до 3-3 с учетом потерь по длине

.

В результате после соответствующих подстановок получим

, (6.25)

где - суммарный коэффициент сопротивления на участке от 1-1 до3-3.

Скорость окончательно представляется в известном ранее виде

,

где - коэффициент скорости насадка;

.

Расход жидкости, проходящий через насадок,

. (6.26)

Так как насадок не имеет сжатия на выходе из него, то , и для цилиндрического насадка коэффициент расхода насадкаравен коэффициенту скорости:

. (6.27)

В результате проведения опытов при длине насадка и достаточно больших значениях числасумма коэффициентовв среднем, как показали численные расчеты, равна

.

Для цилиндрического насадка коэффициент скорости

.

Если длина насадка , следует учитывать потери напора по длине. Суммарный коэффициент сопротивлений

. (6.28)

Так как , то коэффициент расхода при

. (6.29)

В результате увеличения скорости в сжатом сечении возрастает вакуумметрическое давление. За счет разности атмосферного и вакуумметрического давлений воздух может поступать в насадок через выходное сечение. В результате поток будет полностью отрываться от стенок насадка и будет происходить срыв вакуума. Насадок будет работать, как при истечении из отверстия. Расход, проходящий через насадок, уменьшится и будет соответствовать расходу, как из отверстия в тонкой стенке.

Найдем значение вакуумметрического давления, имеющего место в сжатом сечении. Напишем уравнение Бернулли для сечений 2-2 (сжатое сечение С-С) и 3-3 на выходе из насадка. Плоскость сравнения проходит по оси насадка (см. рис. 6.9).

, (6.30)

где ; - абсолютное давление, ;.

Принимаем ;; ;-гидравлические потери на участке от сечения 2-2 до 3-3.

Потери напора по длине принимаем .

Потери напора приближенно определяем, как потери напора на внезапном расширении, .

После подстановок получим

. (6.31)

Вакуумметрический напор

.

Тогда согласно (6.31)

. (6.32)

Коэффициент внезапного расширения .

Согласно уравнению неразрывности выразим скорость в сжатом сечении через V:

, ,

тогда

, (6.33)

где - коэффициент сжатия.

В результате вакуумметрический напор будет

. (6.34)

Выражение, стоящее перед скоростным напором , преобразуем к виду

. (6.35)

Подставив (6.35) в (6.34), получим

(6.36)

Выразим скорость V через напор H:

.

Заменим в зависимости (6.36) скорость, откуда вакуумметрический напор

. (6.37)

Как уже отмечалось ранее, для внешнего цилиндрического насадка коэффициент скорости . Коэффициент сжатия струи в насадке принимаем. Согласно вышеизложенному определим вакуумметрический напор по уравнению (6.37) с учетом напораH:

.

Опытами было установлено, что срыв вакуума происходит, если максимальный вакуумметрический напор м и начинается подсасывание воздуха через выходное отверстие насадка, а истечение жидкости осуществляется аналогично отверстию в тонкой стенке.

Предельное значение напора H, при котором истечение из насадка будет работать без срыва вакуума,

м.

Таким образом, истечение струи из внешнего цилиндрического насадка полным сечением будет происходить при м и предельном напорем при длине насадка.

Внутренние цилиндрические насадки

Цилиндрический насадок, находящийся внутри резервуара, называется внутренним насадком (см. рис. 6.8). На входе в такой насадок поток (струя) претерпевает большее сжатие, чем это имеет место во внешнем насадке. Причиной этого является обтекание потоком входного отверстия насадка с относительно малой толщиной по кромке . Сопротивления на входе, связанные с деформацией потока, зависят от относительной толщины передней кромки насадка.

Установлено, если , то истечение происходит аналогично истечению из малого отверстия, т.е. струя, отрываясь от кромок, не касается стенок насадка. При получены следующие значения коэффициентов: коэффициент скорости; коэффициент расхода; коэффициент сжатия. Значения коэффициентов,значительно меньше, чем для отверстия в тонкой стенке.

В случае увеличения длины насадка () внутренний насадок работает, как правило, полным сечением; при имеем;.

Нецилиндрические насадки

Конические насадки. К коническим насадкам относятся сходящиеся и расходящиеся насадки (рис. 6.10). Сходящийся насадок имеет форму усеченного конуса, образующие которого направлены к выходному отверстию. В таких насадках деформация потока достаточно мала, водоворотная вихревая область незначительна и потери напора существенно меньше, чем у цилиндрического насадка.

Рис. 6.10. Конические насадки: а - сходящийся (сужающий); б - расходящийся

Опытами установлено, что коэффициент расхода для конических насадков достигает максимальных значений при угле конусности, а коэффициент сжатия на выходе. Увеличение углаприводит к уменьшениюи увеличению сжатия струи на выходе. Для квадратных и прямоугольных форм сечения насадков угол конусности принимается, при этом коэффициент расхода.

Применение сужающих насадков позволяет получить компактную струю с достаточно большой скоростью истечения. Насадки такого типа применяются в различных струйных аппаратах, гидромониторах, пожарных наконечниках и т.д.

У расходящихся насадков происходит расширение сечения под углом конусности . В таком насадке наблюдается достаточно большой отрыв потока от входных кромок, в результате водоворотная область увеличивается и, следовательно, площадь сжатого сечения уменьшается.

Вакуумметрический напор в сжатом сечении становится несколько больше, чем у внешнего цилиндрического насадка, с увеличением угла конусности .

Диаметр выходного отверстия насадка при диаметре входного d

. (6.38)

Увеличение размеров насадка, т.е. ,D, в результате возрастания площади выходного отверстия обусловливает уменьшение коэффициента расхода .

Угол конусности рекомендуется устанавливать .

Опытами установлено, что при угле и значения .

Расход, проходящий в насадке, определяется по следующей формуле:

, (6.39)

где - площадь выходного отверстия.

При сравнении внешнего цилиндрического и расходящегося насадков при одинаковых входных отверстиях расход последнего будет существенно большим.

Расходящиеся насадки используются в пожарной технике для распыления с помощью пенных огнетушителей, при увлажнении почв, в водоструйных насосах, гидроэлеваторах, в городских и парковых фонтанах для создания струи разных видов и форм и т.п.

Коноидальный насадок представляет собой улучшенный тип сходящегося насадка, у которого форма входного отверстия имеет плавное очертание. Плавное входное отверстие не вызывает отрыва потока от стенок, практически устраняет сжатие струи внутри насадка, в результате этого потери напора сводятся к минимуму (рис. 6.11). Значения коэффициентов и зависят от формы скругления, шероховатости внутренней поверхности насадка. Обычно и в расчетах принимаются равными 0,950,98.

Рис. 6.11. Насадки с плавным входом: а - сходящийся; б - расходящийся

♦ Пример 6.3

Резервуар разделяется на две части вертикальной стенкой, в которой имеется круглый конусный насадок мм. Глубина воды в левой части резервуарам. Расход, протекающий через отверстие,л/с. Определить глубину воды в правой части резервуараи диаметр малого отверстия. Расстояние от дна резервуара до осей отверстия и насадка м. Уровни воды в резервуарах постоянны (рис. 6.12).

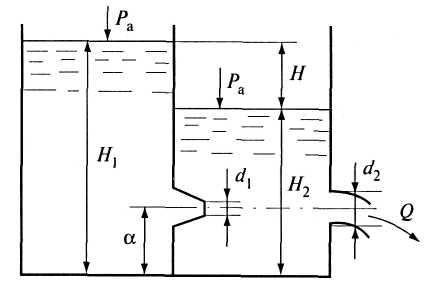
Рис. 6.12. К примеру 6.3

Принимаем коэффициенты расхода отверстия , конусного насадка - . Расходы истечения из насадка и отверстия постоянны .

Истечение из насадка происходит при напоре .

Расход .

В данном уравнении — неизвестная величина.

Определим из уравнения расхода , возведя в квадрат и выделяя :

м.

Напор при истечении из малого отверстия

м.

Расход из малого отверстия

.

Диаметр отверстия

м.