133

Задания для самостоятельной работы студентов

1. Зависимость пройденного телом пути от времени задана уравнением S = 0,1t² + 0,03t³. Определить момент времени, в который ускорение тела а = 2 м/с².

Ответ: t = 10 с.

2. При горизонтальном ветре, скорость которого υ₁ = 10 м/с, капли дождя падают под углом ₁ = 30^ к вертикали. При какой скорости ветра капли будут падать под углом ₂ = 60^ к вертикали?

Ответ: υ₂ = 30 м/с.

3. Струя воды при поливе из шланга вылетает со скоростью υ_ = 9 м/с под углом  = 45^ к горизонту. Найти, на каком расстоянии можно обеспечить полив растений, если время движения струи до поливной точки t = 1,3 с.

Ответ: S = 8,2 м.

4. В ботаническом саду из семян выращивают ели “колючие”. От года к году приросты сеянцев увеличивались. За третий год прирост одного из них составил 4 см. Считая процесс роста равноускоренным, определить прирост растения за пятый год. Через сколько лет его высота составит h = 0,5 м?

Ответ: h₅ = 7,2 см; t = 8 лет.

5. Частота вращения колеса радиусом R = 2 м при равнозамедленном торможении уменьшилась от n₁ = 300 мин^-1 до n₂ = 180 мин^-1 за время ∆t = 1 мин. Определить угловое ε и тангенциальное а_ ускорения точек обода колеса.

Ответ: ε = 0,21с^-2; а_ = 0,42 м/с².

6. Зависимость угла поворота от времени для колеса радиусом R = 10 см задана уравнением φ = 2t²+t³. Найти угловую  и линейную υ скорости точек, лежащих на ободе колеса, в момент времени t = 2 с.

Ответ:  = 20 рад/с; υ = 2 м/с.

7. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а_ = 5 см/с². Через какой промежуток времени после начала движения нормальное ускорение а_n будет равно тангенциальному а_?

Ответ: t = 2 с.

8. Колесо радиусом R = 10 см вращается с угловым ускорением ε = 3,14 с^-2. Найти для точек обода колеса к концу первой секунды: угловую скорость ; линейную скорость υ; тангенциальное а_ и нормальное а_n ускорения.

Ответ: = 3,14 рад/с; υ = 0,314 м/с;

а_ = 0,314 м/с²; а_n = 0,986 м/с².

9. Трос подъёмного устройства выдерживает силу натяжения F_нат = 8,5 кН. Определить массу груза, которую он может поднять с ускорением а = 2,45 м/с².

Ответ: m = 694 кг.

10. Два тела массами т₁ = 100 г и m₂ = 150 г висят на нерастяжимой и невесомой нити, перекинутой через неподвижный блок. Определить скорость тел через 1 с после начала их движения.

Ответ: υ = 2 м/с.

11. Трактор, движущийся со скоростью υ₀ = 43 км/ч, останавливается за время ∆t = 8 c. Масса трактора т = 1 т. Вычислить силу торможения и тормозной путь.

Ответ: F_тр = 1,5 кН; S = 48 м.

12. Спиленное дерево массой m = 100 кг с помощью лебёдки равномерно втаскивают на плоскую поверхность грузовой платформы трелевочного трактора, которая наклонена под углом  = 45^ к горизонту. Динамометр, контролирующий натяжение троса лебёдки, показывает, что сила F_нат = 850 Н. Найти коэффициент трения скольжения между бревном и платформой.

Ответ:  = 0,2.

13. Автомобиль массой m =1,5 т движется по выпуклому мосту со скоростью υ = 70 км/ч. Определить силу давления на мост в верхней его части, если радиус кривизны моста R= 250 м.

Ответ: F = 12,45 кН.

14. Давление в каждой из четырёх шин автомобиля Р = 0,2 МПа. Каков вес автомобиля, если площадь соприкосновения шины с грунтом S = 500 см²?

Ответ: F = 40 кН.

15. В лифте, движущемся вниз с ускорением а = 2,3 м/с², на пружинных весах находится тело массой m = 20 кг. Определить показание весов.

Ответ: P = 150 Н.

16. Тело находится на наклонной плоскости, угол наклона которой  = 45^. На сколько процентов вес тела на наклонной плоскости меньше, чем на горизонтальной?

Ответ: ∆Р/Р_гор = 30%.

17. Для направленного роста растений в космосе предполагается применять вращающиеся оранжереи. Вычислить частоту и период вращения оранжереи, необходимые для получения центробежной силы инерции F = 0,3mg, на расстоянии R = 25 м от оси.

Ответ:  = 0,055 с^-1; Т = 18 с.

18. Определить ускорение силы тяжести на поверхности Земли. Землю считать однородным шаром радиусом R = 6,37 Мм и плотностью  = 5,5 г/см³.

Ответ: g = 9,78 м/с².

19. Определить период обращения спутника Земли, движущегося на высоте h = 10⁴ км. Радиус Земли R = 6,37 Мм, масса Земли m = 5,98∙10²⁴ кг.

Ответ: Т = 5,7 ч.

20. Зная среднюю скорость движения Земли вокруг Солнца υ₁ = 30 км/с, определить, с какой средней скоростью υ₂ движется малая планета вокруг Солнца, если радиус её орбиты в 4 раза больше радиуса орбиты Земли.

Ответ: υ₂ = 15 км/с.

21. Деревянный брус, имеющий форму куба, опрокидывают через ребро. Во сколько раз опрокидывающая сила, приложенная горизонтально к середине верхнего ребра, меньше силы тяжести?

Ответ: в 2 раза.

22. Чему равна горизонтальная сила, которую нужно приложить к верхней точке колеса, чтобы закатить его на ступеньку высотой, равной радиусу колеса? Масса колеса m = 65 кг. Как изменится эта сила, если её приложить под углом  = 45^ к первоначальному направлению в той же точке колеса?

Ответ: F_гор1 = 650 Н; уменьшится в 1,4 раза.

23. Точка опоры однородной доски массой m = 10 кг находится на расстоянии ⅓ её длины. Какую силу F, перпендикулярную доске, надо приложить к её короткому концу, чтобы удержать доску в равновесии?

Ответ: F = 50 Н.

24. От однородного бревна отрезали конец длиной l₁ = 40 см. Куда и на сколько переместился центр тяжести? На сколько процентов изменился вес, если первоначальная длина составляла l = 2 м?

Ответ: Центр тяжести сместился на 20 см; 20 %.

25. Молотильный барабан, имеющий момент инерции J = 50 кг∙м², вращается с частотой n₁ = 10 c^-1. Какой момент силы М следует приложить, чтобы частота вращения барабана увеличилась за время ∆t = 20 c в 2 раза?

Ответ: М = 157 Н∙м.

26. Определить момент инерции J тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на расстояние а = 20 см от одного из его концов.

Ответ: J = 4 10^-3 кгм².

27. Тонкий однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением ε = 3 с^-2 вокруг оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М. Во сколько раз изменится момент М, если ось вращения будет проходить через конец стержня?

Ответ: М = 25 мН∙м; n = 4.

28. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид φ = 4t² – t³. Найти закон изменения момента сил, действующих на шар, и значение момента сил через 2 с после начала вращения.

Ответ: М(t) = 1,28 – 0,96 t; М = – 0,64 Н∙м.

29. Охотник стреляет из ружья под углом  = 60^ к горизонту, находясь в лодке. Какую скорость приобретет лодка в момент выстрела, если средняя начальная скорость дроби υ = 320 м/с и её масса m = 35 г, масса охотника с лодкой М = 70 кг?

Ответ: υ_л = 0,08 м/с.

30. Снаряд, летевший со скоростью υ = 300 м/с, разорвался на два осколка. После взрыва больший осколок имел скорость υ₁ = 400 м/с, меньший – υ₂ = 100 м/с. Направление движения осколков не изменилось. Определить отношение масс осколков.

Ответ: m₁ / m₂ = 2.

31. На покоящейся тележке массой m₁ = 20 кг находится человек массой m₂ = 60 кг. Какую скорость υ₁ приобретёт тележка относительно земли, если человек пойдет по тележке со скоростью υ₂ = 3,6 км/ч относительно тележки?

Ответ: υ₁ = 0,75 м/с.

32. При поливе струя воды сечением S = 6 см² , движущаяся со скоростью υ = 12 м/с, упруго ударяется о стенку, расположенную перпендикулярно направлению движения струи, и отскакивает от неё без потери скорости. Найти изменение импульса струи, если время удара ∆t = 0,12 c .

Ответ: ∆Р = 20,7 кг∙м/с.

33. Найти момент инерции J и момент импульса L земного шара относительно оси вращения. Радиус Земли R = 6370 км, её масса m = 5,98∙10²⁴ кг, период вращения Т = 24 часа.

Ответ: J = 9,7∙10³⁷ кг∙м²; L = 7∙10³³ кг∙м²/с.

34. Горизонтальная платформа, имеющая форму диска, массой m₁ = 120 кг вращается с частотой n₁= 6 мин^-1. Человек массой m₂ = 80 кг стоит на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать, как для материальной точки.

Ответ: n₂ = 0,23 с^-1.

35. Маховик вращается согласно уравнению φ = 2 + 16t – 2t². Момент инерции маховика равен J = 50 кг∙м². Найти момент импульса маховика через 2 с после начала движения.

Ответ: L = 400 кг∙м²/ с.

36. Вентилятор начинает вращаться с постоянным угловым ускорением ε = 0,3 с^-2 и через 15 с после начала движения приобретает момент импульса L₁ = 30 кг∙м²/с. Найти кинетическую энергию вентилятора в этот момент времени.

Ответ:W_к = 67,5 Дж.

37. Стоящий на льду человек массой М = 60 кг ловит мяч массой m = 5 кг, летящий горизонтально со скоростью υ = 20 м/с. На какое расстояние откатится человек с мячом, если коэффициент трения  = 0,05?

Ответ: S = 2,4 м.

38. Для подъема зерна на высоту H = 10 м установили транспортер мощностью N = 4 кВт. Определить массу зерна, которую может поднять транспортер за 8 ч работы. Коэффициент полезного действия установки η = 13,6%.

Ответ: m = 157 т

39. Какую работу нужно совершить, чтобы поднять грунт на поверхность земли при рытье колодца, имеющего глубину h = 10 м и поперечное сечение S = 2 м²? Средняя плотность грунта  = 2 г/см³. Считать, что после подъёма грунт рассыпался тонким слоем на поверхности земли.

Ответ: А = 2 МДж.

40. Вагон массой m = 12 тонн двигался со скоростью υ = 3,6 км/ч. Налетев на пружинный буфер, вагон остановился, сжав пружину буфера на ∆х = 10 см. Найти жесткость пружины.

Ответ: k = 1,2 МН/м.

41. Однородный вертикально стоящий столб высотой h = 9 м падает на землю без проскальзывания. Какую угловую и линейную скорости будут иметь в конце падения верхний конец и середина столба?

Ответ:  = 1,8 рад/с, υ₁ = 16,2 м/с, υ₂ = 8,1 м/с.

42. Определить мощность электродвигателя, если его якорь вращается с частотой n = 1500 мин^-1, а момент силы М = 14 Н∙м.

Ответ: N = 2,2 кВт.

43. Определить линейную скорость υ шара, скатившегося без скольжения с наклонной плоскости высотой h = 1 м.

Ответ: υ = 3,77 м/с.

44. Маховик, момент инерции которого J = 40 кг∙м², начал вращаться равноускоренно из состояния покоя под действием момента силы М = 20 Н∙м. Вращение продолжалось в течение 10 с. Определить кинетическую энергию W_к, приобретенную маховиком.

Ответ: W_к = 500 Дж.

45. Определить массу молекулы аммиака NH₃.

Ответ: m =2,83∙10^–26 кг.

46. Сколько молекул содержится в кислороде массой m = 2 г?

Ответ: N = 3,75∙10²².

47. На изделие, площадь поверхности которого S = 20 см², нанесён слой серебра толщиной h = 1 мкм. Сколько атомов серебра N содержится в покрытии?

Ответ: N = 1,2∙10²⁰.

48. При никелировании изделия его покрывают слоем никеля толщиной h = 5 мкм. Сколько атомов никеля N содержится в покрытии, если площадь поверхности изделия S = 800 см²?

Ответ: N = 3,6·10²².

49. Сравните количество вещества, содержащееся в одинаковых объёмах ртути и алюминия.

Ответ: = 1,5.

50. Какова масса 20 моль серной кислоты?

Ответ: m = 1,96 кг.

51. Концентрация молекул межзвездного газа n в среднем равна 1 м^-3, средняя кинетическая энергия молекул газа ‹ › = 1,5∙10^-21 Дж. Определите давление Р межзвездного газа.

Ответ: Р = 10^-21 Па.

52. Чему равна концентрация n молекул воздуха в колбе радиолампы, если давление внутри колбы Р = 10^-5 Па, средняя кинетическая энергия молекул воздуха ‹› = 5∙10^-21 Дж?

Ответ: n = 3∙10¹⁵ м^-3.

53. Во сколько раз изменится давление Р неона в результате уменьшения его объёма V в 3 раза и увеличения средней кинетической энергии молекул ‹› в 2 раза?

Ответ: увеличится в 6 раз.

54. Определите среднюю кинетическую энергию молекул аргона ‹› и концентрацию молекул n при температуре t = 17 °С и давлении Р = 0,8 МПа.

Ответ: ‹› = 6∙10^-21 Дж; n = 2∙10²⁶ м^-3.

55. Известно, что основными компонентами сухого воздуха являются азот и кислород. Во сколько раз средняя арифметическая скорость молекулы азота отличается от средней арифметической скорости молекулы кислорода?

Ответ: в 1,07 раза.

56. Определить среднюю квадратичную скорость ‹υ_кв› молекул идеального газа при давлении Р = 10⁴ Па, если плотность газа  = 0,2 кг/м³ .

Ответ: ‹υ_кв› = 389 м/с.

57. При какой температуре Т средняя квадратичная скорость атомов гелия станет равной второй космической скорости υ = 11,2 км/с?

Ответ: Т = 20,1 кК.

58. При какой температуре наиболее вероятная скорость молекул водорода υ_в = 1,82 км/с?

Ответ: Т = 400 К.

59. Какова энергия вращательного движения молекулы кислорода при температуре t = –173 °С?

Ответ: ‹_вр› = 1,38∙10^-21 Дж.

60. Вычислить энергию вращательного движения всех молекул водяного пара массой m = 36 г при температуре t = 20 °С.

Ответ: W = 7,3 кДж.

61. Определить полную кинетическую энергию молекул водорода массой m = 4,4 г при температуре t = 27 °С.

Ответ: W = 13,7 кДж.

62. Найти полную кинетическую энергию молекул азота, содержащего количество вещества  = 1 кмоль при температуре t = 7 °C.

Ответ: W = 5,8 МДж.

63. Вычислить среднюю энергию поступательного движения молекул азота при температуре t = 137 °C.

Ответ: ‹_П› = 8,49∙10^-21 Дж.

64. В закрытом баллоне находится газ при нормальном атмосферном давлении и температуре t₁ = 27 °C. Определить давление газа, если его нагревают до температуры t₂ = 77 °С?

Ответ: р = 1,2∙10⁵ Па.

65. Для сварки израсходован кислород массой m = 3,2 кг. Найти минимальную ёмкость сосуда с кислородом, если стенки сосуда рассчитаны на давление p = 15,2 МПа. Температура газа в сосуде t = 17 °С.

Ответ: V = 15,9 л.

66. В баллон накачали водород, создав при температуре t = 6 °С давление р = 7,73 МПа. Определить плотность газа в баллоне.

Ответ:  = 7 кг/м³.

67. Для сварки был применен газ, находящийся в баллоне вместимостью V = 25 л при температуре t = 27 °С и давлении p₁ = 20,2 МПа. Определить массу израсходованного газа, если в баллоне установились давление газа р₂ = 4,04 МПа и температура t₂ = 23 °С. Относительная молекулярная масса газа M_r = 26.

Ответ: m = 4,1 кг.

68. Какой газ при давлении р = 0,808 МПа и температуре T = 240 К имеет плотность ρ = 0,81 кг/м³?

Ответ: водород.

69. Определить объём баллона, в котором находится кислород массой m = 4,3 кг под давлением p = 15,2 МПа при температуре t = 27 °С.

Ответ: V = 22 л.

70. Найти среднюю длину свободного пробега молекул водорода при температуре t = 27 °С и давлении р = 0,04 Па. Принять диаметр молекулы водорода d = 2,3·10^-8 см.

Ответ: ‹l› = 44 см.

71. Какова средняя частота соударений молекул воздуха при температуре t = 17 °С и давлении р = 101 кПа? Эффективный диаметр молекулы воздуха принять равным 0,35 нм.

Ответ: ‹z› = 6·10⁹ с^-1.

72. В баллоне с углекислым газом давление р = 5,06 МПа. При температуре t = 27°С среднее число соударений молекул ‹z› = 1,65·10¹¹ с^-1. Определить эффективный диаметр молекулы углекислого газа.

Ответ: d = 2,9·10^-8 см.

73. При каком давлении р средняя длина свободного пробега ‹l› молекул азота равна 1 м, если температура газа Т = 300 К?

Ответ: р = 6,5 мПа.

74. Определить градиент плотности углекислого газа в почве, если через её поверхность площадью S = 1 м² за время τ = 1 с в атмосферу прошёл газ массой m = 8·10^-8 кг. Коэффициент диффузии D = 0,04 см²/с.

Ответ: ∆/∆х = 0,02 кг/м⁴.

75. Вычислить массу газа, продиффундировавшего за время τ = 12 ч через поверхность почвы площадью S = 10 см², если коэффициент диффузии D = 0,05 см²/с. На глубине ∆x = 0,5 м плотность газа ρ₁ = l,2·10^-2 г/см³, а у поверхности - ρ₂ = 1,0·10^-2 г/см³.

Ответ: m = 0,086 кг.

76. В течение какого времени через поверхность почвы площадью S = 1 м² продиффундирует 480 мг углекислого газа, если коэффициент диффузии D = 0,05 см²/с при градиенте плотности ∆/∆х = 0,02 кг/ м⁴?

Ответ: t = 4800 c = 1,3 ч.

77. Найти коэффициент диффузии углекислого газа, если за 2 часа через поверхность почвы площадью S = 0,5 м² продиффундировал в атмосферу углекислый газ массой 720 мг при градиенте плотности ∆ρ/∆x = 0,04 кг/м⁴.

Ответ: D = 0,05 см²/с.

78. Определить толщину слоя суглинистой почвы, если за время τ = 5 ч через поверхность площадью S = 1 м² проходит количество теплоты Q = 250 кДж. Температура на поверхности почвы t₁ = 25 ^oC, в нижнем слое почвы температура t₂ = 15 °С.

Ответ: ∆x = 72 см.

79. Какое количество теплоты пройдет через песок, площадь поверхности которого S = 1 м², за время τ = 1 ч, если температура на его поверхности t₁ = 20 °С, а на глубине ∆x = 0,5 м температура t₂ = 10 °С?

Ответ: Q = 48 кДж.

80. Определить промежуток времени, в течение которого через кирпичную стену толщиной ∆x = 30 см и площадью S = 60 м² проходит количество теплоты Q = 150 кДж, если температура в помещении t₁ = 25 °С, а снаружи температура t₂ = 15 °С.

Ответ: t = 1,75 c.

81. Определить перепад температур ∆t между внешней и внутренней поверхностями бетонной стены, если через неё при толщине ∆x = 30 см и площади S = 10 м² за время t = 5 мин проходит количество теплоты Q = 100 кДж.

Ответ: ∆t = 10 ^oC.

82. Вычислить удельную теплоёмкость газа при постоянном давлении, если известно, что относительная молекулярная масса газа М_r = 30, отношение теплоемкостей C_P/C_V = I,4.

Ответ: с_р = 970 Дж/(кг∙К).

83. Во сколько раз показатель адиабаты для гелия больше, чем для кислорода?

Ответ: .

84. Вычислить удельные теплоёмкости водорода, гелия и кислорода при постоянном давлении.

Ответ: С_Н2 = 14540 Дж/(кг∙К); С_Не = 5194 Дж/(кг∙К);

С_О2 = 909 Дж/(кг∙К).

85. Найти удельные теплоёмкости азота и паров воды при постоянном объёме.

Ответ: С_N2 = 742 Дж/(кг∙К); С_H2O = 1385 Дж/(кг∙К).

86. Определить увеличение внутренней энергии паров ртути массой m = 200 г и их работу расширения при постоянном давлении, если температура возрастает на ∆Т = 100 К. Молекулы паров ртути одноатомные.

Ответ: ∆U = 1,25 кДж; А = 0,83 кДж.

87. Найти работу расширения водяного пара при постоянном давлении, если пару передано количество теплоты Q = 4 кДж.

Ответ: А = 1 кДж.

88. При изотермическом расширении водорода массой m = 1 г при температуре t = 7 °С его объём увеличился в три раза. Определить работу, совершенную водородом.

Ответ: А = 1,3 кДж.

89. Расширяясь, водород совершил работу А = 6 кДж. Определить количество теплоты Q, подведенное к газу, если процесс протекал: 1) изобарно; 2) изотермически.

Ответ: 1) Q= 21 кДж; 2) Q = 6 кДж.

90. При адиабатном расширении азота в количестве 2 моль его температура понизилась на ∆t = 20 °С. Какую работу совершил газ?

Ответ: А = 831 Дж.

91. Воздух, занимавший объём V₁ = 10 л при нормальном атмосферном давлении, был адиабатно сжат до объёма V₂ = 1 л. Найти давление газа после сжатия.

Ответ: р₂ = 2,5 МПа.

92. Определить работу адиабатного сжатия водорода массой m= 110 г, если в этом процессе температура газа повысилась на ∆T = 10 К.

Ответ: А = 1,14 кДж.

93. Объём паров ксенона при адиабатном сжатии уменьшился в два раза. Как изменилось давление?

Ответ: увеличилось в 3,25 раза.

94. Определить изменение энтропии ∆S азота массой m = 14 г при изотермическом увеличении объёма от V₁ = 2 л до V₂ = 6 л.

Ответ: ∆S = 4,55 Дж/К.

95. Найти изменение энтропии кислорода массой m = 4 кг при изохорном нагревании от температуры t₁ = 15 ^С до температуры t₂ = 100 ^С.

Ответ: ∆S = 675 Дж/К.

96. Кислород массой m = 2 кг увеличил свой объём в 5 раз: сначала –изотермически, затем – адиабатически. Найти изменение энтропии ∆S в каждом из указанных процессов.

Ответ: ∆S₁ = 836 Дж/К; ∆S₂ = 0 Дж/К.

97. Найти изменение энтропии ∆S при изобарном расширении азота массой m = 4 г от объёма V₁ = 5 л до объёма V₂ = 9 л.

Ответ: ∆S = 2,43 Дж/К.

98. Идеальный газ совершает цикл Карно, состоящий из двух изотерм

    Рис. 1

    (1-2, 3-4) и двух адиабат (2-3, 4-1) (рис. 1). Газ отдает охладителю 2/3 количества теплоты Q1, полученного от нагревателя. Температура охладителя T2 = 280 К. Определить температуру Т1 нагревателя. Ответ: Т1 = 420 К.

99. Идеальный газ совершает цикл Карно. Температура Т₁ нагревателя в три раза выше температуры Т₂ охладителя. Нагреватель передал газу количество теплоты Q₁ = 42 кДж. Какую работу А совершил газ?

Ответ: А = 28 кДж.

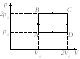
100. В цилиндре тепловой машины находится 1 моль идеального одно-

     Рис. 2

     атомного газа. Изменение состояния газа в цилиндре осуществляется по циклу, показанному на рис. 2. Определить термический кпд η тепловой машины. Ответ: η = 0,15.

101. Идеальный двухатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причём наибольшее давление газа в два раза больше наименьшего, а наибольший объём в четыре раза больше наименьшего. Построить график процесса в координатах р,V и p,T. Определить отношение работы А₁ газа при его изобарном расширении к работе газа А за весь цикл.

Ответ: А₁ /А = 2.

102. Каков средний диаметр капилляра почвы, если вода поднимается в капилляре на высоту h = 49 мм? Смачивание стенок считать полным.

Ответ: d = 0,6 мм.

103. Определить поверхностное натяжение касторового масла, если в трубке радиусом R = 0,5 мм оно поднялось на высоту h = 14 мм. Смачивание считать полным.

Ответ:  = 46 мН/м.

104. В стеклянной капиллярной трубке на Земле вода поднимается на 1 см. На какую высоту поднимется вода в той же трубке на Луне, где ускорение свободного падания равно 1,6 м/с²?

Ответ: h = 6,1 см.

105. Глицерин в капиллярной трубке диаметром d = 1 мм поднялся на высоту h = 20 мм. Определить коэффициент поверхностного натяжения глицерина. Смачивание считать полным.

Ответ:  = 63 мН/м.

106. Два шарика, расположенные на расстоянии d = 10 см друг от друга, имеющие равные по модулю, отрицательные заряды, взаимодействуют с силойF = 0,28 мН. Найти число "избыточных" электронов на каждом шарике.

Ответ: N =1,1·10¹¹.

107. На двух одинаковых капельках воды равной массы (m = 10 мг) находятся заряды по 10 нКл каждый. Во сколько раз сила электрического отталкивания капелек больше силы их взаимного гравитационного притяжения?

Ответ: n = 1,3·10¹⁴.

108. Два разноименных точечных заряда на расстоянии d = 9 см в вакууме притягиваются с такой же силой, как и в воде. Определить, на каком расстоянии располагаются заряды в воде. Диэлектрическая проницаемость воды = 81.

Ответ: r =0,01м.

109. Два точечных заряда q₁ = 10 нКл и q₂= –8 нКл расположены на расстоянииd =20 см друг от друга. Найти силу, действующую на зарядq = 2 нКл, расположенный посередине между зарядамиq₁и q₂.

Ответ: F = 32,4 мкН.

110. Заряды qи4qрасположены на расстоянииd друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий зарядq₁ так, чтобы система зарядов находилась в равновесии.

Ответ: х = 2/3 dот заряда 4q.

111. В вершинах квадрата находятся одинаковые по величине одноименные заряды q = 0,3 нКл.Определить величину зарядаq_о, который надо поместить в центр квадрата, чтобы система зарядов находилась в равновесии [5].

Ответ: q_о = –0,287 нКл.

112. Заряды q₁= –10 нКл иq₂ = –90 нКл расположены на расстоянииd= 4 см друг от друга. Где надо поместить третий отрицательный зарядq₃, чтобы он оказался в равновесии?

Ответ: На расстоянии 1см от зарядаq₁.

113. Три одинаковых заряда q= 1 нКл расположены в вершинах равностороннего треугольника. Какой отрицательный зарядq_онужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов?

Ответ: q_о= –0,578 нКл.

114. Два заряда q₁ = lнКл и q₂ = –3 нКл находятся на расстоянии d = 20 см друг от друга. Найти напряжённость и потенциал в точке поля, расположенной на продолжении линии, соединяющей заряды на расстоянииr₁ = 10cм от первого заряда.

Ответ: Е= 600 В/м; = 0 В.

115. Два заряда, один из которых по модулю в 4 раза больше другого, расположены на расстоянии d= 15 см друг от друга. На каком расстоянии от меньшего заряда напряжённость поля равна нулю, если заряды одноименные? Чему равен потенциал поля в этой точке, если меньший зарядq= 1 нКл?

Ответ: х=5 см;=540 В.

116. В точке, отстоящей от заряда qна расстоянииd = 30 см, напряжённость поляE = 2 кВ/м. Определить зарядqи потенциалφв этой точке поля.

Ответ: q = 20 нКл; = 600 В.

117. Два заряда q₁ = 4 нКл и q₂ = 4 нКл расположены на расстоянииd= 25см друг от друга. Найти напряжённость и потенциал в точке, находящейся на отрезке прямой, соединяющей заряды, на расстоянииr₁ = 5 см от первого заряда.

Ответ: E = 13,5к В/м;= 900 В.

118. Определить напряжённость электрического поля в мембране клетки толщиной d = 2·10^-5 мм, если на ней разность потенциаловU = 0,05 мкB. Поле мембраны считать однородным.

Ответ: E = 2,5 B/м.

119. Внутри горизонтально расположенного плоского конденсатора, расстояние между пластинами которого d= 4 мм, находится частица с зарядомq= 2 нКл. Для того, чтобы частица находилась в равновесии, между пластинами конденсатора нужно приложить разность потенциаловU =200 В. Найти массу частицы.

Ответ: m = 10мг.

120. Две бесконечные параллельные плоскости находятся на расстоянии d= 1 см друг от друга. На плоскостях равномерно распределены заряды с плотностями₁= 0,3 мкКл/м²и₂ = 0,5 мкКл/м². Найти разность потенциаловUмежду плоскостями.

Ответ: U= 113B.

121. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределённые по площади заряды с поверхностными плотностями ₁ = 2 нКл/м²и₂= –5 нКл/м². Определить напряжённостьЕполя между пластинами и вне пластин. Построить график изменения напряжённости вдоль линии, перпендикулярной пластинам.

Ответ: E₁ = 395,5 В/м;Е₂= 169,5B/м.

122. Вычислить потенциальную энергию W_псистемы двух точечных зарядовq₁= 100 нКл иq₂= 10 нКл, находящихся на расстоянииd = 10 см друг от друга.

Ответ: W_п = 90мкДж.

123. Найти потенциальную энергию W_псистемы трёх точечных зарядовq₁= 10 нКл,q₂= 20 нКл,q₃= –30 нКл, расположенных в вершинах равностороннего треугольника со сторонойа= 10 см.

Ответ: W_п=–63 мкДж.

124. Какова потенциальная энергия W_псистемы четырёх одинаковых точечных зарядовq= 10 нКл, расположенных в вершинах квадрата со сторонойа= 10 см?

Ответ: W = 48,7мкДж.

125. Определить потенциальную энергию W_псистемы четырёх точечных зарядов по 10 нКл каждый, расположенных в вершинах квадрата со сторонойа= 10 см, если два ближайших из них отрицательны.

Ответ: W_П = –12,8 мкДж.

126. Заряженная частица с начальной скоростью равной нулю, пройдя электрическое поле, приобрела скорость υ = 2 м/с. Какова разность потенциалов ускоряющего поля, если удельный заряд частицы (отношение заряда к массе)q/m= 40 мКл/кг?

Ответ:U = 50B.

127. Шарик массой m= 10^-4 кг, имеющий зарядq= 2·10^-4Кл, движется под действием сил однородного электрического поля. В точке, потенциал которойφ₁ = 0,5 кВ, шарик имел скорость₁= 10 м/c. Каков потенциал точки, в которой скорость шарика увеличится втрое?

Ответ: φ₂ = 300 B.

128. Между двумя пластинами, расположенными горизонтально в вакууме на расстоянии d = 5cм друг от друга, движется отрицательно заряженная шарообразная капелька воды массой m= 8·10^-6кг с ускорениема= 6 м/c, направленным вниз. Сколько "избыточных" электронов имеет капля, если разность потенциалов между пластинами U = 1 Кв?

Ответ: n= 95·10⁸.

129. По направлению силовой линии поля, созданного равномерно заряженной бесконечно протяженной плоскостью, в результате работы поля А= 50 Дж зарядq = 2 нКл переместился на расстояниеd= 2 см. Найти поверхностную плотность заряда на плоскости.

Ответ:  = 22,1 Кл/м².

130. Плоский воздушный конденсатор с площадью поверхности пластин S= 100 см² и расстоянием между нимиd = 2 мм заряжен до разности потенциаловU = 400 В. Найти энергию поля конденсатора.

Ответ: W= 3,54 мкДж.

131. Между пластинами плоского воздушного конденсатора находится плотно прилегающая к ним эбонитовая пластинка. Конденсатор заряжен до разности потенциалов U₁ = 60 В и отключён от источника тока. Какой будет разность потенциаловU₂, если из конденсатора удалить эбонитовую пластинку?

Ответ:U₂ = 180 В.

132. Плоский конденсатор, у которого расстояние между пластинами d= 0,5 см, заряжен до разности потенциаловU = 300 В. Определить объёмную плотность энергииw поля конденсатора, если диэлектрик – слюда.

Ответ: w = 0,11 Дж/м³.

133. Разность потенциалов на пластинах плоского воздушного конденсатора U= 300 В. Площадь каждой пластиныS= 100 см²и зарядq= 10 нКл. Определить расстояние между пластинами.

Ответ: d= 2,6 мм.

134. Через графитовый проводник в форме параллелепипеда длиной l = 30 см и площадью поперечного сечения S = 3 мм² течет ток I = 5 А. Найти разность потенциалов на концах графитового проводника.

Ответ: U= 1,95B.

135. Два элемента с одинаковыми эдс = 1,6 В и внутренними сопротивлениямиr₁ = 0_,2 Ом и r₂ = 0,8 Ом соединены параллельно и включены во внешнюю цепь, сопротивление которойR = 0,64 Ом. Найти силу тока в цепи.

Ответ: I = 2 A.

136. В цепь источника постоянного тока с эдс = 50 В и внутренним сопротивлениемr = 3 Ом включен резистор сопротивлениемR = 17 Ом. Определить напряжение на резисторе и силу тока, проходящего через него. Сопротивлением соединительных проводов пренебречь.

Ответ: U= 42,5B; I= 2,5A.

137. Какое добавочное сопротивление надо включить последовательно с лампочкой, рассчитанной на напряжение U₁ = 120 В и мощностьN= 60 Вт, чтобы она давала нормальный накал при напряженииU₂= 220 В? Сколько метров нихромовой проволоки сечениемS= 2·10^-3мм²понадобится для изготовление такого сопротивления?

Ответ: R= 200 Ом; l= 0,4 м.

138. Батарея, эдс которой  = 1,5 В, создаёт во внешней цепи токI = 1 А. Определить коэффициент полезного действия источника тока, если его внутреннее сопротивлениеr = 0,3 Ом.

Ответ:  =80%.

139. Определить мощность и силу тока, потребляемую электродвигателем, который приводит в действие насосную установку, поднимающую воду объёмом V = 3·10⁴ л на высоту h = 20 м. КПД установки η = 80%, напряжение в сети U = 220 В, двигатель работает 6 часов в сутки.

Ответ: I= 1,5A;N = 340Bт.

140. Коэффициент полезного действия источника тока, замкнутого на некоторое сопротивление, ₁ = 82 %. Каким будет КПД₂ , если заменить источник тока на два таких же, соединенных параллельно?

Ответ: ₂= 90%.

141. Чему равен коэффициент полезного действия источника при силе тока I= 0,8 А, если ток короткого замыканияI_кз = 2 А?

Ответ: = 60%.

142. Какой длины нужно взять никелиновую проволоку сечением S = 0,5 мм²для устройства кипятильника, в котором за времяΔt =15 минут можно вскипятить воду объёмомV = 1 л, взятую при температуреt = 10 °С? Напряжение в сетиU =110 В.КПД кипятильникаη = 60 %.

Ответ: l= 20,6 м.

143. Элемент с внутренним сопротивлением r= 4 Ом и эдс= 12 В замкнут проводником с сопротивлениемR= 8 Ом. Какое количество теплоты в единицу времени будет выделяться во внешней цепи?

Ответ: Q/t= 8 Дж/с.

144. На плитке мощностью N= 0,5 кВт стоит чайник, в который налит один литр воды при температуреt= 16 ºС. Вода в чайнике закипела через времяΔt= 20 минут после включения плитки. Найти КПД плитки.

Ответ:  = 58,8 %.

145. Какова должна быть площадь поперечного сечения никелиновой проволоки длиной l= 69 м, чтобы изготовить нагреватель, рассчитанный на напряжениеU= 220 В, при помощи которого можно нагреть воду объёмомV= 2 л от температурыt= 20º С до кипения за 10 минут при КПД= 80%?

Ответ: S= 0,84 мм².

146. Спай железоконстантановой термопары помещён в картофельный бурт, температура которого t= 80 ºC. Второй её спай находится в тающем льде. Стрелка гальванометра термопары отклонена наn = 40 делений, цена деления гальванометрас= 10^-6А/дел., постоянная термопарыk= 5 мкВ/ºС. Определить сопротивление гальванометра, если сопротивление проводов термопары пренебрежимо мало.

Ответ: r= 10 Ом.

147. Один спай термопары помещён в почву, температура которой t= 9,6 ºC, второй – погружён в тающий лёд. Определить постоянную термопары, если стрелка включённого в цепь термопары гальванометра с ценой деленияс= 1 мкА/дел. и сопротивлениемr = 12 Ом отклоняется на 40 делений. Сопротивлением термопары пренебречь.

Ответ: k = 50 мкВ/°С.

148. Один спай термопары помещён в печь, температура которой t = 480 ºC, другой – в тающий лед. Стрелка гальванометра, подключённого к термопаре, отклонилась при этом наn= 200 делений, сопротивление гальванометра вместе с термопаройr = 12 Ом. Постоянная термопарыk =5 мкВ/°С. Определить цену деления гальванометра.

Ответ: I = 1 мкА/дел.

149. Медьконстантановая термопара сопротивлением r₁ = 12 Ом присоединена к гальванометру сопротивлениемr₂ = 20 Ом. Один спай термопары находится при температуреt₁ = 22 °С, другой – помещён в стог сена. Сила тока в цепиI = 6,25 мкА. Постоянная термопарыk = 25 мкВ/°С. Определить температуру сена в стоге.

Ответ: t = 30 ºC.

150. Два длинных параллельных проводника находятся на расстоянии d = 5 см один от другого. По проводникам текут в противоположных направлениях одинаковые токи I₁ = I₂ = 10 А. Найти напряжённость Н магнитного поля в точке, находящейся на расстоянии r₁ = 2 см и r₂ = 3 см от соответствующих проводников.

Ответ: Н = 132 А/м.

150. Определить индукцию магнитного поля двух длинных прямых параллельных проводников с токами I₁ = 200 мА и I₂ = 400 мА одинакового направления в точке, лежащей на продолжении прямой, соединяющей проводники, на расстоянии r = 2 см от второго проводника. Расстояние между проводниками d = 10 см.

Ответ: В = 4,3 мкТл.

150. По двум длинным прямым параллельным проводникам в одном направлении текут токи I₁ = 1 А и I₂ = 3 А. Расстояние между проводниками d = 40 см. Найти индукцию магнитного поля в точке, находящейся посередине между проводниками.

Ответ: В = 2 мкТл.

150. По трём длинным прямым проводникам, расположенным в одной плоскости, параллельно друг другу, на расстоянии d = 3 см друг от друга текут токи силой I₁ = I₂ = 5 А и I₃ = I₁ + I₂. Определить индукцию магнитного поля, создаваемую токами в точке, находящейся посередине между первым и вторым проводниками.

Ответ: В = 44 мкТл.

150. В центре кругового витка с током радиусом R = 8 см напряжённость магнитного поля Н₀ = 0,3 А/см. Определить магнитный момент витка Р_m.

Ответ: Р_m = 0,1 А∙м².

150. По обмотке очень короткой катушки с числом витков N = 5 и радиусом R = 10 см течёт ток I = 2 А. Определить магнитный момент и индукцию магнитного поля в центре катушки.

Ответ: Р_m = 0,314 А∙м²; В₀ = 62,8 мкТл.

150. По двум круговым виткам радиусом 5 см, плоскости которых взаимно перпендикулярны, а центры совпадают, текут токи I₁ = I₂ =2 А. Найти индукцию результирующего магнитного поля в центре витков.

Ответ: В = 35 мкТл.

150. Найти разность потенциалов, которую надо приложить к концам витка диаметром d = 5 см, чтобы создать на его оси магнитное поле напряжённостью Н = 50 А/м. Сопротивление проводника R = 20 Ом.

Ответ: U = 0,5 В.

150. Прямой проводник длиной l = 10 см, по которому течёт ток I = 10 А, находится в однородном магнитном поле напряжённостью Н = 320 А/м. На проводник действует сила Ампера F_A = 200 мкН. Определить угол между вектором напряжённости Н и током в проводнике. Нарисовать рисунок.

Ответ:  = 30^.

150. На каком расстоянии друг от друга надо расположить два длинных параллельных проводника с токами I₁ = I₂ = 1 А, чтобы они взаимодействовали с силой F = 1,6 мкН на каждый метр длины? Нарисовать рисунок.

Ответ: r = 12,5 см.

150. По двум длинным прямым параллельным проводникам, находящимся на расстоянии r₁ = 20 см друг от друга, текут токи I₁ = 10 А и I₂ = 5 А. Определить силу взаимодействия токов, приходящуюся на 1 метр длины проводников. Как изменится эта сила, если проводники раздвинуть на расстояние r₂ = 30 см. При каком направлении токов проводники отталкиваются?

Ответ: F₁ = 50 мкН; F₁ / F₂ = 1,5.

150. Шины генератора представляют собой две параллельные медные полосы длиной l = 2 м каждая, отстоящие друг от друга на расстоянии d = 20 см. Определить силу взаимного отталкивания шин в случае короткого замыкания, когда по ним течёт ток I = 10 кА.

Ответ: F = 200 Н.

150. Электрон влетел в однородное магнитное поле, индукция которого В = 200 мкТл, перпендикулярно линиям индукции и описал дугу окружности радиусом R = 4 см. Определить кинетическую энергию электрона в эВ (1 эВ = 1,6∙10^-19 Дж).

Ответ: W_кин = 0,056 эВ.

150. Протон движется параллельно длинному прямому проводнику на расстоянии r = 2 мм от него. Какая сила действует на протон, если по проводнику течёт ток силой I = 10 А? Скорость протона υ = 3,4·10⁵ м/с.

Ответ: F_л = 5,4∙10^-17 Н.

150. Протон, влетая перпендикулярно горизонтальной составляющей магнитного поля Земли В_Г = 20 мкТл, движется по дуге окружности радиусом R = 10 см. Чему равны скорость протона в данной точке поля и период его вращения?

Ответ: υ = 192 м/с; Т = 3,3 мс.

150. Однозарядный ион массой m = 3,34∙10^-27 кг влетел перпендикулярно силовым линиям однородного магнитного поля с индукцией В = 400 мТл. Определить, на какую глубину в область поля может проникнуть протон, если его кинетическая энергия W_кин = 1 МэВ (1 эВ = 1,6∙10^-19 Дж).

Ответ: h = 50 см.

150. По обмотке электродвигателя, состоящей из 100 витков, течёт ток I = 10 А. Найти: магнитный момент обмотки, размеры которой 4 х 6 см²; максимальный вращающий момент сил, действующих на прямоугольную обмотку электродвигателя в магнитном поле индукцией В = 1200 мТл.

Ответ: М_max = 2,88 Н∙м, Р_m = 2,4 А∙м².

150. Проволочный виток радиусом R = 5 см находится в однородном магнитном поле напряжённостью Н = 2 кА/м. Плоскость витка составляет угол  = 60^ с направлением поля. По витку течет ток силой I = 4 А. Найти механический момент М, действующий на виток.

Ответ: М = 39,5 мкН∙м.

150. Проволочный виток радиусом R = 20 см расположен в плоскости магнитного меридиана. В центре витка установлен компас. Какой ток течет по витку, если магнитная стрелка компаса отклонена на угол  = 9^ от плоскости магнитного меридиана? Горизонтальная составляющая магнитного поля Земли В_Г = 20 мкТл.

Ответ: I = 1 А.

150. Короткая катушка площадью сечения S = 150 см², содержащая N = 10 витков, помещена в однородное магнитное поле напряжённостью Н = 80 А/см. Ось катушки составляет угол  = 60^ с силовыми линиями магнитного поля. Определить магнитный момент Р_m катушки и вращающий момент М, действующий на катушку, если по ней течёт ток I = 2 А.

Ответ: Р_m = 0,3 А∙м²; М = 260 мН∙м.

150. Соленоид содержит N = 1000 витков. Сила тока в обмотке I = 1 А, магнитный поток через поперечное сечение соленоида Ф = 0,1 мВб. Вычислить энергию магнитного поля [6].

Ответ: W = 50 мДж.

150. На стержень из немагнитного материала площадью сечения S = 100 см² и длиной l = 50 см намотан слой проводника так, что на каждый сантиметр его длины приходится n = 20 витков. Определить энергию и плотность энергии магнитного поля внутри соленоида, если сила тока в обмотке I = 5 А.

Ответ: W = 0,314 Дж; _э = 62,8 мкДж/см³.

150. Определить энергию магнитного поля короткой катушки, состоящей из N = 20 витков, если при силе тока I = 4 А в ней возникает магнитный поток Ф = 0,1 мВб.

Ответ: W = 4 Дж.

150. Обмотка электромагнита индуктивностью L = 0,5 Гн и сопротивлением R = 15 Ом находится под постоянным напряжением. Определить время t, в течение которого в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике электромагнита.

Ответ: t = 17 мс.

150. В однородном магнитном поле индукцией В = 40 мТл находится круговой виток радиусом R = 5 см, по которому течёт ток силой I = 1 А. Виток расположен так, что его плоскость перпендикулярна вектору магнитной индукции поля. Какую работу надо совершить, чтобы повернуть виток на 90^ вокруг оси, совпадающей с его диаметром?

Ответ: А = –314 мкДж.

150. Найти магнитный поток Ф, создаваемый соленоидом сечением S = 10 см², если он имеет n = 10 витков на каждый сантиметр длины при силе тока I = 20 А. Чему равно потокосцепление, если длина соленоида 15 см?

Ответ: Ф =25,1 мкВб;  =3,8 мВб.

150. В однородном магнитном поле индукцией В = 10 мТл находится прямой проводник длиной l = 8 см, расположенный перпендикулярно линиям индукции. По проводнику течёт ток I = 2 А . Под действием сил поля проводник переместился на расстояние d = 5 см. Найти работу сил поля.

Ответ: А = 80 мк Дж.

150. Плоский контур площадью S = 300 см² находится в однородном магнитном поле индукцией В₁ = 10 мТл. Плоскость контура перпендикулярна линиям индукции. В контуре поддерживается неизменный ток. При перемещении контура с током в область пространства, где индукция магнитного поля В₂ = 15 мТл, магнитное поле совершает работу А = 1,6 мДж. Найти величину тока в контуре.

Ответ: I = 10,7 А.

150. Магнитная индукция поля между полюсами двухполюсного генератора равна В = 800 мТл. Определить частоту n вращения якоря, если максимальное значение эдс индукции ε_max = 200 В. Ротор имеет N = 100 витков, площадь каждого витка S = 400см².

Ответ: n = 597 мин^-1.

150. Рамка площадью S = 200 см² равномерно вращается с частотой n = 10 с^-1 относительно оси, перпендикулярной линиям индукции магнитного поля (В = 200 мТл) и лежащей в плоскости рамки. Каково среднее значение эдс индукции <ε>, возникающей в рамке за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения?

Ответ: <ε> = 160 мВ.

150. Сила тока в соленоиде изменяется по закону I = 10t – t². Индуктивность соленоида L = 10 Гн. Найти значение эдс самоиндукции ε_с в соленоиде через 2 с после включения тока.

Ответ: ε_с = 60 В.

150. Найти значение эдс самоиндукции, возбуждаемой в обмотке электромагнита индуктивностью L = 400 мГн при равномерном изменении силы тока в ней на ∆I = 5 А за время ∆t = 0,02 с. Почему отключение мощных электродвигателей от питающей сети производят плавно и медленно с помощью реостатов?

Ответ: ε_с = 100 В.

150. Проволочное кольцо присоединёно к баллистическому гальванометру. Перпендикулярно плоскости кольца вдоль его оси ввели прямой магнит, при этом по цепи прошел заряд q =50 мкКл. Определить изменение магнитного потока ∆Ф через кольцо, если сопротивление цепи гальванометра R = 10 Ом. Изобразить контур и направление тока в нём.

Ответ: ∆Ф = 0,5 мВб.

150. Замкнутый проводник длиной l = 4 м (сложенный вдвое) разворачивают в квадрат в магнитном поле Земли. Вычислить наведённый в горизонтально расположенном контуре заряд, если известно, что сопротивление проводника R = 500 мОм. Вертикальная составляющая вектора магнитной индукции поля Земли В = 50 мкТл. Изобразить контур и направление тока в нём.

Ответ: q = 0,1 мКл.

150. Заряд q = 400 мКл проходит по витку при уменьшении магнитного потока внутри витка на ∆Ф = 12 мВб. Найти сопротивление проводника, из которого выполнен виток. Изобразить контур и направление тока в нём.

Ответ: R = 30 мОм.

150. Проволочное кольцо диаметром d = 20 см лежит на столе. Какое количество электричества q пройдет по кольцу, если его повернуть с одной стороны на другую? Сопротивление кольца R = 1 Ом. Вертикальная составляющая индукции магнитного поля Земли В = 50 мкТл. Изобразить контур и направление тока в нём.

Ответ: q = 3,14 мкКл.

150. Точка совершает колебания по закону x = 0,05sin2t (м). Построить графики зависимости от времени: 1) смещения х(t); 2) скорости (t); 3) ускорения а(t). Определить ускорение a через время t = 1/3 c после начала колебаний.

Ответ: а = –1,7 м/с².

150. Тело совершает гармонические колебания. Период колебаний Т = 0,15 с, максимальная скорость _max = 8 м/с. Определить амплитуду колебаний A. Построить график зависимости смещения от времени, считая, что в момент времени t = 0 смещение х(t) = 0.

Ответ: А = 19 cм.

150. Максимальная скорость колебаний точки _max = 1 м/с, амплитуда колебаний А = 2 мм. Определить максимальное ускорение точки a_max. Построить график зависимости скорости от времени при условии, что в момент времени t = 0 смещение х(t) = 0.

Ответ: а_max = 500 м/с².

150. Максимальное ускорение колеблющегося тела а_max = 10³ м/с², амплитуда колебаний А = 10 см. Определить частоту колебаний тела v. Построить график зависимости ускорения от времени, если начальная фаза колебаний φ₀ = 0.

Ответ: v = 15,9 Гц.

150. Тело совершает гармонические колебания по закону 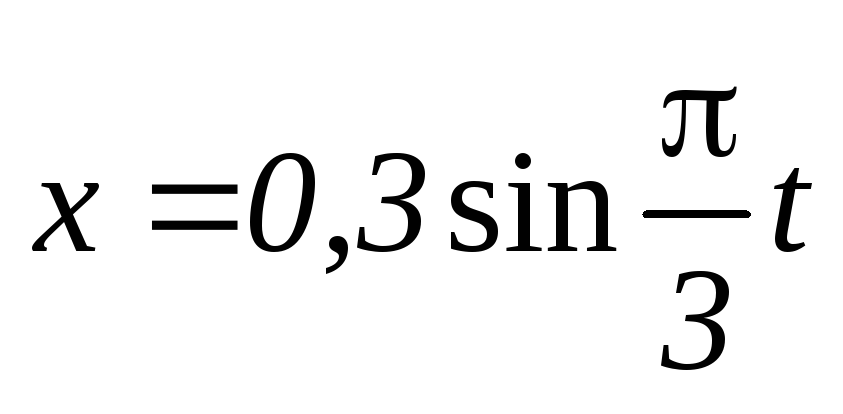(м). Определить амплитуду возвращающей силыF_max, если масса тела m = 2 кг. Построить график зависимости силы F от времени t.

Ответ: F_max = 657 мН.

150. Тело совершает гармонические колебания по закону 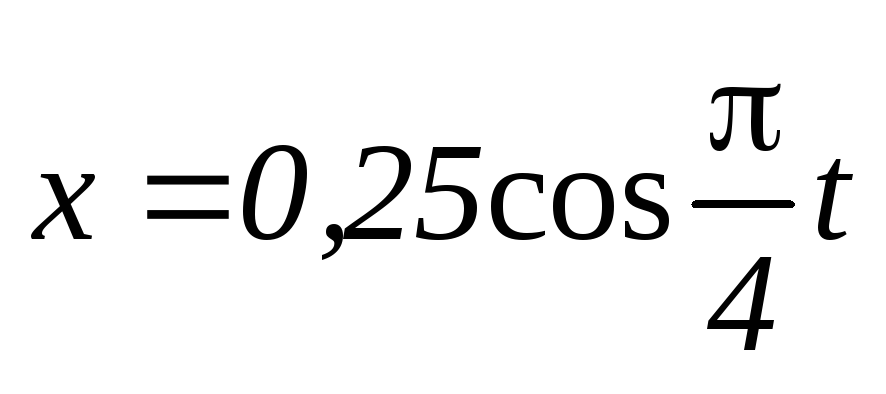(м). Определить полную энергию телаW, если его масса m = 1,4 кг. Построить графики зависимости от времени потенциальной W_п , кинетической W_к и полной W энергий колебаний.

Ответ: W = 27 мДж.

150. Колебания материальной точки m = 10 г происходят согласно уравнению х = Аcosωt, где А = 5 см; ω = 20 с^-1. Определить максимальное значение кинетической энергии W_k. Построить графики зависимости от времени потенциальной W_п, кинетической W_к и полной W энергий колебаний точки.

Ответ: W_к = 5 мДж.

150. Материальная точка массой m = 50 г колеблется согласно уравнению х = Асоsωt, где А = 10 см, ω = 5 рад/с. Найти силу F, действующую на точку, в двух случаях: 1) в момент, когда фаза ωt = π/3; 2) в положении наибольшего смещения точки.

Ответ: F₁ = 62,5 мН; F₂ = 125 мН.

150. На какую часть нужно уменьшить длину L математического маятника, чтобы период его колебаний на высоте Н = R_Земли был равен периоду его колебаний на поверхности Земли?

Ответ: на 3/4 L .

150. Груз массой m = 8 кг, подвешенный на пружине, совершает гармонические колебания с периодом Т. Груз какой массы нужно снять, чтобы период колебаний уменьшился в два раза?

Ответ: Δm = 6 кг.

150. За одно и то же время один математический маятник делает 50 колебаний, а другой 30. Найти их длины, если один из них на 32 см короче другого.

Ответ: l₁ = 0,18 м; l₂ = 0,5 м.

150. Определить период колебаний математического маятника на Луне, если на Земле его период Т = 5 с.

Ответ: Т_л =12,4 с.

150. Ареометр массой m = 0,2 кг плавает в жидкости. Если его погрузить немного в жидкость, а затем отпустить, то он начнет совершать колебания с периодом Т = 3,4 с. Считая колебания ареометра гармоническими и незатухающими, найти плотность жидкости , в которой он плавает. Радиус вертикальной цилиндрической трубки ареометра R = 5 мм.

Ответ:  = 869 кг/м³.

150. Поплавок совершает малые вертикальные гармонические колебания в воде с частотой ν = 1 с^-1. Пренебрегая сопротивлением воды, найти массу поплавка. Площадь поперечного сечения поплавка S = 0,25 см².

Ответ: m = 6,3 г.

150. Бревно из берёзы, сечение которого постоянно по всей длине, погрузилось вертикально в воду так, что над водой находится лишь малая по сравнению с длиной его часть. Период колебания бревна Т = 13 с. Определить длину L бревна.

Ответ: L = 3,0 м.

150. Ареометр массой m = 50 г, имеющий трубку диаметром d = 1 см, плавает в воде. Его немного погрузили в воду и затем предоставили самому себе, в результате чего ареометр стал совершать гармонические колебания. Найти период Т этих колебаний.

Ответ: Т = 1,6 с.

150. Найти смещение точки, удалённой от источника колебаний на расстояние l = /12, для момента времени t = T/6. Амплитуда колебаний А = 5 см.

Ответ:  = 0,04 м.

150. Смещение точки, находящейся на расстоянии 4 см от источника колебаний, в момент t = T/3 равно половине амплитуды. Найти длину бегущей волны.

Ответ:  = 24 см.

150. Распространяющаяся в упругой среде плоская звуковая волна имеет период Т = 3 мс, амплитуду А = 0,2 мм и длину волны  = 1,2 м. Для точек среды, удалённых от источника колебаний на расстояние х = 2 м, найти смещение в момент времени t = 7 мс.

Ответ:  = –0,1 мм.

150. От источника колебаний распространяется волна вдоль прямой линии. Амплитуда колебаний А = 10 см. Найти в момент времени t = 0,9Т смещение точки, удалённой от источника на расстоянии х = 3/4.

Ответ:  = 5,9 см.

150. Электромагнитные волны частотой  = 1 МГц распространяются в однородной среде со скоростью  = 2·10⁸ м/с. Каковы длины этих волн λ₀ и λ в вакууме и среде соответственно?

Ответ: ₀ = 300 м; λ = 200 м.

150. Сравните длины звуковых волн частотой  = 0,44 кГц в воздухе и в воде, если скорость звука в воздухе ₁ = 330 м/с, а в воде ₂ = 1,5 км/с.

Ответ: ₂ /₁ = 4,55.

150. Звуковая волна частотой  = 1,25 кГц распространяется в металле. Между двумя точками, находящимися на расстоянии l = 2 м, разность фаз колебаний Δ = . Чему равна скорость звука в металле?

Ответ:  = 5 км/с.

150. Сдвиг по фазе напряжения в начале и в конце линии электропередачи 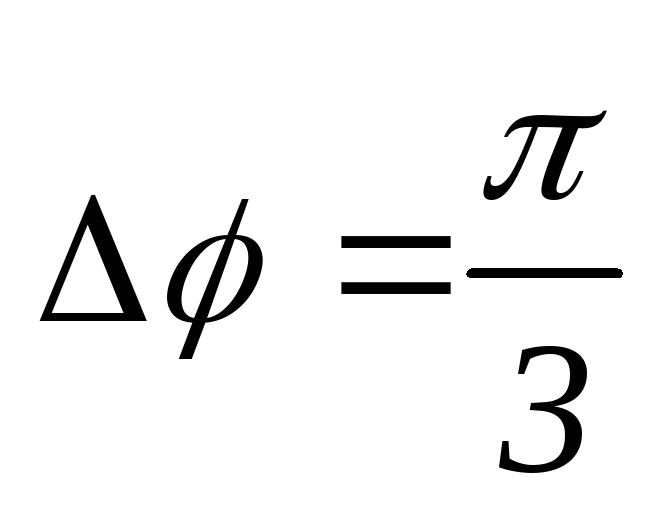. Найти длину этой линии, если частота изменения напряжения = 50 Гц.

Ответ: L = 1000 км.

150. Определить разность фаз колебаний двух точек, отстоящих друг от друга на расстояние L = 20 см, если волна распространяется со скоростью  = 2,4 м/с и частотой  = 3 Гц.

Ответ: Δ = 1,57 рад.

150. Скорость звука в воде  = 1450 м/с. На каком расстоянии находятся две ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний  = 725 Гц?

Ответ: ∆r = 1 м.

150. Две точки находятся на расстоянии Δх = 50 см друг от друга на прямой, вдоль которой распространяется волна со скоростью υ = 50 м/с и периодом колебаний Т = 0,05 с. Найти разность фаз Δφ колебаний этих точек.

Ответ: ∆φ = 2 рад.

150. На озере в безветренную погоду с лодки бросили тяжёлый якорь. От места бросания пошли волны. Человек, стоящий на берегу, заметил, что волна дошла до него через время t = 50 с, расстояние между соседними горбами волн 0,5 м, а за время τ = 5 с было 20 всплесков о берег. Как далеко от берега находилась лодка?

Ответ: S = 100 м.

150. Какую электроёмкость должен иметь конденсатор для того, чтобы колебательный контур радиоприёмника, состоящий из этого конденсатора и катушки индуктивностью L = 10 мГн, был настроен на волну  = 1 км?

Ответ: C = 28 пФ.

150. Колебательный контур состоит из конденсатора электроёмкостью С = 0,01 мкФ и катушки индуктивностью L = 0,01 мГн. На какую длину волну настроен контур?

Ответ:  = 595 м.

150. Резонансная частота колебательного контура ν₁ = 50 МГц. Как нужно изменить расстояние между пластинами плоского конденсатора в контуре, чтобы резонансная частота стала ν₂ = 70 МГц?

Ответ: увеличить в 1,96 раза.

150. Во сколько раз уменьшится период свободных колебаний в колебательном контуре, если конденсатор контура заменить на два таких же последовательно соединённых конденсатора?

Ответ: n = 1,41.

150. Мальчик несёт на коромысле вёдра с водой, период собственных колебаний которых T = 1,5 с. При какой скорости υ движения мальчика вода начнёт особенно сильно выплёскиваться, если длина шага мальчика равна l = 60 см?

Ответ: υ =0,4 м/с.

150. Вагон массой m = 80 т имеет рессоры, жёсткость которых k = 500 кН/м. При какой скорости υ вагон начнёт сильно раскачиваться вследствие толчков на стыках рельов, если длина рельса L =12,8 м?

Ответ: υ = 18 км/ч.

150. В вагоне поезда подвешен маятник длиной l =1 м. При движении поезда маятник особенно сильно раскачивается от толчков на стыках рельсов при скорости поезда υ = 45 км/ч. Какова длина рельсов L?

Ответ: L = 25 м.

150. Девочка идёт со скоростью υ = 0,45 м/с и несёт на коромысле вёдра с водой, которая сильно выплёскивается. Найти длину шага l девочки, если период колебаний вёдер Т = 1,2 с.

Ответ: l = 54 см.

150. На гладком горизонтальном столе лежит шар массой М = 220 г, прикрепленный к пружине жёсткостью k = 30 кН/м. В шар попадает пуля массой m = 10 г. Определить скорость пули, направленную вдоль оси пружины, в момент удара, если амплитуда колебаний шара А = 5 см. Удар считать абсолютно неупругим, сопротивлением воздуха и массой пружины пренебречь.

Ответ: υ = 415 м/с.

150. На горизонтальном абсолютно гладком столе лежит тело массой М = 10 кг, прикреплённое к стене с помощью пружины. В это тело попадает и застревает в нём пуля массой m = 10 г, летящая со скоростью υ = 500 м /с, направленной вдоль оси пружины. Тело с пулей отклоняется от положения равновесия и совершает колебания с амплитудой А = 10 см. Определить коэффициент жёсткости пружины k. Массой пружины и сопротивлением воздуха пренебречь.

Ответ: k = 250 Н/м.

150. Упругая пружина жесткостью k = 40 Н/м подвешена вертикально, к её нижнему концу подвесили тело массой m = 0,8 кг. В некоторый момент тело оттянули вниз на расстояние х = 0,15 м и освободили. Определить период колебаний и максимальную высоту подъёма тела.

Ответ: Т = 0,9 с; х_max = 0,15 м.

150. На горизонтальной поверхности лежит шарик массой m, прикреплённый к стене с помощью пружины, жёсткость которой равна k. Шарик сместили из положения равновесия на расстояние x_о и толкнули его к положению равновесия, сообщив ему начальную скорость υ_о. Найти амплитуду колебаний А. Массой пружины и трением пренебречь.

Ответ: .

150. Увеличение микроскопа Г = 600. Определить оптическую силу D объектива, если фокусное расстояние окуляра F₂ = 4 см, длина тубуса L = 24 см.

Ответ: D = 5 дптр.

150. Фокусные расстояния объектива и окуляра микроскопа соответственно равны F₁ = 3 мм, F₂ = 3 см. Предмет находится на расстоянии a = 3,1 мм от объектива. Вычислить увеличение объектива, окуляра и микроскопа.

Ответ: Г₁ = 30; Г₂ = 8,3; Г = 249.

150. Фокусное расстояние объектива микроскопа F₁ = 4 мм, окуляра F₂ = 5 см. Найти увеличение Г этого микроскопа, если предмет помещен на расстоянии а = 4,2 мм от объектива микроскопа.

Ответ: Г = 105.

150. Фокусное расстояние объектива микроскопа F₁ = 2 мм, окуляра – F₂ = 5 мм. Расстояние между объективом и окуляром равно 20 см. Каково увеличение микроскопа для наблюдателя, расстояние наилучшего зрения у которого L = 20 см? Какого увеличение Г_Н микроскопа для нормального глаза?

Ответ: Г = 3900; Г_Н = 4875.

150. Оптимальное значение освещенности, необходимое для ускорения роста черенков черной смородины, E = 800 лк. На какой высоте h помещен источник света силой I = 200 кд? Свет падает перпендикулярно поверхности грядки.

Ответ: h = 50 см.

150. В теплице для выращивания рассады огурцов подвешена лампа, создающая на почве освещённость E = 100 лк. Определить силу света I лампы, если свет падает нормально к поверхности почвы (расстояние от лампы до почвы h = 0,6 м) .

Ответ: I = 36 кд.

150. При выращивании ранней капусты выбирается площадка квадратной формы со стороной 1,3 м. Лампа силой света I = 400 кд подвешена над центром площадки на высоте h = 2,2 м. Определить максимальную E_max и минимальную E_min освещённости площадки.

Ответ: E_max = 82,8 лк; E_min = 62,5 лк.

150. Норма минимальной освещённости для содержания птиц E = 60 лк. Определить силу света лампы, которую необходимо подвесить на высоте h = 2 м, чтобы создать под ней такую освещённость.

Ответ: I = 240 кд.

150. Две когерентные волны приходят в некоторую точку пространства с оптической разностью Δ = 2,25 мкм. Каков результат интерференции в этой точке, если свет: красный (_кр = 750 нм); зеленый (_з = 500 нм)?

Ответ: а) усиление; б) ослабление.

150. Световые волны длиной волны  = 600 нм интерферируют. Геометрическая разность хода лучей ∆х = 1,2 мкм. Что наблюдается вследствие интерференции, если световые волны распространяются: а) в воздухе; б) в воде; в) в скипидаре?

Ответ: В первом и третьем случаях наблюдается

усиление света, во втором - его ослабление.

150. Во сколько раз изменится расстояние между интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (_з = 500 нм) заменить красным (_кр = 650 нм)?

Ответ: увеличится в 1,3 раза.

150. В опыте Юнга расстояние между щелями d = 1 мм, расстояние от щелей до экрана L = 3 м. Найти положение двух первых светлых полос, если длина световых волн λ = 600 нм.

Ответ: х₁ = 1,8 мм; х₂ = 3,6 мм.

150. На дифракционную решётку нормально падает свет с длиной волны  = 0,6 мкм. Третий дифракционный максимум виден под углом  = 2°. Определить постоянную решётки.

Ответ: d = 0,05 мм.

150. Определить число штрихов на 1 мм дифракционной решётки, если свет с длиной волны  = 600 нм нормально падает на решётку и даёт первый дифракционный максимум на расстоянии l = 3,3 см от центрального. Расстояние от решётки до экрана L = 110 см.

Ответ: 50 штрихов на 1 мм.

150. На дифракционную решётку с периодом d = 10 мкм нормально падает белый свет. Найти ширину Δl спектра первого порядка, полученного на экране, если расстояние от решётки до экрана L = 1,5 м. Границы видимого диапазона: _ф = 400 нм и _кр = 780 нм.

Ответ:∆l = 5,7 см.

150. Дифракционная решётка, имеющая 50 штрихов на 1 мм, расположена на расстоянии L = 55 см от экрана. Какова длина волны монохроматического света, падающего нормально на решётку, если первый дифракционный максимум на экране отстоит от центрального на расстоянии l = 1,9 см?

Ответ:  = 690 нм.

150. Определить удельное вращение [α] раствора сахарозы в соке сахарного тростника, если угол поворота плоскости поляризации  =17° при длине трубки с раствором l = 10 см. Концентрация раствора С = 0,25 г/см³.

Ответ: [α]= 0,68 град/(м·%).

150. При прохождении света через слой 10%-го сахарного раствора толщиной l₁ = 15 см плоскость поляризации света повернулась на угол ₁ = 12,9°. В другом растворе в слое толщиной l₂ = 12 см плоскость поляризации повернулась на угол ₂ = 7,2°. Найти концентрацию С₂ второго раствора

Ответ: С₂ = 7 %.

150. При прохождении через трубку длиной l = 20 см с сахарным раствором плоскость поляризации света поворачивается на угол  = 5°. Удельное вращение раствора сахара [α]= 0,6 град/(м· %). Определить концентрацию раствора.

Ответ: С = 42 %.

150. Определить удельное вращение раствора сахарозы, если угол поворота плоскости поляризации  = 8,5° при длине трубки с раствором l = 2 дм. Концентрация раствора С = 0,25 г/см³.

Ответ: [α]= 0,17 град/(м·%).

150. При какой температуре излучательность (энергетическая светимость) почвы R = 256 Вт/м²? Считать почву чёрным телом.

Ответ: t = –14 С.

150. Вычислить энергию, излучаемую с поверхности площадью S = 1 м² пахотного поля при температуре почвы t = 27 ^С за время τ = 1 мин.

Ответ: W = 27,6 кДж.

150. Принимая, что Солнце излучает как абсолютно черное тело, определить температуру его поверхности, если длина волны, на которую приходится максимум энергии излучения,  =0,5 мкм.

Ответ: Т = 5800 К.

150. Максимум энергии излучения песчаной почвы приходится на длину волны λ₁ = 10 мкм. На какую длину волны λ₂ сместится максимум, если температура почвы понизится на ∆Т = 90 К?

Ответ: ₂ = 14,5 мкм.

150. Работа выхода электронов из натрия А = 2,27 эВ. Найти красную границу фотоэффекта для натрия.

Ответ: _кр = 548 нм.

150. На металл падает свет длиной волны  = 437 нм. Определить максимальную скорость фотоэлектронов. Работой выхода пренебречь.

Ответ:  = 1000 км/с.

150. Вычислить кинетическую энергию фотоэлектрона, вылетевшего из натрия при облучении его светом длиной волны  = 200 нм. Работа выхода электрона из натрия A = 2,27 эВ.

Ответ: Т = 4 эВ.

150. Произойдёт ли фотоэффект при освещении металла светом длиной волны  = 500 нм? Работа выхода электрона из металла А = 2 эВ.

Ответ: Произойдёт.

150. Какую энергию следует сообщить атому водорода, чтобы перевести электрон со второго энергетического уровня на шестой?

Ответ:  = 3 эВ.

150. Электрон в атоме водорода перешёл с четвертого энергетического уровня на второй. Определить длину волны испускаемого фотона[7].

Ответ:  = 488 нм.

150. Вычислить энергию, которую поглощает атом водород при переходе электрона со второго энергетического уровня на пятый.

Ответ:  = 2,86 эВ.

150. Какова частота электромагнитной волны, излучаемой атомом водорода, при переходе электрона с четвёртого энергетического уровня на третий?

Ответ:  = 1,6∙10¹⁴ Гц.

150. Свет, падая на зеркальную поверхность, оказывает давление ρ = 10 мкПа. Определить энергию света, падающего на поверхность площадью S = 1 м² за время ∆t = 1 с.

Ответ: W = 1,5 кДж.

150. Вычислить давление солнечных лучей, падающих нормально на чернозем. Солнечная постоянная С = 1,39 кДж/(м²·с). Коэффициент отражения чернозема ρ = 0,08.

Ответ: р = 4,7 мкПа.

150. Вычислить давление солнечных лучей, падающих нормально на песчаную почву, коэффициент отражения которой ρ = 0,6. Солнечная постоянная С = 1,39 кДж/(м²·с).

Ответ: р = 7,4 мкПа.

150. Параллельный пучок лучей падает нормально на почву, мульчированную молотым мелом, и производит давление р = 5,4 мкПа. Коэффициент отражения мела ρ = 0,8. Определить энергию излучения, падающего за время ∆t = 1 с на площадь S = 1 м².

Ответ: W = 900 Дж.

150. Найти длину волны де Бройля  молекул водорода, движущихся с наиболее вероятной скоростью _в в газе при температуре t = 0 ^C.

Ответ:  = 1,33 Å.

150. При увеличении энергии электрона на ∆W = 200 эВ его длина волны де Бройля уменьшится в 2 раза. Найти первоначальную длину волны де Бройля электрона.

Ответ:  = 1,5 Å.

150. Электроны разогнали в электрическом поле при напряжении U = 30 В. Найти длину волны де Бройля этих электронов.

Ответ:  = 2,2 Å.

150. При каком значении кинетической энергии протона длина волны де Бройля  = 1 Å?

Ответ:  = 0,083 эВ.

150. На животноводческой ферме для дезинфекции воздуха в помещении молодняка провели ультрафиолетовое облучение. Интенсивность облучения J = 6 Вт/м², длина волны  = 254 нм. Сколько фотонов пролетело через поверхность площадью S = 1 м² за время ∆t = 1 с? Поверхность перпендикулярна лучам.

Ответ: N = 7,7∙10¹⁸ фотонов.

150. На растительные клетки воздействуют ультрафиолетовым излучением длиной волны  = 254 нм. Определить частоту и энергию фотона этого излучения.

Ответ:  = 1,2∙10¹⁵ Гц;  = 5 эВ.

150. Лазерной установкой в течение 10 мин облучаются семена огурцов. Длина волны излучаемого света  = 632 нм, интенсивность излучения J = 250 Вт/м². Сколько фотонов поглощено семенем площадью S = 4 мм²?

Ответ: N = 1,9∙10²⁸ фотонов.

150. Определить энергию , массу m и импульс р фотона, которому соответствует длина волны λ = 380 нм (фиолетовая граница видимого спектра).

Ответ:  = 3,27 эВ; m = 5,8∙10^-36 кг; р = 1,74∙10^-27 кг∙м/с.

150. В организме человека содержание калия составляет примерно 0,15% от его массы. Радиоактивный изотоп в природной смеси изотопов составляет 0,012%, период полураспада изотопаТ_1/2 = 1,24 млрд. лет. Сколько ядер изотопа калия распадается за времяt = 1 с в тканях организма человека массой m = 60 кг?

Ответ: А = 2,9∙10⁴ Бк.

150. Для агробиологических исследований в питательную смесь введён радиоактивный изотоп 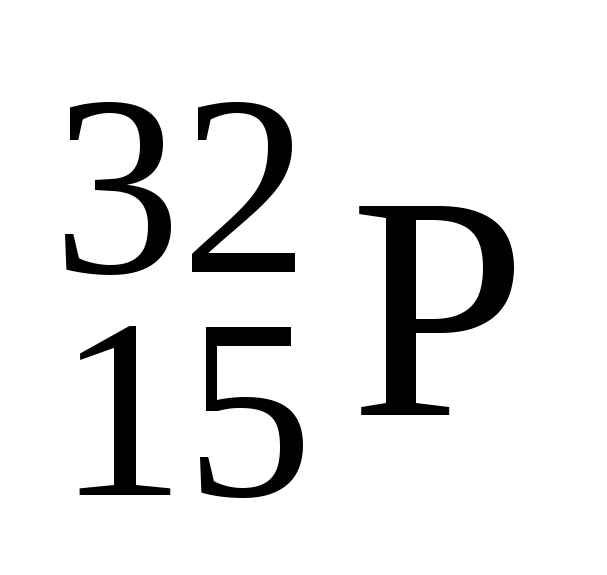массойm = 1 мг, период полураспада которого равен Т_1/2 = 14,28 сут. Определить постоянную распада λ и активность фосфора А.

Ответ:  = 5,6∙10^-7 с^-1; А = 10¹³ Бк.

150. При радиометрических исследованиях в навеске почвы обнаружен стронций 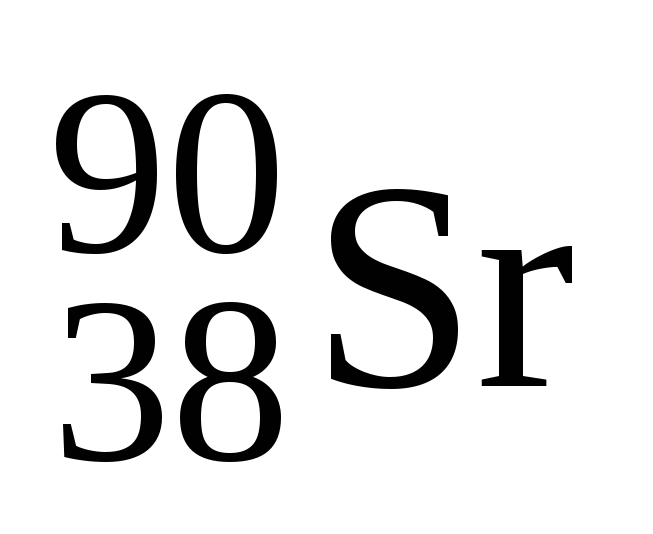, активность которогоА =10⁷ Бк. Какова масса стронция в навеске? Период полураспада T_1/2= 27,7 года.

Ответ: m = 1,9 нкг.

150. Для семян пшеницы, замоченных в растворе азотнокислого натрия, содержащем радиоактивный изотоп 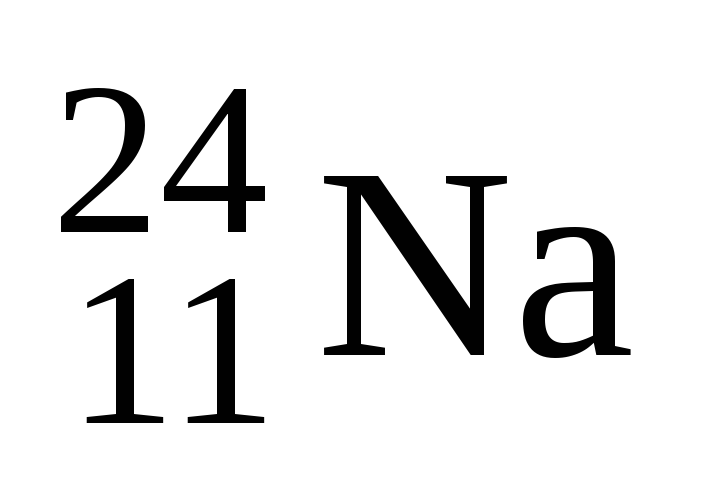, активностьА = 22,310^-6 Бк. Какова масса поглощённого зернами радиоактивного изотопа? Период полураспада изотопа T_1/2 = 14,96 дня.

Ответ: m = 1,65∙10^-24 кг.

150. Вычислить дефект массы ∆m и энергию связи ядра дейтерия E_св .

Ответ: ∆m = 0,0024 а.е.м.; Е_св = 2,23 МэВ.

150. Найти удельную энергию связи Е_уd, т.е. энергию связи, приходящуюся на один нуклон ядра изотопа углерода .

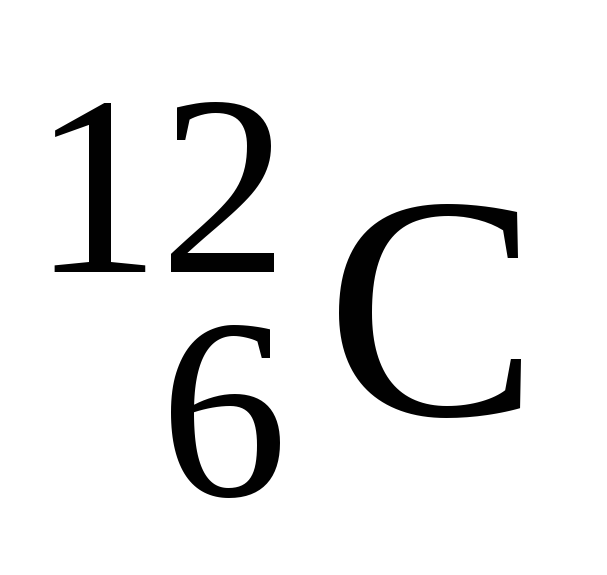Ответ: Е_уд = 7,68 МэВ/нуклон.

150. Определить дефект массы ∆m и энергию связи Е_св ядра трития .

Ответ: ∆m = 0,00912 а.е.м.; Е_св = 8,4 МэВ.

150. Вычислить удельную энергию связи Е_уд, т.е. энергию связи, приходящуюся на один нуклон ядра изотопа гелия .

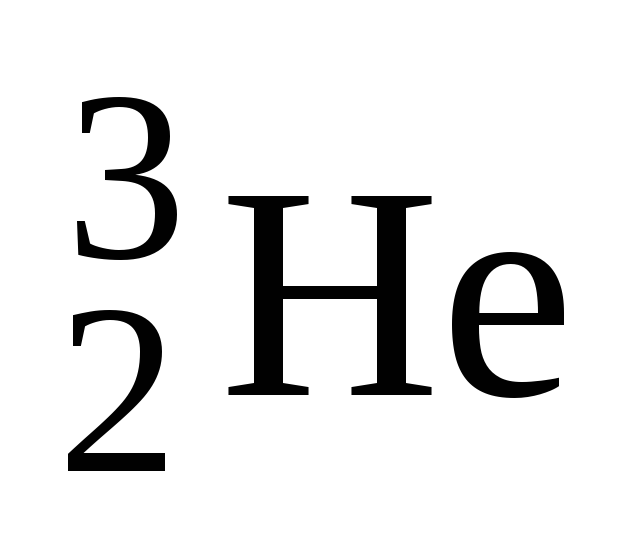Ответ: Е_уд = 2,58 МэВ/нуклон.

150. Вычислить энергию ядерной реакции 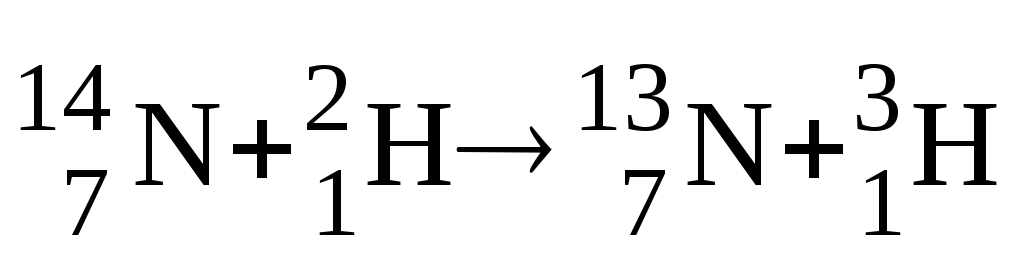.Выделяется или поглощается эта энергия?

Ответ: энергия поглощается; Q = 4,3 МэВ.

150. Определить энергию ядерной реакции 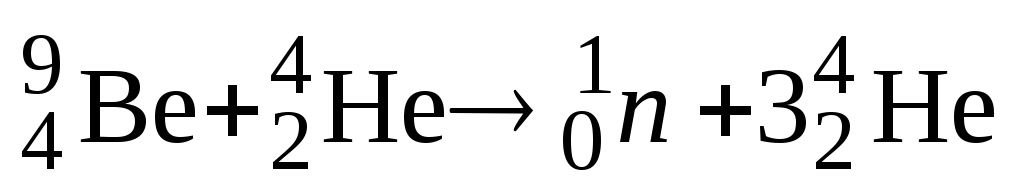. Выделяется или поглощается энергия?

Ответ: энергия поглощается; Q = 1,56 МэВ.

150. Какое количество энергии выделяется при ядерной реакции ?

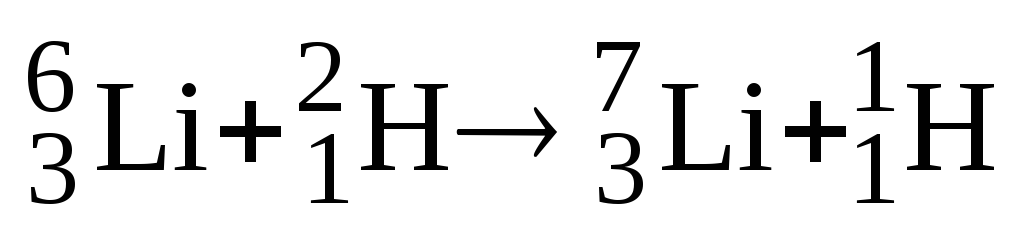Ответ:Q = 5,02 МэВ.

150. Вычислить энергию термоядерной реакции .

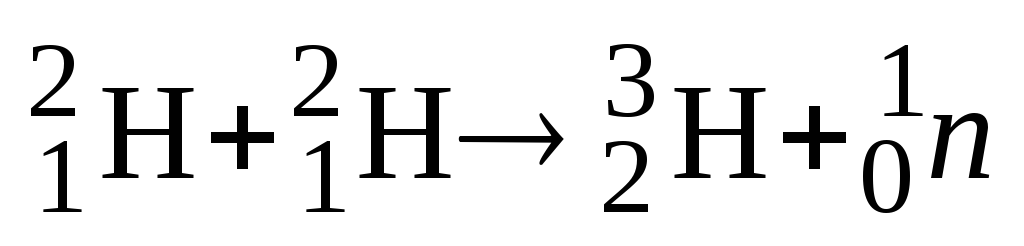Ответ: Q = 3,26 МэВ.