
- •Часть 1. Гидравлика
- •Основные понятия и законы
- •Жидкости и их свойства
- •1.2. Скоростное поле среды в окрестности точки
- •1.3. Силы, действующие в жидкости
- •1.4. Уравнение неразрывности
- •1.5. Обобщенный закон трения
- •1.6. Уравнение движения жидкости
- •1.7. Основы теории подобия
- •1.7.1. Теоремы подобия
- •1.7.2. Соотношения между множителями подобного преобразования и получение критериев подобия
- •1.7.3. Получение критериев подобия методом масштабных преобразований
- •1.7.4. Уравнения подобия
- •Гидростатика
- •2.1. Основное уравнение гидростатики. Закон Паскаля
- •2.2. Давление жидкости на плоскую и криволинейную стенки
- •Определение силы, действующей на наклонную пластину, погруженную в жидкость
- •Давление жидкости на криволинейную поверхность
- •2.3 Основы теории плавания. Закон Архимеда
1.3. Силы, действующие в жидкости
Различают два класса сил, действующих на частицы движущейся или покоящейся жидкости:
объемные (массовые) силы действуют на каждую частицу, находящуюся в рассматриваемом объеме. Примерами таких сил являются силы тяжести, инерции, электростатические и т.п.;
поверхностные силыдействуют на элементы поверхности, ограничивающей выделенный объем. К ним относят силы давления и трения, обусловленного вязкостью жидкости.
П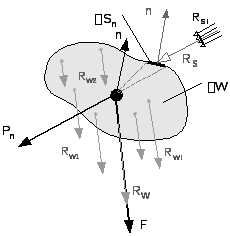 ри
описании силовых взаимодействий в
жидкостях, в отличие от твердых тел,
имеют дело не с самими силами, а с их
плотностями.Плотностью объемных силFв данной точке среды
называют предел отношения главного
вектора объемных силRW,
приложенного к точке, расположенной
внутри малого объема
ри
описании силовых взаимодействий в
жидкостях, в отличие от твердых тел,
имеют дело не с самими силами, а с их
плотностями.Плотностью объемных силFв данной точке среды
называют предел отношения главного
вектора объемных силRW,
приложенного к точке, расположенной
внутри малого объема![]() ,
к массе этого объема, при условии, что
объем стремится к нулю, т.е.
,
к массе этого объема, при условии, что
объем стремится к нулю, т.е.
![]() .
.
В системе Си плотность объемных сил Fимеет размерность м/с2. В случае
действия на жидкость силы тяжести,
плотность объемных сил тяжести равна
ускорению свободного падения![]() ;
при равномерном вращении жидкости с
угловой скоростью
;
при равномерном вращении жидкости с
угловой скоростью![]() ,
плотность распределения центробежных
сил равна центробежному ускорению
,
плотность распределения центробежных
сил равна центробежному ускорению![]() .
.
Плотности объемных сил изменяются в
пространстве и времени
![]() .
В проекциях на оси координат вектор
плотности объемных сил представляют в
следующем виде
.
В проекциях на оси координат вектор
плотности объемных сил представляют в
следующем виде
![]() ,
,
где
![]() – единичные векторы (орты), направление
которых совпадает направлением осей
декартовой системы координат.
– единичные векторы (орты), направление
которых совпадает направлением осей
декартовой системы координат.
Поверхностные силы, главный вектор
которых равен
![]() ,
задаютсявектором напряжений
,
задаютсявектором напряжений
![]() ,
приложенным к площадкеSn.
Ориентация этой площадки в пространстве
определяется единичным вектором
,
приложенным к площадкеSn.
Ориентация этой площадки в пространстве
определяется единичным вектором![]() ,
перпендикулярным к ней. Вектор напряжений
равен пределу отношения главного вектора
поверхностных сил к площадиSn,
на которую он действует, при условии,
что величина этой площади стремится к
нулю
,
перпендикулярным к ней. Вектор напряжений
равен пределу отношения главного вектора
поверхностных сил к площадиSn,
на которую он действует, при условии,
что величина этой площади стремится к
нулю
![]() .
.
Индекс у вектора напряжения
![]() указывает на конкретную площадку,
заданную нормалью
указывает на конкретную площадку,
заданную нормалью![]() ,
в пределах которой действуют рассматриваемые
напряжения. Поскольку через заданную
точку пространства можно провести
бесчисленное множество площадок, то
вектор напряжений в каждой точке
пространства принимает бесчисленное
множество значений в зависимости от
ориентации площадки, к которой приложено
напряжение, и векторного поля не образует.
Направление вектора
,
в пределах которой действуют рассматриваемые
напряжения. Поскольку через заданную
точку пространства можно провести
бесчисленное множество площадок, то
вектор напряжений в каждой точке
пространства принимает бесчисленное
множество значений в зависимости от
ориентации площадки, к которой приложено
напряжение, и векторного поля не образует.
Направление вектора
![]() по отношению к площадкеSnможет быть произвольным. При анализе
его раскладывают на нормальную и
касательную составляющие.
по отношению к площадкеSnможет быть произвольным. При анализе
его раскладывают на нормальную и
касательную составляющие.
В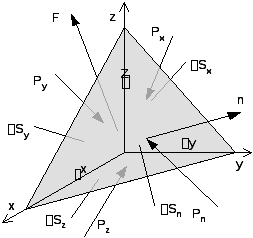 ыделим
в движущейся жидкости элементарный
объем
ыделим
в движущейся жидкости элементарный
объем![]() в виде тетраэдра, грани которогоSx,SyиSzлежат в координатных плоскостях, а
стороныx,y,z,
совпадающие с осями координат, представляют
собой малые величины первого порядка
(01). ГраньSnперпендикулярна орту
в виде тетраэдра, грани которогоSx,SyиSzлежат в координатных плоскостях, а
стороныx,y,z,
совпадающие с осями координат, представляют
собой малые величины первого порядка
(01). ГраньSnперпендикулярна орту![]() .
.
На жидкость, находящуюся в выделенном
объеме, действуют массовые силы, заданные
вектором плотности F,
и поверхностные силы, определяемые
напряжениями![]() ,
которые действуют на гранях тетраэдра,
перпендикулярных осямx,y,zи
нормали
,
которые действуют на гранях тетраэдра,
перпендикулярных осямx,y,zи
нормали![]() ,
соответственно. Если к этим силам
добавить силу инерции
,
соответственно. Если к этим силам
добавить силу инерции![]() ,
то в соответствии с принципом Даламбера
получим
,
то в соответствии с принципом Даламбера
получим
![]() ,
,
где
![]() – вектор ускорения.
– вектор ускорения.
В данном уравнении массовые силы являются
малыми величинами третьего порядка (в
качестве сомножителя имеют
![]() – произведение трех сколь угодно малых
величин). Поверхностные силы представляют
собой малые величины второго порядка
(
– произведение трех сколь угодно малых
величин). Поверхностные силы представляют
собой малые величины второго порядка
(![]() ).
Пренебрегая массовыми силами, а также
учитывая, что
).
Пренебрегая массовыми силами, а также
учитывая, что
![]()
получим
![]() . (1.4)
. (1.4)
Из уравнения (1.4) следует, что напряжение на любой площадке Snможно выразить через напряжения на трех взаимно перпендикулярных площадках, которые могут лежать в координатных плоскостях. В проекциях на оси координат (1.4) имеет вид
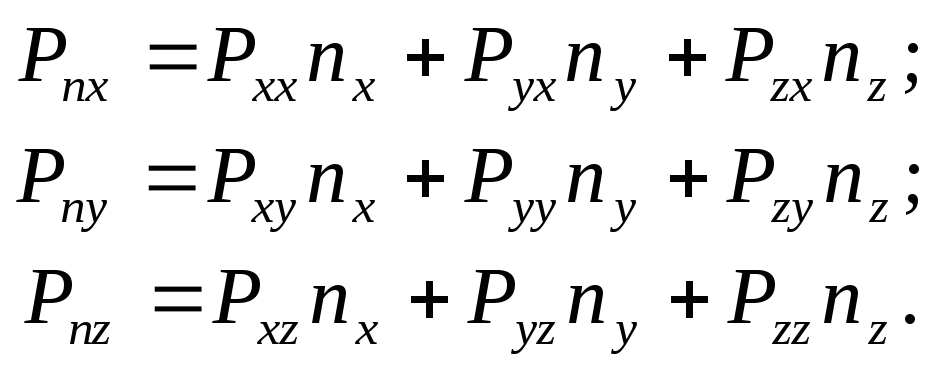 (1.5)
(1.5)
Для обозначения проекции вектора
напряжения используют два индекса:
первый определяет ориентацию в
пространстве площадки, на которую
действует напряжение, направлением
нормали к ней, а второй – ось, на которую
проектируется вектор. Например, Pxy
представляет собой проекцию на осьyвектора напряжения
![]() ,
действующего на площадке, перпендикулярной
к осиx.
,
действующего на площадке, перпендикулярной
к осиx.
Величины
![]() представляют собой нормальные напряжения
к площадкам перпендикулярным осямx,yиzсоответственно, а проекции, в обозначениях
которых присутствуют разноименные
индексы, определяют касательные
напряжения.
представляют собой нормальные напряжения
к площадкам перпендикулярным осямx,yиzсоответственно, а проекции, в обозначениях
которых присутствуют разноименные
индексы, определяют касательные
напряжения.
Совокупность девяти величин типа Pij, связанных соотношением (1.5) образуют матрицу, получившую название тензора напряженийР
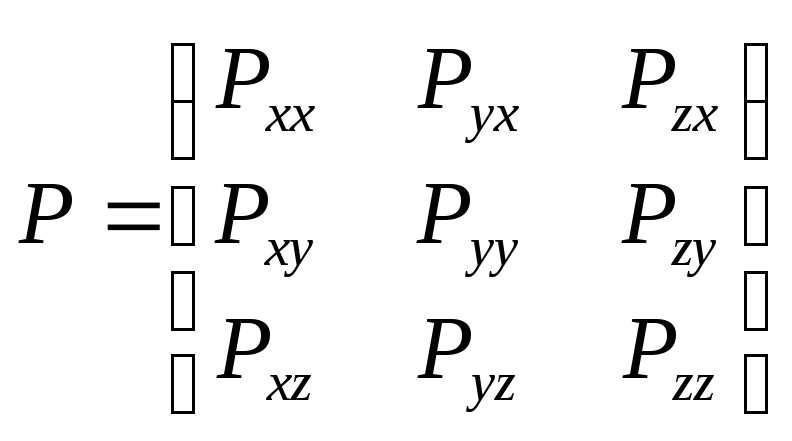 .
.
Напряженное состояние в каждой точке
жидкости описывается тензором напряжений.
Для определения вектора напряжения,
действующего на площадке, проходящей
через рассматриваемую точку, необходимо
знать тензор напряжений Ри ориентацию
площадки в пространстве![]() .
Уравнения (1.4) и (1.5) могут быть представлены
в следующей форме
.
Уравнения (1.4) и (1.5) могут быть представлены
в следующей форме
![]() . (1.6)
. (1.6)
