
- •ОГЛАВЛЕНИЕ
- •Введение
- •Используемые единицы измерений и основные константы
- •1.1. Предпосылки возникновения волновой механики
- •1.1.2. Теория строения атома Бора
- •1.1.3. Корпускулярно-волновой дуализм свойств материи
- •1.1.4. Принцип неопределенности
- •1.2. Волновая (квантовая) механика
- •1.3. Квантово-механическая модель атома
- •1.3.1. Основное состояние атома водорода
- •1.3.2. Радиальное распределение электронной плотности. Электронная орбиталь
- •1.3.4. Многоэлектронные атомы
- •1.3.5. Электронные конфигурации многоэлектронных атомов
- •1.3.6.Связь периодического закона со строением атома
- •1.3.7.Физико-химические характеристики атома
- •2.1. Основные характеристики химической связи. Классификация моделей описания химической связи
- •2.2. Ковалентная химическая связь
- •2.2.1. Метод валентных связей (ВС)
- •2.2.3. Геометрия простейших молекул. Гибридизация АО
- •2.2.4. Донорно-акцепторный механизм образования ковалентной связи
- •2.3. Полярность связи. Дипольный момент молекулы
- •3.1. Агрегатные состояния
- •3.3.1.Основные понятия о строении кристаллов
- •Библиографический список

1.2. Волновая (квантовая) механика
1.2.1.Волновое уравнение. Уравнение Шредингера
Уравнение, которое будет описывать движение электрона, должно удовлетворять следующим требованиям: отражать волновой характер движения электрона и содержать в себе характеристики электрона как частицы.
Для описания волновых свойств электрона можно использовать известное из математики и физики дифференциальное уравнение второго порядка (уравнение волнового процесса):
∂2Ψ + ∂2Ψ + ∂2Ψ = 1 ∂2Ψ ,
∂x2 ∂y2 ∂z2 v2 ∂t2
v – скорость распространения волны.
Ψ(x,y,z,t) – пси-функция – волновая функция, которая зависит от координат и времени и может быть представлена в виде синуса, косинуса, экспоненты или любой другой функции, являющейся решением дифференциального уравнения волнового процесса.
Для простоты написания левую часть уравнения представляют обычно в операторной форме:
|
|
|
|
|
2 |
Ψ= |
1 |
|
∂2Ψ |
, |
|
|
|
|
|
|
|
|
|
|
∂t2 |
||
|
∂2 |
∂2 |
v2 |
||||||||
|
∂2 |
|
|
|
|
|
|||||
где |
|
+ |
|
+ |
|
= 2 – оператор Лапласа (читается "набла два"). |
|||||
∂x2 |
∂y2 |
∂z2 |
|||||||||
Чаще всего интерес представляют стационарные процессы (стоячие волны). Описывающее их уравнение содержит функцию, не зависящую от времени. Поэтому волновое уравнение преобразуют, исключая зависимость от времени. Делается допущение, что волновую функцию можно представить в виде произведения двух функций, одна из которых зависит только от координат (Ψ(x,y,z)), а другая только от времени (G(t)):
Ψ(x,y,z,t) = Ψ(x,y,z) G(t).
Волновое уравнение приобретает вид
G(t) 2Ψ(x, y, z) = |
1 |
Ψ(x, y, z) |
d 2G(t) |
. |
v2 |
|
|||
|
|
dt2 |
||
G(t) не зависит от координат, поэтому выносится за знак дифференцирования в левой части уравнения, а Ψ(x,y,z) не зависит от времени – выносится за знак дифференцирования в правой части.
16
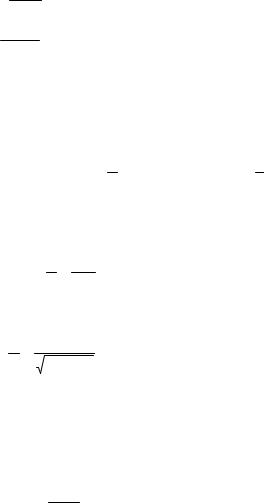
Из теории волновых процессов известно, что функцию G(t) можно представить в виде
G(t) = А cos(2π ν t),
где ν - частота волнового процесса. Дважды дифференцируя G(t) по времени:
G(t) = А cos(2π ν t) ≠ 0, dGdt(t) = −A 2π ν sin(2πνt) ,
d 2G(t) = −A 4π2 ν2 cos(2πνt) dt2
и подставляя вторую производную G(t) в уравнение волнового процесса, получаем
А cos(2π ν t) 2Ψ(x,y,z) = (1/v2) Ψ(x,y,z) (-A 4π2ν2) cos(2π ν t),2Ψ(x,y,z) = -(4π2ν2/v2) Ψ(x,y,z),
2Ψ(x,y,z) + (4π2ν2/v2) Ψ(x,y,z) = 0.
Поскольку частота волнового процесса равна скорости распростране-
ния волны, деленной на длину волны: ν = λv , и соответственно νv = λ1 , то
2Ψ(x,y,z) + (4π2/λ2) Ψ(x,y,z) = 0
В полученном уравнении длину волны частицы можно заменить такими ее характеристиками, как масса и кинетическая энергия, используя уравнение де Бройля.
Длина волны де Бройля λ = hp = mh v .
Кинетическая энергия электрона |
Eк |
= |
mv2 |
= |
(mv)2 |
= |
p2 |
, |
|||||
2 |
2m |
2m |
|||||||||||
|
|
|
|
|
|
|
|
||||||
h |
|
h |
, λ2 |
= |
|
h2 |
|
|
|
|
|
||
λ = p = |
|
|
|
|
|
|
|
||||||
2 m Eк |
|
2 m Eк |
|
|
|
|
|||||||
2Ψ(x, y, z) + |
8π2m |
Eк Ψ(x, y, z) = 0 . |
|
|
|
||||||||
h2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Как правило, при описании состояния электрона определяют полную энергию. Поскольку кинетическая энергия электрона равна разности между полной энергией (E) и его потенциальной энергией (V): Eк = E – V, то можно записать
2Ψ(x, y, z) + 8π2m (E −V ) Ψ(x, y, z) = 0 . h2
17

Таким образом, получается волновое уравнение, независимое от времени, содержащее в качестве параметра массу электрона, характеристику электрона как частицы. Это уравнение известно как уравнение Шрёдингера, названное по имени австрийского физика Эрвина Шрёдингера (Schrödinger), который его предложил в 1926 г. для описания состояния микрочастицы в потенциальном поле.
Прежде чем решать уравнение Шредингера для конкретных систем, выясним физический смысл волновой функции. Раскрыть его достаточно непросто, поскольку в макромире нет аналогий корпускулярно-волновым свойствам микрообъектов. И до некоторой степени волновая функция представляет собой математическую абстракцию.
В 1926 г. Макс Борн (Born), применив вероятностные идеи принципа неопределенности, дал общепринятую в настоящее время трактовку физического смысла волновой функции. Во-первых, сама волновая функция физического смысла не имеет, но связана с вероятностью нахождения частицы в данном элементе пространства. Во-вторых, вероятность нахожде-
ния частицы (dP) в элементарном объеме (dV) пропорциональна квадрату волновой функции:
dP = Ψ2(x,y,z) dV.
Величина dVdP
теризует вероятность нахождения частицы в элементарном объеме пространства с координатами x,y,z. Для электрона ее часто называют электронной плотностью.
Вероятность нахождения частицы в каком-либо конечном объеме V равна интегралу квадрата волновой функции по данному объему:
PV = ∫Ψ2 (x,y,z)dV .
V
Вероятность должна выражаться действительным положительным числом, меньшим или равным единице. Сама же волновая функция может быть положительной, отрицательной или мнимой, поэтому в общем виде используется не квадрат волновой функции, а квадрат ее модуля.
Такое толкование физического смысла волновой функции является одним из постулатов квантовой механики. Правомерность такой интерпретации подтверждается соответствием экспериментально определенного взаимного расположения атомов в молекулах и квантово-механического расчета.
Из условия, что вероятность события не может быть больше единицы,
следует принцип нормирования волновых функций. Вероятность на-
хождения частицы во всем рассматриваемом объеме должна быть равна единице (частица находится в этом объеме – событие достоверное):
18

P = ∫A2Ψ2 (x,y,z)dV =1 ,
V
А – нормирующий множитель, коэффициент, входящий в волновую функцию, который подбирается таким образом, чтобы выполнялось условие нормировки.
1.2.2.Решение уравнения Шредингера для простейших случаев
Решение уравнения Шредингера даже для относительно простых реальных объектов, таких как атомы и молекулы, содержащих два и более электронов, изучаемых в теории строения атома и химической связи, представляет собой сложную математическую задачу. Для того чтобы понять характер и особенности результатов квантово-механического описания состояния электрона в атомах и молекулах, решим строго простейшую задачу нахождения электрона в так называемом "потенциальном ящике" – некоторой ограниченной области пространства, вне которой потенциальная энергия электрона обращается в бесконечность. Электрон не может покинуть пределы "потенциального ящика", то есть находится в связанном состоянии. Это, по сути своей, является моделью нахождения электрона в атоме.
Электрон в одномерном потенциальном ящике.
Рассмотрим состояние электрона в одномерном потенциальном ящике (рис. 1.3). Движение электрона происходит только вдоль оси X. Внутри ящика потенциальная энергия частицы принимается равной нулю (потенциальную энергию можно отсчитывать от любого выбранного уровня), вне его она равна бесконечности, то есть частица находится внутри ящика и не может покинуть его пределы.
|
|
|
|
E |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V=∞ |
|
|
|
V=0 |
|
|
V=∞ |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
a |
|
|
|||||
Рис. 1.3. Электрон в одномерном потенциальном ящике: a - параметр (размер) потенциального ящика
С точки зрения классической механики частица, находящаяся в потенциальном ящике, может иметь в принципе любую энергию и находиться в любой точке ящика. При квантово-механическом рассмотрении ситуация
19

меняется. Состояние электрона описывается уравнением Шредингера, и его характеристики (энергия и вероятность нахождения в пространстве) получаются при решении этого уравнения.
Как и любое дифференциальное уравнение, уравнение Шредингера имеет бесконечное множество решений. Физический смысл имеют лишь некоторые из них. В нашем случае волновая функция описывает реальную физическую систему, поэтому она должна соответствовать следующим условиям:
•конечность – вероятность нахождения электрона в пространстве не может быть больше единицы;
•однозначность – вероятность нахождения электрона в точке однозначна;
•непрерывность – нет особых точек в пространстве.
Волновые функции, удовлетворяющие этим условиям, называются собственными функциями, а соответствующие им значения энергий – собственными значениями энергий.
Поскольку электрон находится внутри одномерного «ящика» (V=0), уравнение Шредингера приобретает вид
d 2Ψ(x) + 8π2m E Ψ(x) = 0 . dx2 h2
Известно, что решением данного типа уравнения может быть функция
Ψ(x) = A sin 2λπ x – общее решение. В принципе вид функции может быть
идругим, но она должна быть непрерывной, однозначной и конечной. Используя общее решение, граничные условия нашей задачи и прин-
цип нормировки, можно получить волновую функцию, описывающую состояние электрона в потенциальном ящике.
Граничными условиями является равенство волновой функции нулю на стенках:
Ψ(0) = A sin 2λπ 0 = 0 , Ψ(a) = A sin 2λπ a = 0 .
Поскольку амплитуда волновой функции не равна нулю, то из второго
условия следует: |
|
|
2a |
|
|
π n |
|
||
sin |
2π |
a = 0 , |
2π |
a = π n , n=1,2,3….., λ = |
, |
Ψ(x) = A sin |
x . |
||
|
|
n |
|
||||||
|
λ |
λ |
|
|
a |
||||
Значение амплитуды А находят из условия нормировки. Поскольку электрон находится в потенциальном ящике, то интеграл квадрата волновой функции по координате ящика (от 0 до a) равен единице:
20
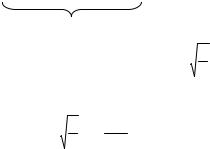
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
|
|
|
2 |
|
|
πn |
|
|
|
|
|
|
|
|
|
1 |
|
|
a |
|
|
π n |
|
|||||||
∫Ψ |
(x)dx =1, |
∫A |
sin |
( |
|
x)dx =1, |
|
2 |
|
|
)dx, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= ∫sin |
( |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
a |
|
|||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π n |
|
x =U , dU = |
|
π n |
dx , |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
a |
|
π n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
|
|
∫sin2 UdU = |
|
|
[ |
U − |
|
sin 2U ] |
|
|
= |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
A2 |
|
|
π n |
|
|
π n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
= |
|
|
a |
[ |
π n |
x − |
|
1 |
sin |
|
π n |
x cos |
π n |
x] |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
π n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
2 |
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
при x=0 и x=a |
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
= |
|
|
a |
|
|
[ |
π n |
a] |
= |
a |
|
|
|
|
|
|
|
→ |
|
|
|
|
A = |
|
2 . |
||||||||||||||||
|
|
|
|
A2 |
|
|
π n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||||||||||
Таким образом, выражение для волновой функции электрона в одно-
мерном потенциальном ящике имеет вид |
|
|
Ψ(x) = |
2 sin |
π n x , |
|
a |
a |
где a – параметр потенциального ящика; |
n = 1,2,3…– целочисленный |
|
параметр. То есть состоянию электрона в потенциальном ящике соответствует набор волновых функций, отличающихся целочисленным парамет-
ром n, называемым квантовым числом.
Для определения энергии электрона проделаем следующие математические операции.
1. Поскольку в уравнение Шредингера входят волновая функция, и ее
вторая производная, запишем их: |
|
|
|
|
π n |
|
|
|
|
|
|||||
|
|
Ψ(x) = A sin |
x , |
|
|
|
|||||||||
|
|
|
|
||||||||||||
|
|
dΨ(x) |
|
|
π n |
|
|
a |
π n |
|
|
||||
|
|
= A |
cos |
x |
, |
||||||||||
|
|
dx |
|
a |
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
||||
|
d 2 Ψ(x) |
= A |
π2 n 2 |
|
(−sin |
π n |
x) . |
||||||||
|
dx 2 |
|
a 2 |
|
|
a |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
2. Подставим выражения волновой функции и ее второй производной в уравнение Шредингера, описывающее состояние электрона внутри потен-
циального ящика: |
|
|
|
|
|
|
|
|
|
|
||
A |
π2 |
n 2 |
(−sin |
π n |
x) + |
8π2 |
m |
E A sin |
π n |
= 0 |
, |
|
a 2 |
a |
h |
2 |
a |
||||||||
|
|
|
|
|
|
|||||||
21
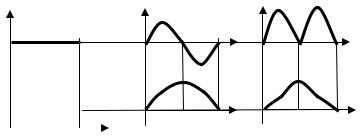
A (sin |
π n |
x) [− |
π2 n2 |
+ |
8π2 m |
E] = 0 . |
|
a |
a 2 |
h 2 |
|||||
|
|
|
|
3. Поскольку волновая функция внутри ящика не равна нулю:
( Ψ(x) = A sin |
π n |
x |
≠ 0 ), то − |
π2 n2 |
+ |
8π2 |
m |
E = 0 |
, |
||
a |
a 2 |
h |
2 |
||||||||
|
|
|
|
|
|
|
|||||
|
E = |
h2 |
n2 , n=1,2,3… |
|
|
|
|||||
|
8a 2 m |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
То есть набору волновых функций соответствует набор энергий.
Из полученных результатов решения следуют особенности квантовомеханического описания состояния электрона в потенциальном ящике.
1.Электрон, находясь в потенциальном ящике, может иметь толь-
ко дискретные значения полной энергии E1, E2, E3…, величины которых определяет целочисленный параметр n = 1,2,3…, называемый квантовым числом. То есть энергия связанного электрона квантована.
2.Распределение вероятности нахождения электрона в объеме потенциального ящика (плотность вероятности) определяется его энергетическим состоянием – энергией, которой обладает электрон.
Графическая интерпретация выводов (рис.1.4).
E |
1) |
|
ψ(x) |
|
2) |
ψ2(x) |
|
3) |
|
|
n=2 |
E2 |
|
|
a |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
x |
0 |
|
a |
x |
||
|
|
|
|
|
|
|||||
n=1 |
E1 |
0 |
a/2 |
a |
x 0 |
a/2 |
a |
x |
||
|
|
|
|
|||||||
0 |
|
a |
x |
|
|
|
|
|
|
|
Рис. 1.4. Первое и второе энергетическое состояние электрона в одномерном потенциальном ящике. Полная энергия Еi (1), соответствующая ей волновая функция Ψi(x) (2) и плотность вероятности Ψi2(x) (3) электрона
1. Энергия электрона, находящегося в потенциальном ящике, не зави-
сит от координаты и может принимать значения En |
= |
h 2 |
n 2 , где a – |
|
8a 2 m |
||||
|
|
|
параметр ящика; m – масса частицы; n – целочисленный параметр.
2. Плотность вероятности для электрона в ящике (распределение вероятности нахождения электрона в различных точках объема)
22

dP(x)
dx
Электрон в трехмерном потенциальном ящике. Вырожденные энергетические состояния.
Задача о нахождении частицы в трехмерном потенциальном ящике аналогична предыдущей, их граничные условия полностью совпадают: волновая функция на границах ящика обращается в ноль, потенциальная энергия внутри ящика равна нулю (V=0), а за пределами ящика – бесконечности (V=∞), то есть частица находится в трехмерном потенциальном ящике и не может покинуть его. Единственным отличием является то, что волновая функция для частицы в трехмерном потенциальном ящике является функцией трех пространственных координат: Ψ(x,y,z).
Уравнение Шредингера для данного случая представляет собой дифференциальное уравнение в частных производных с тремя переменными:
∂2Ψ(x, y, z) |
+ |
∂2Ψ(x, y, z) |
+ |
∂2Ψ(x, y, z) |
+ |
8π2 m |
E Ψ(x, y, z) = 0 . |
|
∂x2 |
∂y2 |
∂z2 |
h2 |
|||||
|
|
|
|
Стандартным приемом, которым пользуются при решении такого типа уравнений, является разделение переменных: представление волновой функции в виде произведения трех функций, каждая из которых зависит только от одной координаты:
Ψ(x, y, z) = X (x) Y ( y) Z (z) ,
Y(y) Z(z) d2X2(x) +X(x) Z(z) |
d2Y(y) |
+ X(x) Y(y) d2Z2(z) = |
||||||||||||||||
2 |
||||||||||||||||||
|
|
|
dx |
|
|
|
|
|
dy |
|
|
|
dz |
|||||
|
|
|
|
=− |
8π2 m |
E X(x) Y(y) Z(z), |
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
d2 X(x) |
1 |
|
|
d2Y(y) |
1 |
|
d2Z(z) |
|
8π2 m |
E . |
||||||
|
|
|
+ |
|
|
|
+ |
|
|
|
=− |
|
|
|||||
X(x) |
dx2 |
Y(y) |
dy2 |
Z(z) |
dz2 |
h2 |
|
|||||||||||
Поскольку правая часть уравнения не зависит от координат, то можно представить полную энергию электрона как сумму трех энергий: E = Ex + +Ey + Ez. Уравнение Шредингера при этом преобразуется в три дифференциальных уравнения, аналогичных волновым уравнениям электрона в одномерном ящике, решение которых уже получено:
1 |
|
d 2 X (x) |
= − |
8π2 m |
Ex , |
||||
X (x) |
dx2 |
|
h2 |
|
|||||
|
|
|
|
|
|||||
|
1 |
|
d 2Y(y) |
= − 8π2 m |
Ey , |
||||
|
Y(y) |
dy2 |
|
||||||
|
|
|
|
h2 |
|
|
|||
23
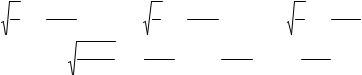
|
|
|
|
|
|
1 |
|
|
d 2Z(z) |
= − |
8π2 m Ez . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Z(z) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
dz2 |
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Для волновой функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
X (x) = |
2 |
sin |
n |
x |
π |
x , Y ( y) = |
|
2 |
|
sin |
ny π |
y , Z (z) = |
2 |
sin |
n |
z |
π |
z , |
|||||||||||
a |
|
|
|
b |
|
|
b |
c |
|
c |
|||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ψ(x, y, z) = |
8 |
|
sin( |
n |
x |
π |
x) sin( |
ny π |
|
y) sin( |
n |
z |
π |
z) , |
|
|||||||||||||
|
a b c |
|
|
|
|
b |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|||||
a,b,c – параметры трехмерного потенциального ящика (размеры – длина, ширина, высота); nx, ny, nz – целочисленные параметры – «квантовые числа». Необходимо отметить, что каждой координате соответствует свое квантовое число.
Для энергии:
|
h2 |
2 |
|
|
|
|
|
|
h2 |
|
|
2 |
|
|
|
|
|
h2 |
2 |
|
|
Ex = |
|
nx |
, |
Ey = |
|
|
|
|
|
ny |
|
, |
|
|
|
Ez = |
|
nz |
, |
||
8m a2 |
8m |
b2 |
|
|
|
|
8m c2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
E = |
h2 |
( |
n |
x |
2 |
+ |
ny 2 |
+ |
n |
z |
2 |
) . |
|
|
|
||
|
|
|
|
8m |
a2 |
b2 |
c2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Из полученных результатов решения следует:
1.Энергия электрона в трехмерном потенциальном ящике кванто-
вана.
2.Каждое энергетическое состояние электрона определяется набором из трех квантовых чисел.
Однако в реальных системах часто встречается ситуация, когда определенное энергетическое состояние (энергия частицы) может быть описано не единственным набором квантовых чисел, то есть более чем одной волновой функцией. Тогда говорят о вырождении энергетического состояния.
Проиллюстрировать явление вырождения по энергии можно на примере частицы в трехмерном потенциальном ящике. Если рассмотреть энергетические состояния частицы в ящике, который представляет собою куб (а=b=c), то выражение для энергии приобретает вид
|
h2 |
2 |
2 |
2 |
|
|
E = |
|
(nx |
+ ny |
+ nz |
) |
|
8m a 2 |
||||||
|
|
|
|
|
а – параметр куба (величина ребра).
Составим энергетическую диаграмму состояния частицы в таком ящи-
ке, откладывая по вертикальной оси энергию частицы в единицах |
h2 |
|
8m a2 |
||
(рис.1.5). |
||
|
24
