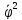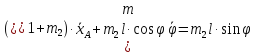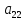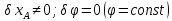РГР7 _Л_ книга_Пр_вар 3
.docx
РГР7_ Л_книга, Пример, вар 3
Исходные данные:
Ползун
1 массой m1
скользит без трения по горизонтальной
направляющей. К ползуну подвешен
математический маятник 2 длиной l
и массой m2,
связанный с ползуном спиральной пружиной
с крутильной жесткостью С..
При нижнем положении маятника пружина
не деформирована. К точке B
маятника приложена постоянная
по величине сила
 ,
составляющая угол
с горизонтом . Угол
линейно меняется со временем
,
составляющая угол
с горизонтом . Угол
линейно меняется со временем
 .Составить
дифференциальные уравнения движения
системы и рассчитать конкретное движение
на ЭВМ.
.Составить
дифференциальные уравнения движения
системы и рассчитать конкретное движение
на ЭВМ.
Исходные данные:
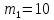 кг;
кг;
 кг;
кг;

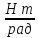 ;
;
 Н;
Н;

 ;
;
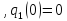 м;
м;
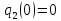 м;
м;
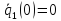
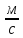 ;
;

 .
.

Система
имеет две степени свободы
 .
.
Постановка задачи:
Уравнения Лагранжа II рода:
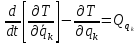 ,
,
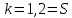
Здесь
Обобщённые
координаты:
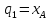 ;
;

Обобщённые
скорости:
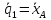 ;
;
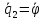 .
.
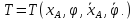 -кинетическая
энергия системы;
-кинетическая
энергия системы;
обобщённые
силы
 и
и
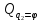 ,
соответствующие обобщенным координатам
,
соответствующие обобщенным координатам
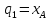 ;
;
 .
.
Что входит в рассматриваемую механическую систему:
-
Ползун 1 (
 )
)
 поступательное движение
поступательное движение
 ;
;
-
Маятник 2 (
 )
)
 мат.
точка
мат.
точка
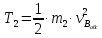
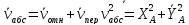 ;
;
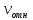 =
=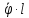 ;
;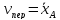
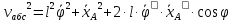
Кинетическая энергия системы:
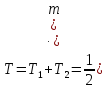
Уравнения Лагранжа II рода:
 ,
,
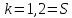
|
|
II
урав-е
по второй об. к-те
|
|
I |
II |
|
I-1)
|
II-1)
|
|
I-2)
|
II-2)
|
|
I-3)
|
II-3)
|
Окончательно уравнения Уравнения Лагранжа П-го рода::
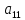

В
матричной форме
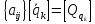 ,
,
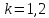 получим:
получим:
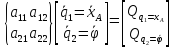
инерциальная матрица, квадратная, симметричная относительно главной диагонали матрица инерционных коэффициентов, где все:
 ,
если
,
если
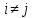 ,
т.е.
,
т.е.

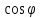 ;
;
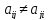 ,
если
,
если
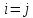 ,
т.е.
,
т.е.
 ;
;
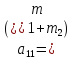 ,
,
 .
.
-
Виртуальная работа от 2-х типов сил:
-
от всех заданных активных сил:
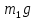 ,
,
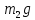 ,
,
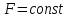 ;
;
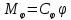
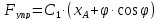 ;
;
-
от сил трения
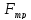 ;
по условию задачи равны нулю.
;
по условию задачи равны нулю.
Определение
обобщённых сил
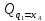 и
и
 , соответствующих обобщенным координатам.
, соответствующих обобщенным координатам.
 (5)
(5)
Для
определения обобщенных сил
 и
и
 ,
соответствующих обобщенным координатам
,
соответствующих обобщенным координатам
 восспользуемся
методом независимости (замораживания):
восспользуемся
методом независимости (замораживания):
Так
как обобщенные координаты
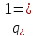
 и
и
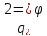 независимые
друг от друга параметры, то и их вариации
независимые
друг от друга параметры, то и их вариации
 и
и
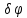 –
тоже не зависятдруг от друга, поэтому:
–
тоже не зависятдруг от друга, поэтому:
Поэтому системе можно сообщить такое перемещение, чтобы

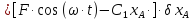 ;
сравнивая полученное выражение с
;
сравнивая полученное выражение с ,
находим
,
находим
 .
.
 :
:
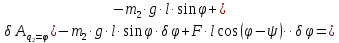
 ;
сравнивая с
;
сравнивая с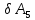 ,
получим:
,
получим:
 .
.
Окончательно уравнения Лагранжа П-го рода , описывающие движение рассматриваемой несвободной системы с двумя степенями свободы, записываются следующим образом:
I
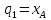 ;
;
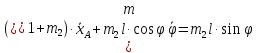
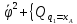 =
=


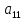
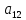
=
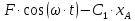 };
};
II

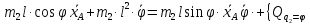 =
=

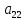
=
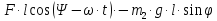 .}.
.}.
__________________________________________________________

 :
: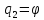

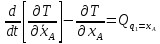


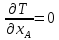



 --
--