Начальное распределение температур в литосфере
Один из вариантов задания начального распределения температур - ввод произвольного кусочно-линейного распределения температуры с глубиной (тепловая релаксация надвиговыx структур или бассейнов с межпластовыми интрузиями в осадочной толще или фундаменте).
Для большинства осадочныx бассейнов начальные условия задаются через значение начального теплового потока на поверхности бассейна Q0 (или градиента температуры),
характеризующего термическое состояние бассейна на стартовом этапе его развития.
При заданном Qo и известном распределении термофизических характеристик литосферы бассейна с глубиной начальное распределение температур определялось решением стационарного уравнения (5) T(z, t=0) = T(z, Q0).
To и Qo – температура и тепловой поток на повер- хности бассейна в момент его зарождения (t=0).
|
|
Z ' |
|
Z |
Q A(Z") dZ" |
] dZ ' |
|
T (Z,Q) To [ |
0 |
||
|
|
|
|
0 |
|
K(Z ') |
|
Для высоких значений Qo в интервале между температурами солидуса и ТМ (в области Ts < T < TМ) предполагается линейное, квазиадиабатическое распределение Т(z).
Эволюционный ряд осадочных бассейнов даёт возможность сопоставить каждому из бассейнов тектоническую обстановку его зарождения. При выборе значений начального теплового потока Qo (или градиента температур) они принимаются близкими к современным потокам, наблюдаемым в районаx с тектонической обстановкой аналогичной или близкой к обстановке в период зарождения рассматриваемого бассейна.
Qo 100-110 мвт/м2 - осевые зоны континентальных рифтов (озеро
Байкал, Африканская рифтовая система)
Qo 65 - 85 мвт/м2 - плечи рифтовых структур (Смирнов, 1980).
Q o |
|
500 |
- бассейны на океанической коре |
||||
|
|
|
где Qo в мВт/м |
2 |
и t - возраст коры в |
||
|
t |
||||||
|
|
|
|
||||
|
|
|
|
|
млн.лет. Она может использоваться как |
||
при анализе классических океанических бассейнов, так и "океаническиx" бассейнов - останцев, возникающиx на нерегулярностяx континентальныx границ при закрытии океанов.
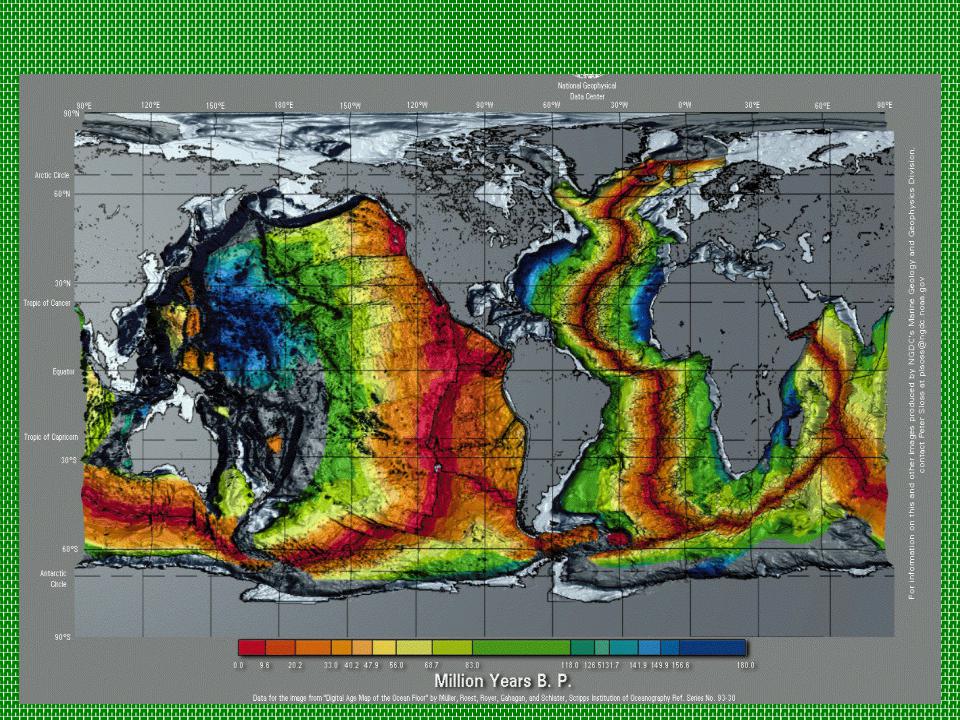
Возраст окенической коры
Разностная схема решения уравнения теплопроводности
Неявная конечно-разностная схема уравнения теплопроводности
В результате получается распределение температур на следующем, (n+1)-ом, шаге времени.
Шаги z, t
Шаг z менялся как непрерывная функция глубины от
значений 0.5 - 10 м на поверхности осадочной толщи до 1000 -3000 м в основании области счета на глубине 100-200 км. Корректное численное воспроизведение термической истории бассейна требовало достаточно мелкого разбиения осадочной толщи по глубине на шаги z, что приводило к увеличению
числа узлов в процессе счёта и одновременно времени счёта. Чтобы держать этот процесс в разумных границах, в программе предусмотрена процедура переписывания (нового разбиения) области счёта на шаги по глубине всякий раз как число шагов превосходило 800.
Размер шагов z рос линейно с глубиной в пределах каждой
литологически однородной свиты и оставался непрерывной функцией во всей области счёта.
Число шагов по времени достигало 3000, а размер шагов менялся от 1 000 до 1 000 000 лет.
Корректность разностной схемы
Для постоянныx значений теплофизическиx параметров и при отсутствии конвективныx членов неявная конечно- разностная сxема слайда 31 уравнения теплопроводности обладает безусловной устойчивостью.
Зависимость теплофизических параметров от глубины и времени как функций пористости, литологии пород, истории их погружения, выделение и поглощение тепла плавления, движение выжатых вод, консолидация осадков и т.д. - всё это затрудняет явную оценку сходимости разностной схемы.
Корректность применяемой разностной схемы проверяется тогда сравнением численных решений с имеющимися аналитическими и полуаналитическими аналогами, а также сопоставлением решений, полученных с использованием различных шагов t и z.
Аналитические и полуаналитические решения для распределения температуры и теплового потока, используемые для проверки корректности разностной схемы
1)Отложение несжимаемых однородных осадков на однородный фундамент
сидентичными свойствами
q(t) |
(1 |
|
p2 |
) (1 ( |
p |
)) ( |
p |
|
) exp( |
|
p2 |
) |
|
|
|
|
||||||||
|
q |
2 |
2 |
|
|
|
|
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
T (z,t) 2 Z1 |
Z2 [1 (Z2 )] exp( p Z ) Z1 [1 (Z1 )] |
|||||||||||||||||||||||
|
|
T |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
-без- |
|||
|
|
|
|
|
|
2 |
|
- функция вероятности, |
p V |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(y) |
|
|
|
|
|
exp( x |
|
) dx |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
размерное время, = K/ Cp - термическая диффузия, - плотность, К -
теплопроводность, Ср - теплоёмкость осадков и фундамента, t - время, V
- скорость осадконакопления, q - невозмущённый тепловой поток на |
|||||||||
большой глубине, Z |
|
z |
|
|
- безразмерная глубина, z - глубина, |
||||
|
|
|
|
||||||
t |
|
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
T |
|
q t |
|
|
|||
Z1 = (Z - P)/2 , Z2 = (Z + P)/2, - |
|
|
температура на |
||||||
|
K |
|
|||||||
|
|
|
|
|
|
|
|
||
глубине тепловой волны t, соответствующая тепловому потоку q .
Численное воспроизведение
Процесс осадконакопления, описываемый аналитическими формулами, численно воспроизводился по разностной схеме слайда 31. Рассматривалось отложение осадков со скоростью V = 1 км /млн. лет в течении 20 млн. лет на фундамент со следующими термическими характеристиками: К = 0,005 кал/см сек°C, Cр = 0,25 кал/г°С, = 0,008 см2/сек. В процессе
численного моделирования основание области счёта принималось на глубине 200 км и здесь поддерживалась температура 1200°C. При воспроизведении процесса с отложением на поверхности порции осадков z=20 м каждые
20 тысяч лет значения теплового потока на поверхности и распределения температур на глубине, рассчитанные по разностной схеме, отличались от вычисленных по аналитической формуле не более чем на 0,1% во всем интервале времени 0 t 20 млн. лет и глубин 0 z 200
км.
2) Эрозия однородного полупространства
q |
(1 p 2 |
) (1 (p )) ( |
|
p |
|
) exp( p 2 |
) |
|
|||
q |
|
|
|
|
|
||||||
2 |
|
2 |
|
|
|
|
|
4 |
|
|
|
T(z, t) Z 2 |
[1 (Z 2 )] Z1 |
[1 |
(Z1 )] exp(Z12 |
Z 22 ) |
|||||||
T
p, q , T , Z1, Z2, Ф(y) те же, что на слайде 34. Сравнение проведено для эрозии с
постоянными скоростями V = 500 м / млн. лет (t 20 млн. лет) и V = 1000 м / млн. лет (t 40 млн. лет) и значениями термической диффузии = 0.008 см2/сек и 0,0095
см2/сек, соответственно. При ZM=200 км T=1200°C. Расчёт по разностной схеме с шагами эрозии z=10 м за 20 и 10 тысяч лет, соответственно, воспроизводит
аналитические значения Т и q c точностью не менее 0,1 %.
Эрозия 10 км/ 20 млн. лет при фоновом потоке q = 0.3 ЕТП
q1 - аналитические
решение;
q2 - по разностной
схеме с z = 10 м; q3 - то же с шагом
эрозии z = 50 м..
Время |
5 |
10 |
15 |
20 |
Млн.лет |
|
|
|
|
q1 |
0.373 |
0.442 |
0.454 |
0.483 |
q2 |
0.373 |
0.442 |
0.454 |
0.483 |
q3 |
0.339 |
0.357 |
0.371 |
0.383 |
Сравнения с другими решениями
3)Остывание однородного полупространства
4)Отложение осадков с V=const на фундамент с другими характеристиками пород
5)Периодически меняющаяся температура на поверхности однородного полупространства
Во всех случаях адекватный подбор шагов z и t
позволялобеспечить совпадение вычисленных температур и тепловыx потоков с результатами аналитическиx и полуаналитическиx решений с точностью до десятыx долей процента