
- •1.3 Точность систем телекоммуникаций
- •2.4. Моделирование сигналов рядом Фурье
- •2.5 Моделирование сигналов рядом Котельникова
- •2.7 Моделирование сигналов функциями Уолша
- •2.8 Моделирование сигналов на основе преобразования Фурье
- •2.11 Моделирование сигналов на основе преобразования Лапласа
- •3 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗВЕНЬЕВ СИСТЕМ ТЕЛЕКОММУНИКАЦИЙ
- •3.1 Виды звеньев в системах телекоммуникаций
простых линейных звеньев. Поэтому они применяются при моделировании СТК и измерительных систем во временной области.
Полиномы Эрмита
n t2 t2 (n )
Hn(t ) ( 1) e e , n
обладают следующими свойствами:
являются полиномами с целочисленными
0, |
(2.40) |
вещественными коэффициен-
тами, |
например, H0(t ) 1, |
|
|
|
H1(t ) 2t, |
H2(t ) 4t2 2, |
H3(t ) 8t3 12t , |
|||||||||||||||||||
H4(t ) 16t4 48t2 12; |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
Р |
||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
образуют ортогональную с единичным весом на бесконечном интервале |
|||||||||||||||||||||||||
, |
систему функций Эрмита |
|
|
|
|
|
|
|
И |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
h (t ) e |
t2 2 |
H |
|
(t ), |
|
|
|
|
У |
|
(2.41) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
имеющих норму |
h (t ) |
|
|
|
|
|
n! ; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
в соответствии с условиями теоремы разложения в обобщенный ряд Фу- |
|||||||||||||||||||||||||
рье представляют моделируемую функцию |
|
Б |
|
|
|
|
||||||||||||||||||||
f(t ) на бесконечном интервале |
||||||||||||||||||||||||||
, |
рядом (по функциям Эрмита) |
|
аn |
|
|
|
|
|||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
f(t ) Cnhn(t ), |
к |
|
|
|
|
(2.42) |
||||||||||||||||||
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|||||
|
где с учетом (2.9) C |
|
|
|
2n n! |
|
|
f(t )h (t )dt . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
имеют |
|
|
|
|
|
|
|
|
|
||||||||||
|
2.7 Моделирование сигналов функциями Уолша |
|
|
|
|
|||||||||||||||||||||
|
Рассмотренные в |
подразд |
. |
|
2.5 |
|
и 2.6 ортогональные системы, различаю- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
щиеся видом образуемых их функций, интервалами ортогональности и воз- |
|
и |
одно общее свойство: они состоят из плав- |
можностями использован я, |
|
ных функций, которые не содержат разрывов и изломов. В этом смысле особое место занимает с стема функций Уолша. Она построена из функций с разрыва-
ми первого рода, повторяющих по форме идеальные прямоугольные колебания. |
|
Ряд по |
Уолша широко применяется в задачах математического и фи- |
зического моделирования СТК и измерительных систем (устройств), поскольку |
|
характер зуетсяббыстрой сходимостью (существенно лучшей, например, чем |
|
рядБФурьефункциям) позволяет избежать во многих случаях аппроксимации кусочнонепрерывных функций возникновения игольчатых выбросов в точках их разры-
ва.
Известны разные способы определения функций Уолша. Наиболее распространенный из них основан на взаимосвязи функций Уолша с функциями
Радемахера. |
|
|
|
|
|
Функции Радемахера аналитически задаются в виде |
|
||||
r ( ) sign sin 2k |
, |
k |
|
, |
(2.43) |
1, |
|||||
k |
|
|
|
|
|
где k – порядок функции; t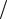 T безразмерный аргумент (безразмерное время), нормированный относительно произвольного (заданного) интервала
T безразмерный аргумент (безразмерное время), нормированный относительно произвольного (заданного) интервала
1, x 0,
длительностью T ; sign x
1, x 0.
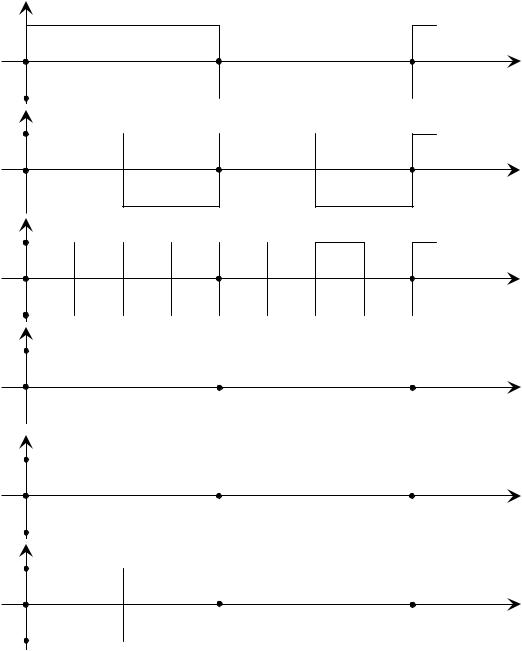
Функции Радемахера являются периодическими, образуют ортонормированную с единичным весом на отрезке 0, 1 систему функций, которая однако
не является полной. Объясняется это тем, что функции rk ( ) являются нечетными относительно точки 0,5 (рисунок 2.3, а-в) и могут быть использованы для аппроксимации только нечетных функций. По этой причине переходят к
функциям Уолша (рисунок 2.3, г-е). |
|
|
|
|
|
|
|
|
И |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Способ задания функций Уолша через функции Радемахера основан на |
||||||||||||||
том, что каждая функция wal(w, ) Уолша порядка w, |
входящаяРв систему из |
|||||||||||||
N 2n |
функций, является произведением функций Радемахера (в соответст- |
|||||||||||||
вующих степенях) первых n порядков: |
|
|
Б |
|
|
|
|
|
|
|
||||
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
k 1 , |
w 0, |
Уn |
(2.44) |
|||||||
|
|
|
||||||||||||
|
|
wal(w, ) rk k |
|
|
2 1, |
|
||||||||
|
|
k 1 |
а |
Г |
|
|
a 2k |
a 2n |
||||||
где a , a |
|
|
|
|
|
|
|
|
||||||
коэффициенты, представляющие число w a 20 a21 |
||||||||||||||
k |
k 1 |
|
|
|
|
|
|
0 |
|
1 |
|
k |
n |
|
в n 1 -разрядной двоичной системе исчисления. Основываясь на алгоритме
(2.44), можно, в |
частности, |
е |
|
wal(0, ) r0 |
( ) r0 |
( ) r0 |
( ), |
||||||
установить, что |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
wal(3, ) r0( ) r1( ) r0( ) и wal(6, ) r1 |
( ) r0( ) r1( ). |
|
|
||||||||||
|
1 |
|
2 |
3 |
т |
к1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
r1( )
1.0 
0
0.5 |
1.0 |
-1.0 |
|
|
|
|
r2( ) |
а |
|||
1.0 |
|
|
|
|
|
|
|
|
|
0
0.5 |
1.0 |
-1.0 
r3( ) |
|
|
|
|
б |
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
||||
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
||||
-1.0 |
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
У |
Р |
|
||||||||
wal(0, ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|||||
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0.5 |
|
|
а |
|
|
1.0 |
|
|
|
|
|
|
|
|||||
wal(1, ) |
|
|
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.0 |
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
wal(2, ) |
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.0 |
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|||||||
-1.0 |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рисунок 2.3 – Функц |
Радемахера (а-в) и Уолша (г-е) |
|
|
|
|
|
|
|
||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Функции |
Уолшаобладают следующими свойствами: |
|
|
|
|
|
|
|
||||||||||||||||||
являются периодическими с периодом, равным единице; |
|
|
|
|
|
|
|
|||||||||||||||||||
функц |
четных порядков wal 2 j, |
являются четными, а нечетных |
||||||||||||||||||||||||
wal 2 j 1, |
нечетными относительно точки |
0,5 (см. рисунок 2.3, |
г-е), |
|||||||||||||||||||||||
вследствиеБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
2 |
|
|
|
||
чего по аналогии с тригонометрическими функциями |
k |
|
t |
их |
||||||||||||||||||||||
T |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
||
иногда |
обозначают |
соответственно |
|
wal(2j, ) cal( j, |
) |
|
|
и |
||||||||||||||||||
wal(2j 1, ) sal( j, );
имеют |
свойство |
мультипликативности |
wal(k, ) wal(i, ) |
wal(k i, |
), т.е. перемножение двух функций Уолша дает новую функцию; |
||
обладают свойством симметрии относительно порядка и аргумента (времени), с учетом которого предыдущее свойство мультипликативности можно
представить также в виде wal(i, 1 ) wal(i, 2 ) wal(i, |
1 2 ); |
||||||||||||
образуют полную систему функций, ортонормированную с единичным |
|||||||||||||
весом на отрезке 0, 1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
в соответствии с условиями теоремы разложения в обобщенный ряд Фу- |
|||||||||||||
рье представляют моделируемую функцию |
f( ) (нормированного аргумента) |
||||||||||||
на отрезке 0, 1 рядом (по функциям Уолша) |
|
|
|
|
И |
||||||||
|
|
|
|
|
|
|
|
|
|
У |
Р(2.45) |
||
f( ) Cnwal(n, |
), |
|
|
||||||||||
1 |
|
|
n 0 |
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
где Cn f( )wal(n, )d , |
|
( t/T). |
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
Функции Уолша периодичны, поэтому ряд (2.45) в основном используют |
|||||||||||||
для аппроксимации периодических функций |
f( ) f( 1). При нахождении |
||||||||||||
спектральных коэффициентов Cn |
(по |
Уолша |
|
|
|
|
|
||||||
н логии с рядом Фурье) операцию ин- |
|||||||||||||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
тегрирования можно выполнять не толь на отрезке 0, 1 , но на любом отрез- |
|||||||||||||
|
|
|
|
е |
являются базисом спектрального |
||||||||
ке единичной длительности. Функции |
|
||||||||||||
(негармонического) представл ния сигналов. |
|
|
|
|
|
|
|||||||
2.8 Моделирование сигналов на основе преобразования Фурье |
|||||||||||||
Ортогональные |
во |
|
|
|
|
|
|
|
|
|
|
||
|
|
емы базовых функций описывают исследуемые сиг- |
|||||||||||
сис |
временнойт |
области). Наряду с этим в задачах модели- |
|||||||||||
налы на оси времени ( |
|
||||||||||||
л |
|
спользуют их представление в частотной области и на |
|||||||||||
рования СТК ш роко |
|||||||||||||
комплексной п оскости. Описание сигналов в частотной области осуществляют с помощью разования Фурье. Большинство современных программ математического моделирования искажений сигналов реализуют классическое (непрерывное) разование Фурье или его последующее развитие в вариантах
дискретного быстрого преобразований. |
|
|
||
|
преоб |
|
|
|
Как звестно, прямое преобразование Фурье ставит во взаимно однознач- |
||||
и |
f(t ) S( ) исходному сигналу |
f(t ) |
(функции времени) |
|
ное соответствие |
||||
спектральную плотность (спектральную характеристику) |
|
|||
Б |
|
|
|
|
|
|
S( ) f(t )e j tdt, |
|
(2.46) |
|
|
|
|
|
являющуюся в общем случае комплекснозначной функцией частоты . Обратный переход от спектральной плотности S( ) к сигналу f(t ) выполняется с помощью обратного преобразования Фурье:
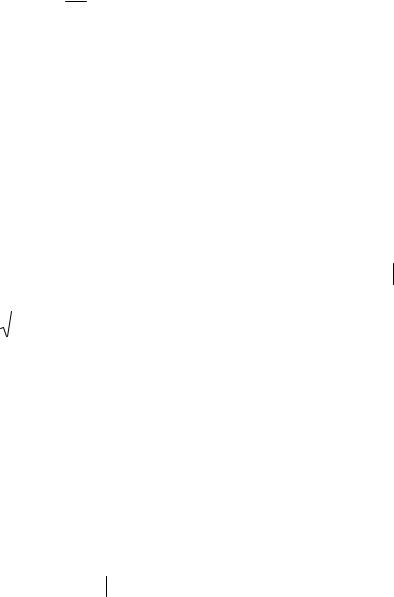
f(t ) 1 S( )ej td . (2.47)
2
Для представления интегралом (2.46) Фурье функция (сигнал) f(t ) должна удовлетворять на бесконечном интервале , тем же условиям
Дирихле и абсолютной интегрируемости, что и в случае ряда Фурье (см. подразд. 2.4). Отметим при этом, что условию абсолютной интегрируемости отвечают непериодические финитные сигналы и непериодические бесконечно про-
тяженные сигналы, описываемые функциями f(t ) с быстро спадающими “хво- |
|
стами”. |
Р |
|
|
По аналогии со спектральными коэффициентами Cn ряда Фурье (см. (2.20)-(2.22)) спектральную плотность S( ) можно представить в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S( ) |
f(t )cos tdt j f(t )sin tdt A( |
) jB( |
|
У |
||||||||||
) S( )ej ( ), (2.48) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
B( ) |
|
|
|
|
где |
|
S( ) |
|
|
A2( ) B2( ) |
; |
( ) arctg |
. |
|
|
||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( ) |
|
|
|
Модуль |
|
|
S( ) |
спектральной |
плотности |
являетсяГчетной, а аргумент |
||||||||
( ) нечетной функциями частоты. Они описывают непрерывные матема-
|
|
|
|
|
к |
мплитудный и фазовый соответ- |
||||||
тические спектры непериодического сигн : |
||||||||||||
|
|
|
|
|
е |
|
|
|
|
|||
ственно. Значение S(0) |
|
f (t)dt сп |
|
тральнойлаплотности S( ) численно рав- |
||||||||
но площади (с учетом знака) под кривой f(t ) |
сигнала. |
|||||||||||
|
2 |
соо |
|
(2.48), |
0 |
|||||||
Основываясь на |
|
|
ношении |
обратное преобразование (2.47) |
||||||||
представляют также в ф рме |
тj ( ) |
|
|
|
|
|
|
|
||||
и |
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
j t |
|
1 |
|
|
|||
f(t ) |
|
|
|
S( |
)e |
e |
|
d |
|
|
S( ) |
cos( t ( ))d , (2.49) |
|
|
|
|
|
|
|
|
|
|
|
|
|
которая широко пр меняется в практике моделирования, особенно при исполь- |
||
зовании численных методов. |
|
|
Рассмотримлнепериодический финитный сигнал fT (t ) произвольной |
||
формы дл тельностью T . Периодическим повторением с периодом T обра- |
||
б |
f(t ). Очевидно, |
сигнал |
зуем соответствующий ему периодический сигнал |
||
fT (t ) иописывается спектральной плотностью S( ) (2.46), сигнал f(t ) |
спек- |
|
тральными коэффициентами Cn (2.20). Сравнивая эти выражения, устанавлива- |
|
Б |
|
ем: |
|
S(n 1 )/T Cn . |
(2.50) |
Последнее означает, что непрерывный амплитудный спектр непериодического сигнала и огибающая дискретного амплитудного спектра соответствующего ему периодического сигнала совпадают по форме. Соотношение (2.50) рекомендуется использовать при моделировании. Оно позволяет, зная выражение

для спектральных коэффициентов, сразу перейти к выражению для спектральной плотности и, наоборот, от спектральной плотности к спектральным коэффициентам.
Нахождение спектральной плотности S( ) непосредственно по выражению (2.46) требует во многих случаях очень хорошей математической подготовки и весьма значительных затрат времени, без чего можно успешно обойтись, если использовать известные свойства преобразования Фурье. Анализ задач, решаемых при моделировании, показывает, что в основном применяются следующие свойства.
|
|
|
Свойство |
линейности. |
Если |
|
fi ( t ) Si |
( ) |
( i 1, N ) , |
то |
||||||||||
|
|
|
N |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
И |
|
|
f (t) Ai fi(t) S( ) AiSi( ) ( Ai |
|
– постоянные коэффициенты), т.е. ли- |
||||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
У |
Р |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нейной суперпозиции сигналов |
fi(t ) соответствует линейная суперпозиция их |
|||||||||||||||||||
спектральных плотностей |
|
|
|
|
|
Г |
|
|
|
|||||||||||
Si( ). Доказательство свойства выполняется под- |
||||||||||||||||||||
становкой f(t ) в интеграл (2.46) Фурье. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Свойство |
сдвига |
по |
времени. |
Если |
f1 ( t ) S1( ) , |
то |
|||||||||||
f |
|
(t ) f |
|
(t t |
|
) S |
|
( ) S ( |
|
на |
0 |
|
|
|
|
|||||
|
2 |
|
|
1 |
|
0 |
|
|
2 |
|
1 |
|
|
f1(t )Бизменяет только его фазовый |
||||||
сдвиг |
по |
времени исходного |
сигнала |
|
||||||||||||||||
спектр: начальная фаза ( ) каждой спе тр льной компоненты получает от- |
|||
|
е |
угол t , прямо пропорциональ- |
|
рицательное (положительное) приращ ние |
|||
т |
|
|
|
ный частоте и времени t0. Доказаткльство свойства выполняют по следую- |
|||
щей схеме: рассматривают произвольный финитный сигнал |
f1(t ), заданный на |
||
о |
|
на отрезке t1 t0 , |
t2 t0 , подверга- |
отрезке t1, t2 , переходят к сигналу f2(t ) |
|||
ют последний преобраз ванию (2.46), используя при интегрировании замену
t |
t0 переменной. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
л |
|
масштаба по времени. Если f1(t ) S1( ), то |
|||||
|
|
Свойство зменен я |
|||||||||||
|
|
|
|
|
|
и |
1 |
|
|
|
|||
f |
|
(t ) f |
|
(nt ) S |
|
( ) |
|
S |
|
|
, т.е. растяжению (n 1) или сжатию (n 1) |
||
|
|
|
n |
|
|||||||||
|
2 |
|
1 |
|
|
|
2 |
|
1 |
n |
|||
|
|
и |
гнала по времени в n раз соответствует такое же по величине сжа- |
||||||||||
исходного с |
|
||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
||
тие (растяжениеб) его спектральной плотности по частоте при одновременном |
|||||||||||||
увел чен |
|
|
(уменьшении) амплитуд спектральных компонент в n раз. Доказа- |
||||||||||
тельство свойства выполняют по следующей схеме: рассматривают произволь-
ный финитный сигнал |
f1(t ), заданный на отрезке 0, t1 , переходят к сигналу |
|||||
f2(t ) на отрезке |
0, t1 |
/ n , который подставляют в интеграл (2.46) с после- |
||||
дующей заменой t / n в нем переменной. |
|
|||||
Свойство |
смещения |
спектра сигнала. Если f1(t ) S1( ), |
то |
|||
f2 t f1 t cos 0t 0 |
S2 |
|
1 |
e j 0 S1 0 e j 0 S1 0 , |
т.е. |
|
|
||||||
|
|
|
2 |
|
|
|
умножение исходного сигнала f1 t на гармоническое колебание с частотой 0 приводит к расщеплению его спектра на две составляющие, смещаемые по частоте на 0 . Доказательство свойства выполняется подстановкой f2 t в интеграл (2.46) и представлением функции cos 0t 0 по формуле Эйлера.
|
|
Свойство |
дифференцирования |
сигнала. Если f1(t ) S1( ), то |
|||
|
|
(t ) f ' (t ) S |
|
|
j |
|
|
f |
|
|
|
|
, т.е. операция дифференцирова- |
||
2 |
2 |
( ) j S ( ) S ( )e 2 |
|||||
|
1 |
1 |
1 |
|
|
||
ния приводит к относительному уменьшению (увеличению) амплитуд низкочастотных (высокочастотных) спектральных компонент исходногоРсигнала и
дополнительному (опережающему) приращению их начальных фаз на угол
|
|
|
И |
0 |
|
|
. Доказательство свойства осуществляется подстановкой f2(t ) в инте- |
|
2 |
|
|
грал (2.46) и вычислением последнего с помощью метода интегрирования по
частям. Как известно, физическую реализацию математической операции диф- |
||||||||||||||
ференцирования сигнала (функции) |
|
|
|
|
|
|
|
|
Г |
|||||
f1(t ) с определенной погрешностью вы- |
||||||||||||||
полняет простейшая дифференцирующая C R — цепь,Упричем величина по- |
||||||||||||||
грешности тем меньше, чем меньше постоянная RC этой цепи. |
||||||||||||||
Свойство |
интегрирования |
сигнала. |
|
Если |
f1(t ) S1( ), то |
|||||||||
t |
|
|
|
|
|
|
а |
|
|
|||||
f2(t ) f1(t )dt S2( ) |
1 |
|
|
|
S ( ) |
|
j |
|
Б |
|
||||
|
S1 |
( ) |
1 |
|
|
e |
2 , т.е. операция интегрирова- |
|||||||
|
|
|
|
|||||||||||
|
|
j |
е |
|
|
|
|
|
|
|||||
ния приводит к относительному ув лич нию (уменьшению) амплитуд низко- |
||||||||||||||
частотных (высокочастотных) сп |
ктральных |
компонент исходного сигнала и |
||||||||||||
дополнительному (запаздывающ му) приращению их начальных фаз на угол
0 |
|
|
|
|
|
|
|
|
свойс |
|
|
|
|
|
|
|
|
|
|
||||||
|
. Доказательство |
|
|
|
ва наиболее просто выполняется представле- |
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
f |
|
имеют |
f (t ) |
f ' (t ) |
|
|
|
|
|
0 1 |
|
|
||||
нием сигнала |
|
(t ) в в де |
|
и последующим использованием свой- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1т2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
л |
|
|
|
Свойство интегрирования применимо только к тем |
||||||||||||
ства дифференцирован я. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сигналам, |
которые |
|
|
|
|
нулевую (с учетом знака) площадь lim S ( ) 0 . |
|||||||||||||||||||
|
|
и |
|
|
|
|
|
математической операции |
интегрирования |
|
сигнала |
||||||||||||||
Физическую реализацию |
|
|
|||||||||||||||||||||||
(функц |
|
|
) |
f1(t ) с погрешностью выполняет простейшая интегрирующая |
|||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
R C — цепь, причем величина погрешности тем меньше, чем больше постоян- |
|||||||||||||||||||||||||
ная RC этой цепи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Свойство произведения сигналов. Если f1(t ) S1( ) и f2(t ) S2( ), |
|||||||||||||||||||||||
то |
|
произведение |
|
|
f(t ) f |
(t ) f |
|
(t ) S( ) |
|
|
S |
( x)S |
|
( x)dx |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
2 1 |
|
2 |
|
|
|
1 |
S |
( x)S |
|
( x)dx, |
т.е. произведению исходных сигналов соответствует |
|||||||||||||||||||
|
|
||||||||||||||||||||||||
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
свертка их спектральных плотностей. Доказательство свойства выполняют по
следующей схеме: подставляют сигнал f(t ) в интеграл (2.46), представляют сигнал f2(t ) f1(t ) обратным преобразованием (2.47) Фурье, переходят к
двойному интегралу и заменяют порядок интегрирования.
Из свойства произведения сигналов при 0 вытекает важ-
ное |
для |
практики моделирования |
следствие: |
|
f1(t) f2(t)dt S(0) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
S1(x) S2( x)dx |
|
|
|
S1( ) S |
2*( )d |
|
|
|
S1*( ) S2 |
( )d , |
где |
||||
2 |
|
2 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
||
S1*( ) S2*( ) функция, |
комплексно-сопряженная |
|
функции |
(спектральной |
|||||||||||||
плотности) |
S1 ( ) S2 ( ) . |
|
|
|
|
|
|
|
|
|
И |
|
|||||
Очевидно, следствие определяет энергию взаимо- |
|||||||||||||||||
действия сигналов f1(t ) |
и |
f |
|
|
|
|
|
|
У |
|
|
||||||
2(t ) через их спектральные плотности S1( ) и |
|||||||||||||||||
S2( ). |
|
|
|
|
|
|
|
|
Г |
и S2( ) f2 |
(t ), |
||||||
|
|
Свойство произведения спектров. |
|
||||||||||||||
|
|
Если S1( ) f1(t ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Б |
f1(t ) f2( )d , т.е. |
||||||
то S( ) S1( ) S2( ) f(t ) f1( )f2(t )d |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
произведению спектральных плотностей исходных сигналов соответствует свертка этих сигналов. Доказательство осуществляется аналогично предыду-
щему свойству. Из свойства произведения спектров вытекает известный метод |
|||
|
|
е |
|
моделирования по формуле Дюам ля. |
|
||
Свойство взаимозаменя мостиквр мени и частоты. Если f(t ) S( ), |
|||
т |
повторяющему по форме спек- |
||
то S(t ) F( ) 2 f( ), |
|
.е. сигналу S(t ), |
|
о |
|
f(t ), соответствует спектраль- |
|
тральную плотность S( ) |
исходного сигнала |
||
ная плотность F( ) 2 f( ), пов оряющая по форме исходный сигнал. Свой-
ство справедливо для с гнала, описываемого четной функцией |
f(t ). Его спек- |
||||||||||||||||||||
тральная |
|
п отность |
S( ) также представляет собой вещественную четную |
||||||||||||||||||
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
||||
функцию. Поэтомуиобратное преобразование Фурье можно представить в виде |
|||||||||||||||||||||
|
|
1 |
|
|
j t |
|
|
|
|
|
|
|
|
||||||||
f t |
|
|
|
|
Sлe |
d . Формально выполняя в последнем интеграле замену |
|||||||||||||||
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F( ) |
||||
на t |
|
t на , приходим к выражению для спектральной плотности |
|||||||||||||||||||
сигналаиS(t ). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
БРавенство Парсеваля. Если f (t ) S( ), то |
|
|
|
||||||||||||||||||
Э |
f 2 ( t |
)dt |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
S( ) |
|
2 d |
|
|
|
S( ) |
|
2 d . Равенство Парсеваля является частным случа- |
||||||||||
|
|
|
|
||||||||||||||||||
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
ем f1(t ) f2(t ) f(t ) следствия из свойства произведения сигналов. Оно
определяет энергию непериодического сигнала f(t ) через спектральную плот-
ность S( )2 энергии, показывает, что последняя не зависит от начальных фаз
спектральных компонент. Равенство Парсеваля широко применяется в СТК при моделировании энергетических характеристик сигналов, включая определение уровней внеполосных излучений.
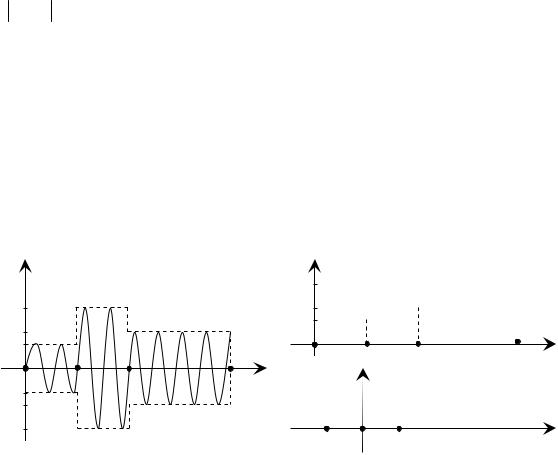
В качестве примера использования свойств преобразования Фурье най-
дем |
|
|
спектральную |
|
плотность |
|
S( ) |
|
|
финитного |
|
радиосигнала |
||||||||||||||||||||||||||
f(t ) f1(t )cos( 0t 0 |
) с |
|
|
|
частотой |
|
0 |
|
заполнения, |
начальной |
фазой |
|||||||||||||||||||||||||||
0 |
|
и огибающей |
|
f1(t ), составленной из трех идеальных прямоугольных |
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||
импульсов разной длительности и амплитуды (рисунок 2.4, а, б). |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f(t ) |
|
|
|
|
|
|
|
|
|
|
4A |
|
|
|
f1(t ) |
|
|
|
|
|
И |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
б |
|
12 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г6 |
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
f |
0(t ) |
|
|
|
|
|
|
|
||||
-A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
||||
-4A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
в |
|
|
|
t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Рисунок 2.4 – Определ |
|
сп |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
тральной плотности |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
непериодического радиосигнала f(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для упрощения решения задачи введем в рассмотрение элементарный |
||||||||||||||||||||||||||||||||||||||
сигнал f0(t ) (назовем |
|
баз вым) (рисунок 2.4, в), с помощью которого мож- |
||||||||||||||||||||||||||||||||||||
но описать огибающую |
f1(tт). Его спектральная плотность, найденная с помо- |
|||||||||||||||||||||||||||||||||||||
щью прямого преобразованегоя Фурье (2.46), равна S0( ) 2Asin / . Оче- |
||||||||||||||||||||||||||||||||||||||
видно, |
|
что f1(t) f0 |
и(t ) 4 f0 |
(1 (t 4 )) 2 f0 |
( |
1 |
|
(t 9 )) . Поэтому |
воспользуемся |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
свойствами линейностил, сдвига по времени и изменения масштаба, с помощью |
||||||||||||||||||||||||||||||||||||||
которых |
|
сразу |
определяем |
|
спектральную |
|
|
плотность |
|
огибающей: |
||||||||||||||||||||||||||||
S1( ) |
|
|
|
|
бj |
8S0(2 )e |
j4 |
6S0 |
(3 )e |
j9 |
. |
Зная последнюю, |
|
с помо- |
||||||||||||||||||||||||
S0( |
)e |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
щью свойстваисмещения спектра переходим к искомой спектральной плотности |
||||||||||||||||||||||||||||||||||||||
S(Б) |
1 |
|
j |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
e |
|
2 S ( |
0 |
) e |
|
2 S ( |
0 |
) |
. Далее остается выполнить оконча- |
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельные преобразования с учетом выражения для спектральной плотности
S0( ).

2.9 Дельта-функция и её свойства
В теории информационных систем, включая СТК, особое место принадлежит -функции, на базе которой, в частности, построены дискретное преобразование Фурье и Z–преобразование. Совместное применение преобразования Фурье и -функции позволяет во многих случаях обойти ограничения, связанные с выполнением условия абсолютной интегрируемости.
-функцию, называемую также единичным импульсом, импульсной
функцией и функцией Дирака, можно ввести предельным переходом под зна- |
|||||||||||||||||||||||||
ком многих функций, например, в виде |
|
|
|
|
|
|
|
|
|
Р |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
t t |
0 |
, |
|
||||
|
|
(t t |
|
) lim f |
|
(t) lim f |
|
(t) lim |
f |
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
1 |
2 |
3 |
(t) |
t t |
|
|
, (2.51) |
|||||||||||||||
|
|
|
|
t1 0 |
|
a 0 |
|
fm |
|
|
|
0, |
0 |
||||||||||||
|
|
|
|
t |
|
|
|
|
|
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 t1 , |
|
0 t1 |
|
2 , t0 t1 |
|
|
|
|
|
|
1 |
|
|
(t t0 )2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
2a2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где f1 (t) 0, |
|
t0 |
t1 |
2, |
t0 t1 |
2 , |
Иe |
|
|
|
|
; |
|||||||||||||
|
f2 |
(t ) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|||
f3 |
(t ) |
sin2 fm(t t0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(t t0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
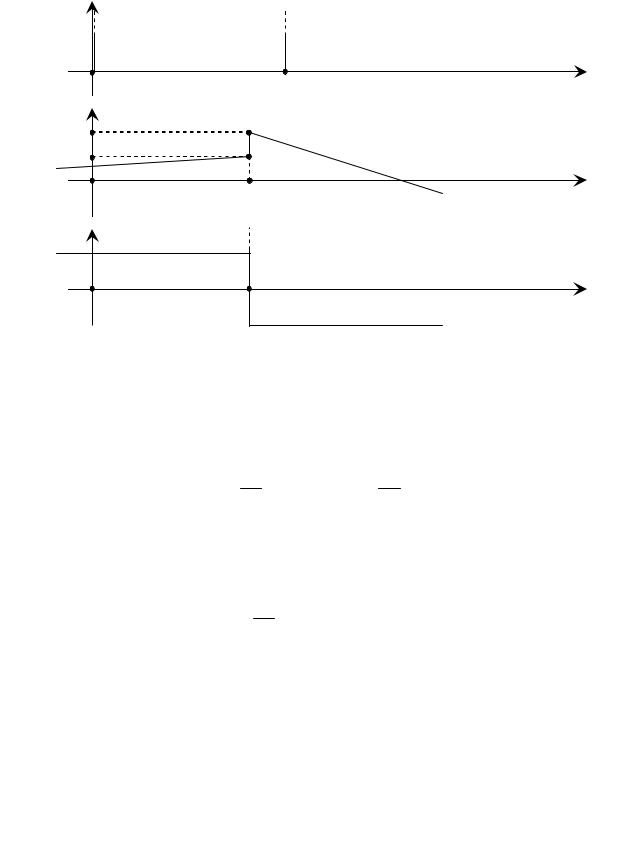
Как следует из выражения (2.51), она существует в единственной точке t t0 |
||||||||||||||||||
(при |
t0 0 |
|
(t t0 ) (t )) |
( |
|
|
|
2.5,Ба), обладает размерностью |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
рисунок |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
||||
(t t0) c 1 |
и площадью |
(t t0 )dtа1. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
||
|
Важное значение для прим н ния -функции имеет её фильтрующее |
|||||||||||||||||
(стробирующее) свойство |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(t t0 ) f (t)dt f (t0 ) (t t0 )dt f (t0) . |
(2.52) |
|||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Очевидно, спектральная плотность S ( ) -функции равна |
|
||||||||||||||||
|
|
|
являясь |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
б |
S |
( ) |
(t t0 )e j tdt e j t0 . |
(2.53) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
безразмерным, |
|
равен |
|
S ( ) |
|
1. Последнее в соответствии |
||||||||||
Её модуль, |
|
|
|
|
|
|||||||||||||
с равенством Парсеваля означает, |
|
что энергия -функции равна |
Э . При |
|||||||||||||||
Б |
|
|
|
|
|
|
|
|
S |
( ) является вещественной функцией: все |
||||||||
t0 0 |
спектральная плотность |
|||||||||||||||||
гармонические составляющие единичного импульса, суммируясь при нулевых начальных фазах, образуют в момент времени t0 0 пик бесконечно большой величины.
(t t0 ) |
|
|
|
|
|
|
|
|
|
|
|
(t t0) |
|
|
|
|
|
|
|
|
|
|
|
||
(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(t ) |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
f11(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
t |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рисунок 2.5 – - функция и её применение при дифференцировании |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||
Применяя |
к |
спектральной |
плотности S |
( ) обратное преобразование |
|||||||||||||||||||||
Фурье, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
) 1 |
|
1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
(t t |
|
|
|
|
e j (t t0 )d . |
|
(2.54) |
|||||||||||||||
|
|
|
|
|
ej (t t0 )d |
|
|
||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
2 е |
|
2 |
|
|
|
|
|
|
||||||||
Выражение (2.54) м |
|
|
|
|
рассма ривать как ещё одно определение функ- |
||||||||||||||||||||
ции (t t0 ) (через част тную |
бласть). Формально заменяя в нем время t(t0 ) |
||||||||||||||||||||||||
на частоту ( |
|
), |
|
|
|
|
|
|
т |
|
|
|
|
|
), приходим к определению |
||||||||||
|
а част ту ( |
|
|
) на время t(t |
|
||||||||||||||||||||
|
0 |
|
|
жно |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
( |
|
|
) |
1 |
e |
( )t |
dt |
|
|
|
|
|
|
|
|
|
(2.55) |
|||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
и |
|
|
как и функция (t t |
|
) |
|
|
|
||||||||||||||
-функции на оси частот, которая, |
0 |
на оси времени, |
|||||||||||||||||||||||
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
применяется при моделировании СТК. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В практ ке математического моделирования широко используются сиг- |
|||||||||||||||||||||||||
налы, иописываемые кусочно-непрерывными функциями. Учитывая это, рас- |
|||||||||||||||||||||||||
смотрим функцию |
f1(t) , |
|
|
имеющую при |
t |
|
|
t0 |
разрыв первого рода (рису- |
||||||||||||||||
нокБ2.5, б). С позиции классического математического анализа она является |
|||||||||||||||||||||||||
дифференцируемой при всех t ( ; ), |
за исключением точки t |
t0 . Введем |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
далее функцию |
|
f11(t ) f1' |
(t ). Тогда |
f1(t ) f11(t )dt. С учетом последнего и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

свойств -функции вытекает, что функция f1(t ) в точке t t0 разрыва первого рода имеет производную (рисунок 2.5, в)
f11(t0 ) ( A2 A1 ) (t t0 ), |
(2.56) |
где A |
lim |
f (t); |
A |
lim |
f (t). |
1 |
t t0 0 |
1 |
2 |
t t0 0 |
1 |
Таким образом, дополнительное использование свойства (2.56) распространяет обычные правила дифференцирования также на кусочно-непрерывные функции с разрывами первого рода.
|
|
Р |
2.10 Совместное применение свойств преобразования Фурье |
||
и дельта-функции при моделировании сигналов |
И |
|
Важной задачей при синтезе СТК является правильный выбор формы |
||
У |
|
|
сигнала, которая определяет скорость уменьшения с ростом частоты амплитуд его спектральных компонент и, значит, эффективную ширину спектра. Оказы-
вается, скорость убывания спектра зависит от порядка |
n производной f (n )(t ) |
|||||||||
(функции f(t ), |
|
|
|
|
|
|
Б |
|
|
|
описывающей сигнал), в которой возникает -функция. Для |
||||||||||
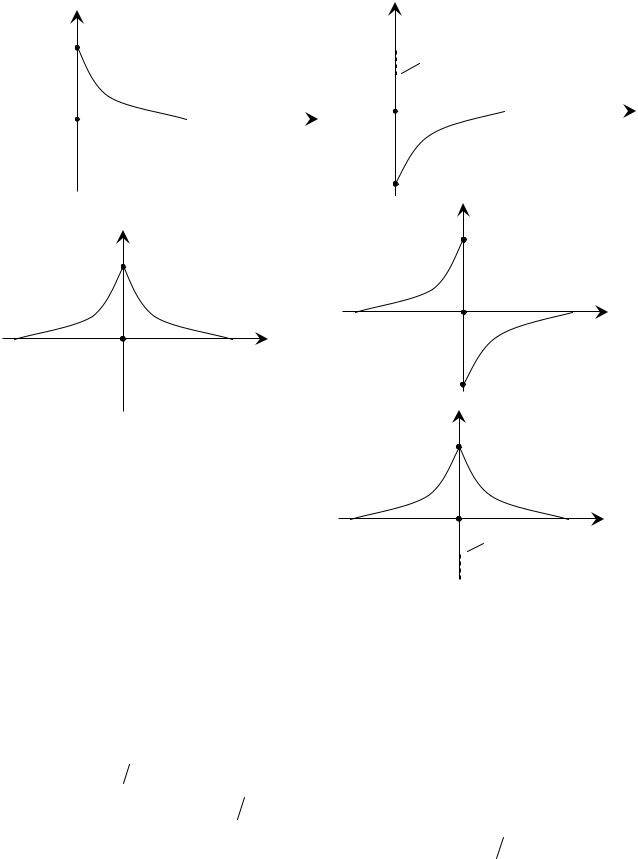
выяснения этой закономерности рассмотрим функциюГf (t ) и её производную |
||||||||||
f11(t ) (рисунок 2.6, а, б): |
|
|
|
|
|
1 |
|
|||
|
|
к |
|
|
|
|
||||
|
|
|
|
|
|
t |
|
|
||
|
t |
|
|
|
|
A (t) A e |
, |
t 0, |
||
Ae |
, 0, |
t 0, |
f11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f1(t) |
|
|
|
(t) |
|
|
|
|
||
0, |
t 0, |
|
е |
а0, t 0. |
|
|
|
|||
|
|
|
т |
|
|
|
|
|
функции f11(t ) рав- |
|
Нетрудно установить, что спектральная плотность S11( ) |
||||||||||
на S11( ) j A |
( j ). Очевидно, S11(0) 0. Это позволяет, воспользовав- |
||||||||||||||||||||||
шись |
свойством |
|
интегрирования, |
сразу перейти к спектральной плотности |
|||||||||||||||||||
S1( ) функции |
f1(t ): S1( ) A ( j ). |
|
|
Отсюда |
|
вытекает, |
что |
||||||||||||||||
lim |
|
S ( ) |
|
|
A |
~ |
1 |
, |
т.е. амплитудный спектр на высоких частотах убывает по |
||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
закону 1 . |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
f2(t ), её первую |
f21(t ) |
|
|
f22(t ) |
||||||||||
|
|
Рассмотрим да ее функцию |
и вторую |
||||||||||||||||||||
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
про зводные (рисунок 2.6, в-д): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
бAe t , 0, t 0, |
|
A |
|
t |
, t |
|
0, |
|
||||||||||||
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||
|
|
(t) |
|
t |
|
f21(t) |
|
|
|
|
t |
|
|
|
|
|
|||||||
и |
|
Ae , |
t 0, |
A e , t 0. |
|
|
|||||||||||||||||
Б |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
t |
, t 0, |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2A (t) A e |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f22 (t) |
|
|
|
|
|
|
|
|
|
|
|
A 2e t , t 0.
f1(t ) |
|
|
|
|
|
|
|
|
|
|
f11(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A (t ) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
а |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||
f2(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
21(t ) |
|
|
A |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И t |
||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
г |
|
|
|
|
|
|||||||
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
а |
f22 |
(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
т |
|
|
|
|
|
|
0 |
|
|
|
2 A ( t ) |
|
t |
||||||||||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2.6 – Временные свойства сигналов, описываемых |
|
|
|||||||||||||||||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
кусочно-непрерывными функциями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б |
|
иf ( t ) |
2 |
f |
|
( t ) |
2 A ( t |
) . |
|
|
Поэтому |
с |
учетом |
||||||||||||||||
Очевидно, |
|
2 |
|
|
|||||||||||||||||||||||||
и |
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
( ) 2 S 2 ( ) |
2 A |
||||||||||||||
свойств прео разования Фурье и -функции S 22 |
|||||||||||||||||||||||||||||
( S 2 ( ) f2 |
(t), S 21 ( ) f21 (t), |
S 22 ( ) |
f22 |
(t) ). |
Поскольку |
||||||||||||||||||||||||
S 22 ( 0 ) S 21 |
( 0 ) 0 , |
то |
на |
основании |
|
свойства |
|
|
интегрирования |
||||||||||||||||||||
S2( ) S22( ) |
( j ) . Подставляя в последнее соотношение выражение для |
||||||||||||||||||||||||||||
SБ( ), имеем |
S |
2 |
( ) 2A ( 2 2 ). |
|
Отсюда |
lim |
|
S |
|
|
( ) |
|
|
2A |
~ |
1 |
|
, т.е. |
|||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
амплитудный спектр убывает на высоких частотах по закону 1 2 . |
|
|
|
|
|
||||||||||||||||||||||||
Проведенный анализ показывает следующее. Сигнал, описываемый |
|||||||||||||||||||||||||||||
функцией f(t ), в первой производной f ' (t ) которой возникает |
-функция, |
||||||||||||||||||||||||||||
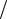
имеет амплитудный спектр, убывающий по закону 1 . Сигнал, представляемый функцией, во второй производной которой появляется -функция, имеет убывающий по закону 1
. Сигнал, представляемый функцией, во второй производной которой появляется -функция, имеет убывающий по закону 1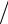 2 амплитудный спектр. Ранее установлено, что сиг-
2 амплитудный спектр. Ранее установлено, что сиг-
нал, описываемый функцией f(t ) f (0)(t ) (t t0 ), имеет равномерный спектр (по-другому, убывающий по закону 1 0 ). Обобщая полученные результаты, устанавливаем общую закономерность: сигнал, представляемый функцией f(t ), в n-й производной f (n )(t ) которой возникает -функция, об-
0 ). Обобщая полученные результаты, устанавливаем общую закономерность: сигнал, представляемый функцией f(t ), в n-й производной f (n )(t ) которой возникает -функция, об-
ция, то это свидетельствует о наличии в сигнале (его производныхР) нескольких, по крайней мере двух -функций. Так, периодическая пульсация амплитудного
ладает амплитудным спектром, убывающим на высоких частотах по закону
1 n . Если одновременно с убыванием спектра наблюдается также его пульса-
n . Если одновременно с убыванием спектра наблюдается также его пульса-
спектра с неубывающими максимумами может возникать только в результате
интерференции спектров нескольких -функций. Амплитудный спектр идеаль- |
||
|
И |
|
ного прямоугольного импульса, пульсирующий с убывающими по закону 1 |
||
|
У |
|
максимумами, результат интерференции спектров двух ступенчатых скачков. |
||
В соответствии с общей закономерностью наибольшуюГ |
скорость убыва- |
|
ния амплитудного спектра имеет импульс |
, производная любого порядка |
|
которого является непрерывной фун |
. ОднакоБон обладает бесконечной |
|
длительностью, вследствие чего на пр |
|
ти е не используется. Вместо него в |
|
СТК широко применяют финитный cos2 |
-импульс, примерно повторяющий по |
||
|
|
Гаусса |
|
свойствам импульс Гаусса. |
кцией |
||
В практике математического мод лирования СТК часто используются |
|||
сигналы, которые описываю сяефункциями, не удовлетворяющими условию |
|||
абсолютной интегрируем с и. Совместное применение свойств преобразования |
||||||||||||||||||
Фурье и -функции во мн гих случаях позволяет обойти это ограничение. |
||||||||||||||||||
Рассмотр м |
|
гармтническое |
колебание |
f(t ) Acos( 0t 0 ), |
||||||||||||||
t . |
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
применяя к нему прямое преобразование Фурье (2.46) |
||||||||||||||
и используя опреде ен е (2.55) |
-функции, можно получить следующее выра- |
|||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
жение для его спектра ьной плотности: |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
S( |
) A e |
j 0 |
( |
0 |
) e |
j 0 |
( |
0 |
) . |
(2.57) |
||||
|
|
|
|
|
|
|
||||||||||||
|
|
Формально |
|
|
|
|
|
|
|
|
|
|
|
|||||
Постоянное напряжение (ток) f0(t ) |
|
lim |
Acos( 0t 0 ) A. Вы- |
|||||||||||||||
|
б |
|
|
|
|
|
|
|
|
0 0, 0 0 |
|
|
|
|
||||
полняяив выражении (2.57) предельные переходы 0 |
0 |
и 0 0, устанав- |
||||||||||||||||
ливаем, что сигналу f0(t ) соответствует спектральная плотность |
|
|||||||||||||||||
Б |
|
|
|
S0 |
( ) 2 A ( ). |
|
|
|
|
|
|
|
|
|
(2.58) |
|||
Как известно, |
периодический |
сигнал можно представить |
рядом |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фурье в тригонометрической форме |
f ( t ) |
A0 An cos( n 1 |
n ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
(см. (2.24)), что позволяет, основываясь на соотношениях (2.57) и (2.58),
