
- •«Алгебра және геометрия» пәні
- •1. Матрицалар операциялары. Кері матрица және оны есептеу әдістері. Матрицалар және оларға амалдар қолдану
- •2 Анықтауыштың әр түрлі түсініктері. N-ші ретті анықтауыштар және оның қасиеттері. Матрица туындыларының анықтауышы.
- •Үшінші ретті анықтауыш туралы түсінік
- •Анықтауыштың қасиеттері
- •3 Сызықты алгебра теңдеуін шешу саны және құрылымы.
- •4 Кеңістіктегі түзу теңдеу. Екі түзудің өзара орналасуы. Екі түзудің арақашықтығы
- •Кеңістікте нүкте мен бағыттаушы векторы арқылы берілген түзудің теңдеуі
- •Кеңістіктегі түзудің жалпы теңдеуі
- •5.Екінші ретті қисықтардың канондық теңдеулері. Эллипс пен гиперболаның эксцентриситеттері мен директрисалары.
«Алгебра және геометрия» пәні
-
Матрицалар операциялары. Кері матрица және оны есептеу әдістері.
-
Анықтауыштың әр түрлі түсініктері. n-ші ретті анықтауыштар және оның қасиеттері. Матрица туындыларының анықтауышы.
-
Сызықты алгебра теңдеуін шешу саны және құрылымы.
-
Кеңістіктегі түзу теңдеу. Екі түзудің өзара орналасуы. Екі түзудің арақашықтығы.
-
Эллипс, гипербола, параболаның канондық теңдеулері. Полярлы координата жүйелеріндегі эллипс, парабола, гипербола теңдеулері.
1. Матрицалар операциялары. Кері матрица және оны есептеу әдістері. Матрицалар және оларға амалдар қолдану
 санын
А матрицасына көбейту үшін оның әрбір
элементін сол санға көбейту қажет
санын
А матрицасына көбейту үшін оның әрбір
элементін сол санға көбейту қажет
Бірдей өлшемді А және В матрицаларының қосындысы деп өлшемі А мен В өлшеміндей, элементтері А мен В элементтерінің қосындысыны тең матрицаны атайды.
А және В матрицаларының көбейтіндісі деп сij – элементтері А матрицасының i – ші жатық жолы элементтерін В матрицасының j – ші тік жолының сәйкес элементтеріне көбейтіп қосқанға тең С матрицасын атайды.
Мысал.
Берілген А=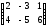 және В =
және В =
 .
Табу керек 2А+3В
.
Табу керек 2А+3В
2А+3В=
2 +3
+3 =
= +
+ =
=
= =
=

Мысал.
А=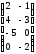 ,
В =
,
В =
 Табу керек: АВ
.
Табу керек: АВ
.
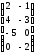
 =
= =
=
=
Кері матрица. Матрицаның керілену критерийі.
Анықтама: А(n x n) квадрат матрица, А-1 кері матрица, егер осыны А ға көбейтеміз, бірлік матрица шығады. А-1 *А=А* А-1 =Е
Ан: B(n x n) кв.мат. detB=0; онда ол ерекше матрица д.а.
Ан:
А матрицасы одақтас матрицасы деп Ат
(траспанирленген)
матрицасынының алгебралық толықтауыштарын
тұратын А* матрицасын айтамыз. 
Теорема
n-өлшемді
А матрицаның керісі табылу үшін оның
ерекше емес болуы қажет және жеткілікті.
Оның келесі формасы орындалады. А-1
= *А*
*А*
Д-у: формуланың орындалатынын көрсетсек теорема дәлелденді.

 =
=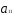
 +
+
 +....
+....

{анықтауыштың
1-қатары бойынша жіктелуі}≠detA
 +
+
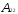 +....
+....
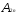 {анықтауыштың
2-қатары
бойынша жіктелуі, бірақ 2-ші
қатарда 1-қатардың
элементтері тұр.}
{анықтауыштың
2-қатары
бойынша жіктелуі, бірақ 2-ші
қатарда 1-қатардың
элементтері тұр.}
=0
Сонымен бұл көбейтіндіде диагоналіндеdetA болатын, ол қалған элементтері 0-ге тең болатын матрица шығады.
A*А*= =
А*
*A
А*
А-1
= А-1А=Е=
=
А*
*A
А*
А-1
= А-1А=Е=
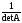 *A*А*=Е=
*A*А*=Е= =
= *
А*
*A
*
А*
*A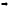 А-1=
А-1= *
А*
*
А*
(
*)
А-1=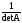

Гаус
( *) формулаасы 2, 3, 4 болатын матрицаға қолайлы. Ал өлшемділігі үлкен матрицаға Гаус Жордан алгоритмі қолданылады.
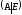 ~.....~
~.....~ =>P=А-1
=>P=А-1
Мысал.
Берілген А=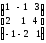 матрицасына кері матрицаны
табу керек.
матрицасына кері матрицаны
табу керек.
Шешімі.
 det
det =6
=6 .
Барлық алгебралық толықтауыштарын
есептеп табамыз
.
Барлық алгебралық толықтауыштарын
есептеп табамыз
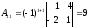 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
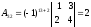 ,
,
 ,
,
 ,
,

Сөйтіп кері матрица

2 Анықтауыштың әр түрлі түсініктері. N-ші ретті анықтауыштар және оның қасиеттері. Матрица туындыларының анықтауышы.
Анықтама.
m
жатық және n тік жолдарда орналасқан
сандар кестесін m n
өлшемді тік бұрышты А матрицасы деп
атайды. Яғни
n
өлшемді тік бұрышты А матрицасы деп
атайды. Яғни
А=
Бізге
А= екінші ретті квадрат матрица берілсін.
екінші ретті квадрат матрица берілсін.
Анықтама. Екінші ретті квадрат А матрицасына сәйкесті екінші ретті анықтауыш деп санды атайды және оны былайша белгілейді
 =а11а22
– а21а12
=а11а22
– а21а12
Мысал.
Мына анықтауышты
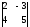 есепте.
есепте.
Шешуі.
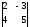 =
=
 .
.
Үшінші ретті анықтауыш туралы түсінік
Анықтама. Үшінші ретті квадрат матрицаға сәйкесті үшінші ретті анықтауыш деп
а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32 санын атап, мына символ арқылы белгілейді:
 =
а11
а22
а33
+а12
а11
а23
а31
+а13
а21
а32
-а13
а22
а31
-а12
а21
а33
-а11
а23
а32
=
а11
а22
а33
+а12
а11
а23
а31
+а13
а21
а32
-а13
а22
а31
-а12
а21
а33
-а11
а23
а32
Үшінші ретті анықтауышты есептеуде Саррюс ережесін (үшбұрыш ережесін) қолданылады:














 =
=
 +
+
 +
+
 -
-
 -
-
 -
-
 .
.
Мысал.
Мына анықтауышты
 есептеу керек.
есептеу керек.
Ол үшін үшбұрыш ережесін қолданамыз. Сонда
 =
=
