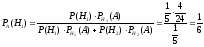«Ықтималдықтар теориясы және математикалық статистика» пәні

1. Шартты ықтималдық. Ықтималдықтарды көбейту формуласы.

2. Толық ықтималдықтар формуласы. Байес формулалары.

3. Кездейсоқ шамалар.

4. Кездейсоқ шаманың үлестірім заңы мен функциясы.

5. Дискретті және үзіліссіз кездейсоқ шамалар.

Кездейсоқ шаманың математикалық күтімі мен дисперсиясы. Қасиеттері.

1.Шартты ықтималдық. Ықтималдықтарды көбейту формуласы.

Сынақ жүргізу барысында қандай да бір А оқиғасының болуына В оқығасының болуы қалай әсер ететіні туралы сұрақ туындайды. Осы екі оқиғаның арасындағы байланысқа қарапайым мысалдар: В оқиғасының болуы А оқиғасының болуына міндетті түрде алып келеді немесе В оқиғасының болуы А оқиғасының болмауына алып келеді. Ықтималдықтар теориясында А және В оқиғаларының арасындағы байланыс шартты ықтималдық ретінде сипатталады. Ол P(A|B) А оқиғасы В оқиғасы орындалған кезде:

P(A|B) = P(AB)/P(B) (1)

Анықтама: - қандайда бір ықтималдық кеңістік . А,В – оқиғалар, .

В орындалады деп ұйғарғандағы А оқиғасының шартты ықтималдығы деп санын айтады және оны деп белгілейді .

Шартты ықтималдық қарапайым ықтималдық қасиеттерінің бәріне ие:

• 

• Егер ,

• Егер ,

• Егер А қиылыспайтын А₁ , А₂ , А₃... оқиғалардың бірігуі болса,

онда

1-мысал. Қызыл және қара түсті екі ойын сүйегі бір мезгілде лақтырылады.

а) түсетін ұпайлардың қосындысы 8 болу ықтималдығын табу керек

б) қызыл сүйекте жұп ұпай түседі деп есептеп, түсетін ұпайлардың қосындысы 8 болу ықтималдығын қайта есепте Шешуі:

А) - қызылда , - қарада түскен ұпай

6, , Ықтималдықтың классикалық анықтамасын қолданамыз

б) , , , , , - В оқиғасы орындалады деп ұйғарғандағы А оқиғасының

шартты ықтималдығы деп аталады Мұндағы А оқиғасының а) пунктіндегі есептелген ықтималдығы шартсыз ықтималдық деп аталады , ал б) пунктіндегі есептелген ықтималдығы шартты ықтималдық деп аталады .Ықтималдықтарды көбейту формуласы

(1)-ден

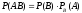
Сол сияқты

Бұл формулалар екі оқиға үшін ықтималдықты көбейту формулалары деп аталады. А,В,С- үш оқиға үшін ықтималдықты көбейту формулаласы

болады.

- оқиғалары үшін ықтималдықты көбейту формулаласы

2.Толық ықтималдықтар формуласы. Байес формулалары.

Анықтама: 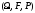- ықтималдық кеңістік . А – оқиғасы берілген .

Онда 1)

2)ø

шарттарын қанағаттандыратын үшін

(1)

теңдеуі орындалады.(1)- толық ықтималдықтар формуласы .

Жоғарыдағы шарттар орындалғанда (1) формуласымен қатар келесі формулада орындалады

(2)

(2) – Байес формуласы .

Есептер шығарғанда сынақ және А оқиғасы есептің шарттарында беріледі. гипотезаларын сынақтың берілгеніне қарай өзіміз таңдаймыз.

1-мысал.

25 емтихан билеттерінің бесеуі “жақсы ” . Екі студент бір-бір билеттен алады. Екінші студенттің “жақсы ” билет алу ықтималдығын табу керек.

Шешуі: Сынақ- екі студенттің бірінен соң бірі бір-бір билеттен алуы .

Оқиға- А={екінші студенттің “жақсы ” билет алуы }

Гипотезалар ( көмекші оқиғалар ):

={бірінші студенттің “жақсы ” билет алуы }

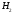={ бірінші студенттің “жақсы ” билет алмауы }

- ?

Бұларды толық ықтималдықтар формуласына қоямыз .

, , ,

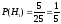2-мысал.

Жоғарыдағы сынақта екінші студенттің “жақсы ” билет алғаны белгілі болса, бірінші студенттің “жақсы ” билет алу ықтималдығы.

Шешуі: Байес формуласы бойынша шығады