
- •1. Краткая характеристика систем класса Maple
- •Урок 1.
- •Первое знакомство с системой Maple 7
- •Краткая характеристика систем класса Maple
- •2. Версии систем класса Maple. Версии систем класса Maple
- •3. Об ошибках в символьных вычислениях Об ошибках в символьных вычислениях
- •4. Ядро и пакеты Maple 7 Ядро и пакеты Maple 7
- •5. Языки системы Maple 7 Языки системы Maple 7
- •6. Ориентация систем Maple Ориентация систем Maple
- •7. Возможности предшествующей версии Maple 6 Возможности предшествующей версии Maple 6
- •8. Новые возможности системы Maple 7 Новые возможности системы Maple 7
- •9. Установка системы Maple 7 на пк Установка системы Maple 7 на пк
- •10. Установка системы Maple 7 Установка системы Maple 7
- •13. Меню системы Maple 7 Меню системы Maple 7
- •14. Палитры ввода математических символов Палитры ввода математических символов
- •15. Всплывающие подсказки Всплывающие подсказки
- •16. Основы работы с Maple 7 в диалоговом режиме Основы работы с Maple 7 в диалоговом режиме
- •17. Понятие о функциях и операторах Понятие о функциях и операторах
- •18. Обработка и индикация ошибок Обработка и индикация ошибок
- •20. Примеры задания функции пользователя и построения ее графика Примеры задания функции пользователя и построения ее графика
- •21. Пример построения трехмерного графика поверхности Пример построения трехмерного графика поверхности
- •22. Управление формой представления документа Управление формой представления документа
- •23. Представление входных выражений в математической форме Представление входных выражений в математической форме
- •24. Символьные вычисления Символьные вычисления
- •27. Пример решения системы линейных уравнений Пример решения системы линейных уравнений
- •28. Повышение эффективности работы с системой Повышение эффективности работы с системой
- •29. Работа с контекстной панелью Работа с контекстной панелью
- •30. Контекстная панель инструментов для двумерных графиков Контекстная панель инструментов для двумерных графиков
- •31. Контекстная панель инструментов для трехмерных графиков Контекстная панель инструментов для трехмерных графиков
- •32. Строка состояния Строка состояния
- •33. Горячие клавиши системы Горячие клавиши системы
- •34. Доступ к справкам и примерам Доступ к справкам и примерам
- •2. Просмотр введения Просмотр введения
- •3. Оперативная справка по контексту Оперативная справка по контексту
- •4. Обучающий курс New User's Tour Обучающий курс New User's Tour
- •6. Правила работы со справочной системой Правила работы со справочной системой
- •7. Предметный поиск Предметный поиск
- •8. Предметный поиск с полным обзором текста справки Предметный поиск с полным обзором текста справки
- •9. История работы со справкой История работы со справкой
- •2. Меню File Меню File
- •3. Создание нового документа Создание нового документа
- •4. Открытие документа Открытие документа
- •5. Сохранение документа Сохранение документа
- •6. Запись документа на диск с переименованием Запись документа на диск с переименованием
- •7. Экспорт файлов. Экспорт файлов
- •8. Закрытие документа Закрытие документа
- •11. Печать документов Печать документов
- •12. Предварительный просмотр страниц Предварительный просмотр страниц
- •13. Установка параметров принтера Установка параметров принтера
- •14. Редактирование документов Редактирование документов
- •18. Копирование объекта в буфер Копирование объекта в буфер
- •21. Вставка из буфера обмена в документ Вставка из буфера обмена в документ
- •22. Вставка из буфера обмена в формате Maple-текста Вставка из буфера обмена в формате Maple-текста
- •26. Включение и выключение режима ввода текста Включение и выключение режима ввода текста
- •27. Операции разделения и объединения объектов
- •30. Операции вставки Операции вставки
- •37. Меню Spreadsheet Меню Spreadsheet
- •38. Работа с электронными таблицами Работа с электронными таблицами
- •44. Установка стилей. Установка стилей
- •50. Вставка объектов Вставка объектов
- •52. Что нового мы узнали?
- •2. Управление показом панели инструментов (Toolbar) Управление показом панели инструментов (Toolbar)
- •3. Управление показом контекстной панели
- •6. Установка масштаба отображения документа Установка масштаба отображения документа
- •7. Установка закладок Установка закладок
- •8. Управление показом компонентов документа Управление показом компонентов документа
- •9. Управление показом непечатаемых символов. Управление показом непечатаемых символов
- •10. Управление показом областей секций Управление показом областей секций
- •11. Управление показом областей секций Управление показом областей секций
- •12. Управление показом областей ячеек (Show Group Ranges) Управление показом областей ячеек (Show Group Ranges)
- •13. Закрытие всех секций Закрытие всех секций
- •14. Раскрытие всех секций Раскрытие всех секций
- •15. Работа с параметрами Maple 7 Работа с параметрами Maple 7
- •16. Управление выводом Управление выводом
- •17. Установка режима вставки новой ячейки Установка режима вставки новой ячейки
- •18. Задание браузера Задание браузера
- •21. Установка параметров вывода Установка параметров вывода
- •22. Контроль за предполагаемыми переменными (Assumed Variables) Контроль за предполагаемыми переменными (Assumed Variables)
- •23. Управление показом графиков Управление показом графиков
- •18A.Gif
- •26. Работа с окнами Работа с окнами
- •32. Закрытие всех окон одновременно Закрытие всех окон одновременно
- •2. Зарезервированные слова Зарезервированные слова
- •3. Выражения и основы работы с ними Выражения и основы работы с ними
- •7. Простые типы данных Простые типы данных
- •12. Списки выражений Списки выражений
- •13. Массивы, векторы и матрицы Массивы, векторы и матрицы
- •14. Таблицы Таблицы
- •16. Неисполняемые программные комментарии Неисполняемые программные комментарии
- •17. Константы Константы
- •18. Строковые константы Строковые константы
- •19. Встроенные в Ядро константы Встроенные в ядро константы
- •20. Идентификация констант.
- •22. Переменные Переменные
- •23. Идентификаторы (имена) переменных Идентификаторы (имена) переменных
- •24. Присваивание переменным значений Присваивание переменным значений
- •25. Отмена операции присваивания и команда restart Отмена операции присваивания и команда restart
- •2. Бинарные (инфиксные) операторы Бинарные (инфиксные) операторы
- •4. Унарные арифметические операторы Унарные арифметические операторы
- •5. Оператор % и команда history Оператор % и команда history
- •7. Специальные типы операторов Специальные типы операторов
- •8. Функциональные операторы Функциональные операторы
- •9. Нейтральные операторы, определяемые пользователем Нейтральные операторы, определяемые пользователем
- •10. Определение операторов с помощью оператора define Определение операторов с помощью оператора define
- •11. Математические функции Математические функции
- •12. Некоторые целочисленные функции и факториал Некоторые целочисленные функции и факториал
- •13. Тригонометрические функции Тригонометрические функции
- •14. Обратные тригонометрические функции Обратные тригонометрические функции
- •15. Гиперболические функции Гиперболические функции
- •22. Преобразование списков в векторы и матрицы Преобразование списков в векторы и матрицы
- •23. Операции с векторами Операции с векторами
- •27. Интерактивный ввод строк Интерактивный ввод строк
- •28. Обработка строк Обработка строк
- •29. Преобразование строки в математическое выражение Преобразование строки в математическое выражение
- •2. Основной способ задания функции пользователя Основной способ задания функции пользователя
- •3. Графическая визуализация результатов выполнения функций пользователя Графическая визуализация результатов выполнения функций пользователя
- •4. Импликативные функции Импликативные функции
- •5. Условные выражения Условные выражения
- •7. Операторы пропуска и прерывания Операторы пропуска и прерывания
- •8. Процедуры и процедуры-функции Процедуры и процедуры-функции
- •9. Оператор возврата значения return Оператор возврата значения return
- •10. Статус переменных в процедурах и циклах Статус переменных в процедурах и циклах
- •11. Объявления переменных локальными с помощью оператора local Объявления переменных локальными с помощью оператора local
- •12. Объявления переменных глобальными с помощью слова global Объявления переменных глобальными с помощью слова global
- •13. Функция вывода сообщений об ошибках error Функция вывода сообщений об ошибках error
- •14. Ключи в процедурах Ключи в процедурах
- •Ключ remember
- •Ключ builtin
- •16. Средства контроля и отладки процедур Средства контроля и отладки процедур
- •17. Работа с отладчиком программ Работа с отладчиком программ
- •18. Операции ввода и вывода Операции ввода и вывода
- •19. Создание своей библиотеки процедур Создание своей библиотеки процедур
- •20. Запись и считывание данных Запись и считывание данных
- •21. Вывод в специальных форматах Вывод в специальных форматах
- •22. Генерация кодов на языке Фортран Генерация кодов на языке Фортран
- •23. Генерация кодов на языке с Генерация кодов на языке с
- •24. Дополнительные возможности Maple-языка Дополнительные возможности Maple-языка
- •25. Модули. Модули
- •26. Макросы Макросы
- •27. Внешние вызовы Внешние вызовы
- •28. Вызов внешних процедур, написанных на языке с Вызов внешних процедур, написанных на языке с
- •29. Что нового мы узнали? Что нового мы узнали?
- •1. Вычисление сумм последовательностей Урок 8. Математический анализ.
- •2. Последовательности с заданным числом членов Последовательности с заданным числом членов
- •3. Суммы с заданным пределом Суммы с заданным пределом
- •17. Вычисление кратных интегралов Вычисление кратных интегралов
- •18. Вычисление пределов функций Вычисление пределов функций
- •19. Разложение функций в ряды Разложение функций в ряды
- •20. Разложение в ряды Тейлора и Маклорена Разложение в ряды Тейлора и Маклорена
- •21. Пример документа — разложение синуса в ряд Пример документа — разложение синуса в ряд
- •23. Решение одиночных нелинейных уравнений Решение одиночных нелинейных уравнений
- •33. Решение рекуррентных уравнений — rsolve Решение рекуррентных уравнений — rsolve
- •34. Решение уравнений в целочисленном виде — isotve Решение уравнений в целочисленном виде — isolve
- •35. Функция msolve. Функция msolve
- •36. Что нового мы узнали?
- •2. Работа с уровнями вложенности выражений Работа с уровнями вложенности выражений
- •3. Преобразование выражений в тождественные формы Преобразование выражений в тождественные формы
- •4. Преобразование выражений Преобразование выражений
- •5. Контроль за типами объектов Контроль за типами объектов
- •6. Подстановки
- •15. Комплектование по степеням Комплектование по степеням
- •16. Программирование символьных операций Программирование символьных операций
- •2. Основная функция построения двумерных графиков — plot Основная функция построения двумерных графиков plot
- •3. Задание координатных систем двумерных графиков Задание координатных систем двумерных графиков
- •4. Управление стилем и цветом линий двумерных графиков Управление стилем и цветом линий двумерных графиков
- •5. Основные типы двумерных графиков Основные типы двумерных графиков
- •6. Управление диапазоном изменения переменной и значения функции Управление диапазоном изменения переменной и значения функции
- •9. Графики нескольких функций на одном рисунке Графики нескольких функций на одном рисунке
- •11. Графики функций, заданных своими именами Графики функций, заданных своими именами
- •12. Графики функций с ординатами, заданными вектором Графики функций с ординатами, заданными вектором
- •16. Графики функций в полярной системе координат Графики функций в полярной системе координат
- •17. Построение трехмерных графиков Построение трехмерных графиков
- •18. Параметры функции plot3d Параметры функции plot3d
- •19. Выбор и пересчет координат трехмерных графиков Выбор и пересчет координат трехмерных графиков
- •Invcasscylindrical:
- •Invellcylindrical:
- •Invoblspheroidal:
- •Invprospheroldal:
- •20. Построение поверхностей Построение поверхностей
- •21. Построение фигур в различных системах координат Построение фигур в различных системах координат
- •23. Масштабирование трехмерных фигур и изменение углов их обзора Масштабирование трехмерных фигур и изменение углов их обзора
- •25. Быстрое построение графиков Быстрое построение графиков
- •26. Быстрое построение трехмерных графиков smartplot3d Быстрое построение трехмерных графиков smartplot3d
- •27. Специальные приемы построения трехмерных графиков Специальные приемы построения трехмерных графиков
- •30. Двумерные и трехмерные графические структуры Двумерные и трехмерные графические структуры
- •31. Графические структуры двумерной графики Графические структуры двумерной графики
- •32. Графические структуры трехмерной графики Графические структуры трехмерной графики
- •1. Пакет plots Урок 12. Расширенные средства графики
- •2. Построение графиков функций в двумерной полярной системе координат
- •3. Построение двумерных графиков типа implidtplot
- •4. Построение графиков линиями равного уровня
- •5. График плотности
- •6. Двумерный график векторного поля
- •7. Трехмерный график типа implidtplot3d
- •8. Графики в разных системах координат
- •9. Графики типа трехмерного поля из векторов
- •10. Контурные трехмерные графики
- •11. Техника визуализации сложных пространственных фигур
- •13. Проигрыватель анимированной графики
- •14. Построение двумерных анимированных графиков
- •15. Построение трехмерных анимационных графиков
- •16. Анимация с помощью параметра insequence
- •17. Графика пакета plottools
- •18. Примеры применения двумерных примитивов пакета plottools
- •19. Примеры применения трехмерных примитивов пакета plottools
- •20. Построение графиков из множества фигур
- •21. Анимация двумерной графики в пакете plottools.
- •22. Анимация трехмерной графики в пакете plottools
- •23. Расширенные средства графической визуализации
- •24. Визуализация решения систем линейных уравнений
- •25. Визуализация решения систем неравенств
- •26. Конформные отображения на комплексной плоскости
- •27. Графическое представление содержимого матрицы
- •28. Визуализация ньютоновских итераций в комплексной области
- •29. Визуализация корней случайных полиномов
- •30. Визуализация поверхностей со многими экстремумами
- •31. Визуализация построения касательной и перпендикуляра
- •32. Визуализация вычисления определенных интегралов
- •33. Визуализация теоремы Пифагора
- •34. Визуализация дифференциальных параметров кривых
- •36. Построение сложных фигур в полярной системе координат
- •37. Построение сложных фигур импликативной графики
- •38. Расширенная техника анимации
- •39. Наблюдение кадров анимации поверхности
- •40. Новая функция для построения стрелок arrow
- •41. Построение сложных комбинированных графиков
- •42. Что нового мы узнали?
- •1. Основные средства решения дифференциальных уравнений Урок 13. Решение дифференциальных уравнений
- •2. Решение оду первого порядка
- •3. Решение дифференциальных уравнений второго порядка
- •4. Решение систем дифференциальных уравнений
- •5. Численное решение дифференциальных уравнений
- •6. Дифференциальные уравнения с кусочными функциями
- •8. Инструментальный пакет решения дифференциальных уравнений dEtools.
- •9. Основные функции пакета dEtools
- •11. Функция dEplotna пакета dEtools
- •12. Функция dEplot3d из пакета dEtools
- •13. Функция pdEplot пакета dEtools.
- •14. Графическая функция dfieldplot
- •15. Графическая функция phaseportrait
- •16. Углубленный анализ дифференциальных уравнений
- •17. Проверка ду на автономность
- •18. Контроль уровня вывода решения ду
- •19. Приближенное полиномиальное решение ду
- •20. Что нового мы узнали?
- •1. Назначение пакетов расширения и обращение к ним Урок 14. Математические пакеты
- •2. Обзор пакетов
- •3. Новые пакеты Maple 7
- •4. Получение информации о конкретном пакете
- •5. Пакеты функций комбинаторики
- •6. Пакет combstruct
- •7. Пакет финансово-экономических функций finance
- •8. Пакет ортогональных многочленов orthopoly
- •10. Работа с пакетом sumtools
- •11. Пакет реализации степенных разложений powseries
- •12. Примеры применения пакета powseries
- •13. Пакет числовой аппроксимации numapprox
- •14. Разложение функции в ряд Лорана
- •15. Паде-аппроксимация аналитических функций
- •16. Паде-аппроксимация с полиномами Чебышева
- •17. Наилучшая минимаксная аппроксимация
- •18. Наилучшая минимаксная аппроксимация по алгоритму Ремеза
- •19. Другие функции пакета
- •20. Пакет интегральных преобразований inttrans
- •21. Прямое и обратное преобразования Лапласа
- •22. Прямое и обратное преобразования Фурье
- •23. Вычисление косинусного и синусного интегралов Фурье
- •30. Функция построения в-сплайновых кривых BsplineCurve
- •37. Функции для работы с полиномами
- •39. Функции преобразования полиномов в рое и обратно
- •40. Что нового мы узнали?
- •1. Основные определения линейной алгебры Урок 15. Пакеты линейной алгебры и функциональных систем
- •3. Интерактивный ввод матриц
- •6. Решение систем линейных уравнений.
- •7. Пакет линейной алгебры с алгоритмами nag LinearAlgebra
- •8. Примеры матричных операций с применением пакета LinearAlgebra
- •10. Загрузка пакета расширения Matlab
- •11. Типовые матричные операции пакета расширения Matlab
- •13. Пакет анализа линейных функциональных систем LinearFunctionalSystems
- •14. Тестовые функции пакета LinearFunctionalSystems
- •15. Функции решения линейных функциональных систем
- •16. Вспомогательные функции
- •17. Примеры применения пакета LinearFunctiftnalSystems
- •1. Пакет решения задач линейной оптимизации simplex Урок 16. Обзор пакетов специального назначения
- •2. Функции maximize и minimize
- •3. Прочие функции пакета simplex.
- •5. Пример применения расчетных функций пакета geometry
- •8. Пример применения пакета geom3d
- •9. Пакет для работы с алгебраическими кривыми algcurves
- •10. Примеры применения пакета algcurves
- •12. Новая функция Maple 7 plot_real_curve
- •13. Пакет функций теории графов networks
- •14. Примеры применения пакета networks
- •17. Генерация случайных чисел с заданным распределением
- •18. Графика статистического пакета stats
- •19. Регрессионный анализ
- •20. Пакет для студентов student
- •21. Функции интегрирования пакета student.
- •22. Иллюстративная графика пакета student
- •23. Пакет работы с тензорами tensor
- •24. Пакет Domains.
- •25. Обзор пакетов узкого назначения
- •26. Пакет функций теории чисел numtheory
- •27. Пакет для работы с р-адическими числами padic
- •28. Пакет для работы с гауссовыми целыми числами Gausslnt
- •29. Пакет алгебры линейных операторов Ore_algebra
- •30. Инструментальный пакет для линейных рекуррентных уравнений lrEtools
- •31. Пакет функций дифференциальных форм difforms
- •32. Пакет для работы с рациональными производящими функциями genfunc
- •33. Пакет операций для работы с конечными группами group
- •34. Пакет для работы с симметрией Ли liesymm
- •35. Пакет команд для решения уравнений SolveTools
- •36. Пакет для работы с таблицами Spread.
- •37. Пакет генерации кодов codegen
- •38. Пакет создания контекстных меню context
- •39. Пакет организации многопроцессорной работы process
- •40. Новые пакеты системы Maple 7
- •41. Пакет для работы с рядами ортогональных многочленов OrthogonalSeries.
- •43. Пакет xmlTools
- •44. Пакет создания внешних программ ExternatCaUing
- •45. Пакет линейных операторов LinearOperators
- •46. Пакет для работы со случайными объектами RandomTools
- •47. Пакет для работы со списками ListTools
- •48. Что нового мы узнали?
- •1. Небольшое введение Урок 17. Примеры решения научно-технических задач
- •2. Выбор аппроксимации для сложной функции
- •3. Аппроксимации рядом Тейлора
- •4. Паде-аппроксимация
- •6. Аппроксимация Чебышева-Паде
- •7. Минимаксная аппроксимация
- •8. Эффективная оценка рациональных функций
- •9. Сравнение времен вычислений
- •10. Преобразование в код Фортрана или с
- •11. Моделирование физических явлений
- •13. Разделение изотопов
- •15. Моделирование и расчет электронных схем
- •16. Малосигнальный анализ усилителя на полевом транзисторе
- •21. Что нового мы узнали?
- •1. Анализ функций Урок 9. Анализ функций и полиномов.
- •4. Определение точек нарушения непрерывности Определение точек нарушения непрерывности
- •5. Нахождение сингулярных точек функции
- •7. Пример анализа сложной функции Пример анализа сложной функции
- •8. Функции из отдельных кусков Функции из отдельных кусков
- •9. Простые примеры применения функции piecewise Простые примеры применения функции piecewise
- •10. Работа с функциями piecewise Работа с функциями piecewise
- •12. Выделение коэффициентов полиномов Выделение коэффициентов полиномов
- •13. Оценка коэффициентов полинома по степеням Оценка коэффициентов полинома по степеням
- •14. Оценка степеней полинома Оценка степеней полинома
- •17. Вычисление корней полинома Вычисление корней полинома
- •18. Основные операции с полиномами Основные операции с полиномами
- •20. Интерполяция и аппроксимация функциональных зависимостей. Интерполяция и аппроксимация функциональных зависимостей
- •21. Аппроксимация аналитически заданных функций Аппроксимация аналитически заданных функций
- •22. Полиномиальная интерполяция табличных данных Полиномиальная интерполяция табличных данных
- •23. Сплайн-интерполяция и аппроксимация Сплайн-интерполяция и аппроксимация
- •24. Прямое и обратное z-преобразования Прямое и обратное z-преобразования
- •25. Что нового мы узнали? Что нового мы узнали?
9. Сравнение времен вычислений
Сравнение времен вычислений
Теперь определим время, необходимое для вычисления функции/(л:) в 1000 точек, используя первоначальное интегральное определение, и сравним его с временем, требующимся для схемы MinimaxApprox в виде непрерывной дроби. Так как наше приближение будет давать только 6 точных цифр, мы также потребуем 6 точных цифр и от интегрального представления функции:
> Digits :=б: St :=time():
> seq( evalf(f(i/250.0)), i = 1..1000 ):
> oldtime := time() - st;
oldtime-81.805
В процессе вычислений с использованием представления рациональной функции в виде непрерывной дроби иногда требуется внести несколько дополнительных цифр точности для страховки. В данном случае достаточно внести две дополнительные цифры. Итак, новое время вычислений:
> Digits := 8: st := tirae():
> seq( MinimaxApprox(i/250.0), i = 1..1000 ):
> newtime :» time()- st;
newtime:= .694
Ускорение вычисления при аппроксимации есть:
> SpeedUp := oldtime/newtime;
SpeedUp:=U7.S7464
Мы видим, что процедура вычислений, основанная на MinimaxApprox, выполняется почти в 120 раз быстрее процедуры с использованием исходного интегрального определения. Это просто феноменальный успех, полностью оправдывающий время, потерянное на предварительные эксперименты по аппроксимации и ее оптимизации! Разумеется, при условии, что вы будете применять эту аппроксимацию многократно.
10. Преобразование в код Фортрана или с
Преобразование в код Фортрана или С
Один из поводов разработки эффективной аппроксимации для вычисления математической функции заключается в создании библиотек подпрограмм для популярных языков программирования высокого уровня, таких как Фортран или С. В Maple имеются функции преобразования на любой из этих языков. Например, мы можем преобразовывать формулу для минимаксной аппроксимации в код Фортрана.

Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на два порядка (!) при весьма приличной точности в б верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple 7 позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач.
16.gif

11. Моделирование физических явлений
Моделирование физических явлений
Расчет траектории камня с учетом сопротивления воздуха
Вы хотите метнуть камень в огород вашего вредного соседа? Разумеется, во время его отсутствия. Давайте промоделируем эту ситуацию, предположив два актуальных случая: дело происходит на Луне и на Земле. В первом случае сопротивления воздуха (как и его самого) нет, а в другом — сопротивление воздуха есть и его надо учитывать. Иначе камень упадет в ваш огород, а не в огород соседа!
Итак, пусть подвернувшиеся под руку камни с массой 500 и 100 г брошены под углом 45° к горизонту со скоростью Vo = 20 м/с. Найдем их баллистические траектории, если сила сопротивления воздуха Fтр=А*V, где А=0,1 Н*с/м. Сравним их с траекториями, получающимися без учета сопротивления воздуха.
Начнем с подключения пакета plots, нужного для визуализации данной задачи:
> restart;
> with(plots):
Warning, the name changecoords has been redefined
Составим параметрические уравнения для проекций скорости на оси координат:
> Vox:=Vo*cos(a1pha):Voy:=Vo*sin(alpha):
Vox:= Focos(a)
Voy :=Vo sin(a)
Мы рассматриваем два случая: камень массой 500 г и камень массой 100 г. Поскольку для каждого случая мы предусматриваем расчет в двух вариантах (с учетом сопротивления воздуха и без такого учета), то мы должны составить 4 системы дифференциальных уравнений (ДУ). Каждая система состоит из двух ДУ второго порядка и вид этих систем известен из курса физики. Ниже представлено задание этих систем ДУ (для первой системы дан вывод ее вида):

Зададим исходные числовые безразмерные данные для расчета:

Выполним решение заданных систем ДУ:

Создадим графические объекты — результаты решения систем ДУ:
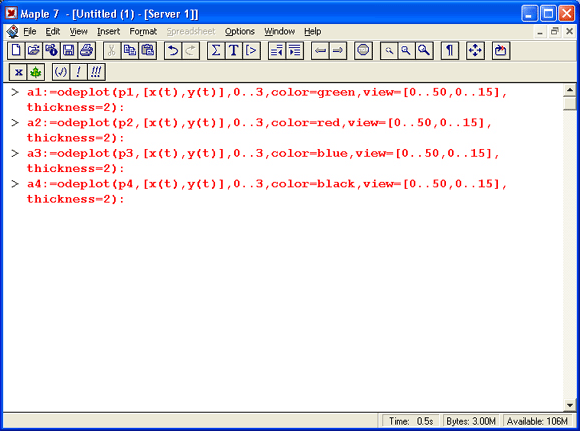
Построим графики траекторий для первого случая:
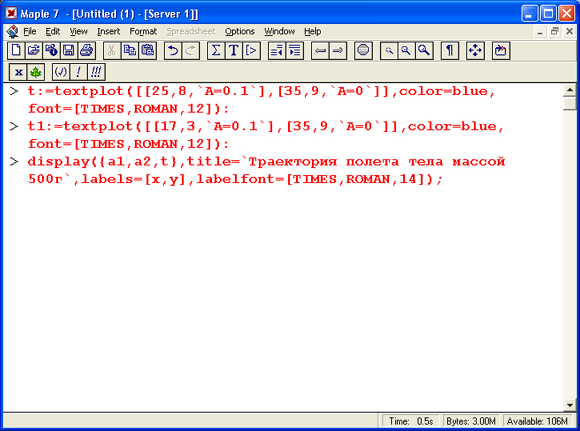
Графики траекторий полета камня с массой 500 г представлены на рис. 17.6.

Рис. 17.6.Баллистические траектории камня с массой 500 г
Теперь построим графики траекторий для второго случая:
> display({a3,a4,t1},title='Tpaeкт. полета тела массой 100 г, labels=[x.у], labelfont=[TIMES.ROMAN,14]):
Они представлены на рис. 17.7.

Рис. 17.7.Баллистические траектории камня при массе 100 г
Из проведенных расчетов и графиков видно, что при учете силы сопротивления воздуха дальность и высота полета сильно уменьшаются по сравнению с полетом в вакууме, и эта разница зависит от массы тела, поэтому при небольшой массе тела сопротивлением воздуха пренебрегать нельзя.
17.gif

18.gif

19.gif

20.gif

21.gif

22.gif

23.gif

12. Движение частицы в магнитном поле
Движение частицы в магнитном поле
От реального мира перейдем к микромиру. Пусть микрочастица массой 9* 10-31кг и зарядом +1,6*10"19Кл влетает в магнитное поле с индукцией В = 0,1 Тл под углом а=80°. Рассчитаем траекторию движения частицы при начальной скорости Vo= 1*107м/с:
> restart;
Сила Лоренца, действующая на движущуюся частицу F = q*(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z:
[v.B]x=vy*Bz-vz*By [v,B]y=vz*Bx-vx*Bz [v,B]z=vx*By-vy*Bz
В соответствии с этим известные из курса физики дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:

Зададим исходные числовые данные (опустив размерности):
> q:=-1.6e-19: massa:=9.1e-31: V:=le7: alpha:=80*Pi/180:
> Vx:=V*cos(alpha): Vy:=V*sin(alpha): Ex:=0:Ey:=0:Ez:=0: Bx:=0.1:By:=0: Bz:=0:
Построим траекторию движения частиц в пространстве:
> with(DEtools):DEplot3d({sys},{x(t),y(t),z(t)},t=0..2e-9, [[x(0)=O,D(x)(0)=Vx,y(0)==0,D(y)(0)=Vy,z(0)=0,D(z)(0)=0]], stepsize=le-ll,orientation=[24.117]):
Полученная траектория представлена на рис. 17.8. Она имеет вид спирали в пространстве. При этом скорость движения частицы вдоль оси х неизменна, а вдоль осей у и z имеет характерную колебательную компоненту. Случай явно куда менее тривиальный, чем полет камня, описанный выше.

Рис. 17.8.Траектория движения частицы в магнитном поле
Мы можем найти аналитическое представление для траектории частицы в виде параметрически заданной (с параметром времени t) системы из трех уравнений:

Моделирование движения заряженной частицы в пространстве с магнитным полем показывает, что для принятых для моделирования параметров решаемой задачи, движение частицы происходит по спиралеобразной траектории. Получен как график траектории движения частицы, так и аналитические уравнения, описывающие это движение.
24.gif

25.gif

26.gif

