9. Орталық шектік теорема.

(Ω, ℱ, Р)-дан өзара тәуелсіз және бәрдей үлестірілген кездейсоқ шамалар тізбегі беріліп М=a, D , онда

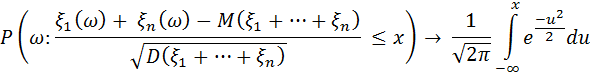
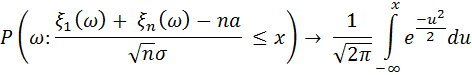
(n)

M(

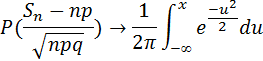
кездейсоқ шамалары үшін бірқатар белгілеулер енгізелік: математикалық үміттер-математикалық үміттердің қосындысы- дисперсиялар дисперсиялардың қосындысы-. Нормаланған қосынды болатын кездейсоқ шамасын құрамыз: кездескендей арқылы қалыпты үлестірім заңын білгілейміз: , А-а Егер шектік қатынасы орындалса, онда кездейсоқ шамалар орталық шектік заңға бағынады деп атайды.

10. Эмпирикалық үлестірім функциясы. Таңдамалық орта және таңдамалық дисперсия

- бақыланатын кездейсоқ шама

- - ден алынған таңдама болсын (34.1)

Эмперикалық үлестірім функциясы деп – нүктесінде

(34.2)

теңдігімен анықталатын функциясын айтады. Мұндағысаныбекітілгендегі (34.1) тізбегіндегі-тен аспайтын-лар саны.Теорема:(А.Н. Колмогоров) - бақыланатын кездейсоқ шама, - оның теориялық үлестірім функциясы болсын, ондаүшін

Математикалық күтімнің бағасы – таңдамалық орта

- бақыланатын кездейсоқ шамасы берілген. Оның үлестірімі параметрімен бірмәнді анықталғаны белгілі болсын (мысалы, бинамиамды үлестірім: белгісіз параметрлер ретінде; көрсеткішті үлестірім :; қалыпты үлестірім :; т.с.с.).

Мақсат: параметрлері үшін баға құру.

Ол үшін таңдама керек:

- -ден алынған таңдама.

Баға ретінде: (36.1)

таңдамалық орта деп аталатын кездейсоқ шама алынады. Бағаны бұлай алуға себеп болатын математикалық күтімнің практикалық мағынасы және үлкен сандар заңы.

Белгісіз дисперсия үшін баға – таңдамалық дисперсия

- бақыланатын кездейсоқ шама болсын, оның дисперсиясы белгісіз болсын.

- таңдама

Мақсат: - қа баға құру

Ол үшін дисперсияның анықтамасын еске түсірейік:

Бұдан баға

(37.1)

болуы мүмкін деген ойға келеміз.

- ығыспаған баға . Бұдан бұл баға үшін ығыспаған болмайтындығы көрініп тұр. Ығыспаған баға алу үшін бұл теңдіктің екі жағында- ге көбейтеміз. Сонда

Бұдан бұны деп белгілейік:

(37.2)

(37.1) – дисперсияның ығысқан бағасы деп аталады

(37.2) – дисперсияның ығыспаған бағасы деп аталады.

11. Бағалар. Бағалардың сұрыптамасы (ығыстырылмағандық, тиянақтылық, эффективтілік).

- үлестірім функциялар жиынтығы, мұндағы

- белгісіз параметр деп аталады, ал - белгісіз параметрлер жиыны

Есептің қойылуы: Қандайда бір үшін сәйкесүлестірім функциясы - дің үлестірім функциясы болып табылады, яғни .

Мәселе – сол -ді таңдамадан пайдаланып жуықтап табу керек .

Қойылған есепті шешу үшін -ден алынған таңдаманы пайдаланамыз.- белгісіз параметрінің мағынасына қарай ( ол әртүрлі мысалдарда әрқалай болады)

функциясын құрады және ол арқылы мына функцияға келеді

.

Бұл функция - белгісіз параметрініңбағасы деп аталады.

- ге келесі талаптар қойылады:

1. Егер үшінболса, онда- бағасыығыспаған баға деп аталады.

2. Егер үшінболса, онда- бағалар тізбегітиянақты деп аталады.

3. Егер - бағасы

теңдігін қанағаттандырса, онда - бағасыэффективті деп аталады.