4. Кері матрица. Матрицаның керілену критерийі.

Анықтама: А(n x n) квадрат матрица, А^-1 кері матрица, егер осыны А ға көбейтеміз, бірлік матрица шығады. А^-1 *А=А* А^-1 =Е

Ан: B(n x n) кв.мат. detB=0; онда ол ерекше матрица д.а.

Ан: А матрицасы одақтас матрицасы деп А^т (траспанирленген) матрицасынының алгебралық толықтауыштарын тұратын А* матрицасын айтамыз.

Теорема n-өлшемді А матрицаның керісі табылу үшін оның ерекше емес болуы қажет және жеткілікті. Оның келесі формасы орындалады. А^{-1 =}*А^*

Д-у: формуланың орындалатынын көрсетсек теорема дәлелденді.

=++....

{анықтауыштың 1-қатары бойынша жіктелуі}≠detA ++....{анықтауыштың 2-қатары бойынша жіктелуі, бірақ 2-ші қатарда 1-қатардың элементтері тұр.}

=0

Сонымен бұл көбейтіндіде диагоналінде detA болатын, ол қалған элементтері 0-ге тең болатын матрица шығады.

A*А^*== А^* *A А* А^-1 = А^-1 А=Е=

*A*А^*=Е== * А^* *A А^-1=* А^*

( *) А^-1=

Гаус

( *) формулаасы 2, 3, 4 болатын матрицаға қолайлы. Ал өлшемділігі үлкен матрицаға Гаус Жордан алгоритмі қолданылады.

~.....~=>P=А^-1

Мысал:

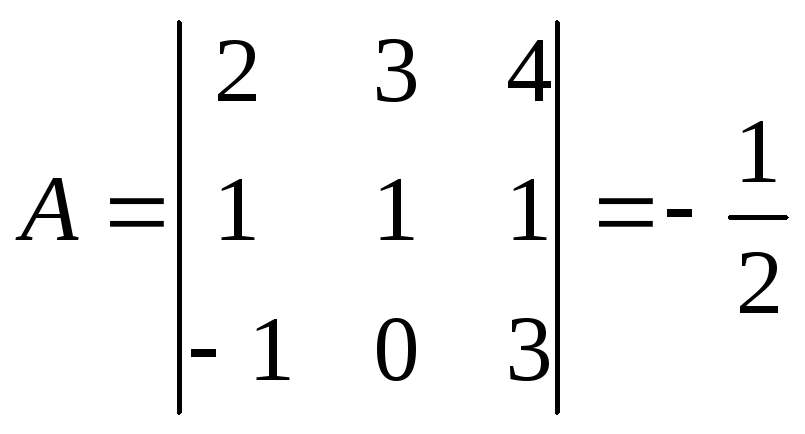
=6-3+0+4-9-0=-2

= (-1)¹⁺¹

= (-1)¹⁺²

= (-1)¹⁺³

= (-1)²⁺¹

= (-1)²⁺²

= (-1)²⁺³

= (-1)³⁺¹

= (-1)³⁺²

= (-1)³⁺³

А^-1= =*=

5. Векторлардың векторлық және аралас көбейтінділері және олардың геометриялық мағынасы.

Екі вектордың векторлық көбейтіндісі

Ан: комплонар емес болсын:

реттелген үш-гі оң үш-к д.а.егер-ң төбесінен қарағанда : ең кіші бұру сағат тіліне қарама қарсы журсе

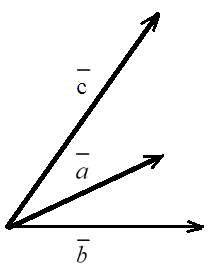
реттелген үштігі сол үштік деп аталады. Егер –ң төбесінен қарағанда ең кіші бұру сағат тілімен жүрсе

Ескерту: 1) оң болса мен оң болады. –оң болды.

Ан: Екі вектордың вектордың көбейтіндісі деп векторы =, келесі шарттарды қанағаттандыратын.

1. ==

2. ,

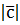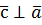3. -оң үштік c

Теорема (колениярлық шарттың 3 ші белгісі)

мен коленияр, тек болғанда ғана. Д/у:=> ║

{=>=sin^=0

Векторлық көбейтіндінің қасиеттері

1. мен ң көбейтіндісі ауыстырымды емес.

2. 

3. 

4. 

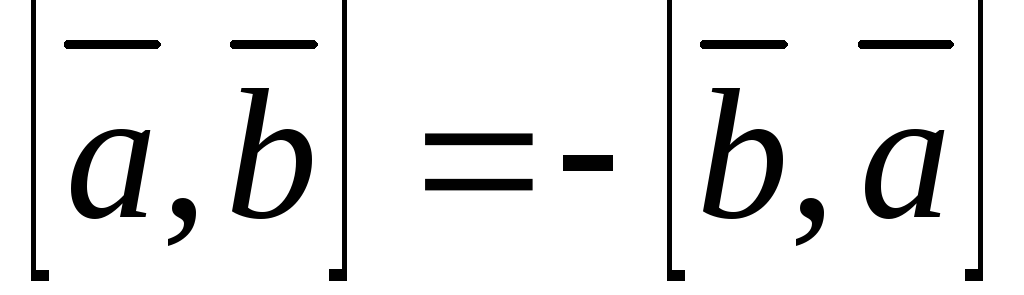
5. геометр. магынасы

=Sпар.

Sпар.==^

H=^

Теорема. Декарт координаттар жүйесінде 2 вектордың = = векторлық көбейтіндісі келесі формуласы бойынша жүреді:

=

Дәлелдеу: => jk, -оң үштік

1. ==1

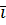2. ⊥, ⊥=>⊥; =i , =j

3 Вектордың аралас көбейтіндісі

Ан: мен ның векторлық көбейтіндісін векторына скаляр көбейтсек ның аралас көбейтіндісі шығады.

Қасиеттері:

1. 

2. 

3. 

4. 

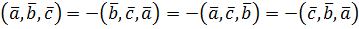
5. геометриялық мағынасы

│(ˉa,ˉb,ˉc)│= V паралеллипед.

Д/у: Егер ˉa мен ˉb коллинеар болса, онда ˉa‌‌ ‌‌ ׀׀ˉb болғандықтан [ˉa,ˉb]=Q, демек ([a b ], c)=(Q,c)=0.

Бұл жағдайда а мен b векторы коллинеар емес деп санайық, a,b,c векторын Q нүктесіне көшірейік те, а мен b векторы жататын жазықтықты P арқылы белгілейік. Онда [a,b] ┴ P және [a,b] векторының ұзындығы а мен b векторына құрылған параллелограмның ауданына тең де, a,b,[a,b] үштігі оң болады. Скаляр көбейтіндінің анықтамасы бойынша ([a,b],c)= │[a,b]│∙ {pr _[a,b] c}. Енді байқасақ ‌│ pr _[a,b] c │- a,b,c векторына құралған параллелипедтің Р жазықтығына түсірілген h биіктігіне тең.

{pr _[a,b] c}={^{h a,b,c>0}_{-h a,b,c<0}

Аралас көбейтіндіні есептеу формуласы:

Осыдан талап етілген ([a,b]c)€ V±(a,b,c) теңдігін оңай аламыз.

ˉa,ˉb,ˉc

ˉa={x₁,y_1,z₁}; ˉb={ x₂,y_2,z₂}; ˉc ={ x₃,y_3,z₃}

│ x₁,y_1,z₁│ │ x₃,y_3,z₃│

│(ˉa∙ˉb∙ˉc)│= │ x₂,y_2,z₂│=∆₁ x₃ +∆₂y₃ +∆₃z₃₌ │ x₁,y_1,z₁│

│ x₃,y_3,z₃│ │ x₂,y_2,z₂│

Теорема (компланарлық шарт): ˉa‌‌ ‌‌ ׀׀ˉb ׀׀ˉc К=>(ˉa,ˉb,ˉc)=0;