УМП Циркульные и лекальные кривые линии

Рис. 7 Внутреннее сопряжение дуг

1.4.3 Смешанное сопряжение дуг

При внутреннем сопряжении центры О1 и О2 сопрягаемых дуг радиусов

R1 и R2 лежат R1 – снаружи, а R2 - внутри сопрягающей дуги радиуса R.

Внутреннее сопряжение дуг выполняется в следующей последователь-

ности (рис.7 ):

1)Находим центр сопряжения, точку О пересечения дуг окружностей

срадиусами R+R1 и R-R2 соответственно концентричных окружностям с

радиусами R1 и R2;

2) Соединяем прямыми центр сопряжения О с центрами окружностей О1 и О2, которые пересекаясь с заданными окружностями определяют по-

ложение точек сопряжения А и В; 3) Строят сопряжение.

11

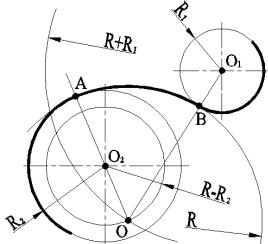
Рис.8 Смешанное сопряжение дуг

1.5.Проведение касательных

1.5.1Проведение касательной к окружности

Задана окружность с центром О и точка А (рис. 9). Требуется провести из точки А касательную к окружности.

1) Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным ОА. Чтобы найти центр О1 делят отрезок ОА пополам.

2) Точки m и n пересечения вспомогательной окружности с заданной -

искомые точки касания. Точку А соединяют прямой с точками m или n. Пря-

мая Am будет перпендикулярна к прямой Оm, так как угол АmО опирается на диаметр.

12

Рис.9 Проведение касательной к окружности

1.5.2 Проведение прямой, касательной к двум окружностям

Заданы две окружности радиусом R и R1. Требуется построить касатель-

ную к ним.

Различают два случая касания: внешнее (рис. 10) и внутреннее (рис. 11).

При внешнем касании построение выполняют следующим образом:

1) Из центра О проводят вспомогательную окружность радиусом, рав-

ным разности радиусов заданных окружностей, т. е. R - R1 . К этой окружности из центра О1 проводят касательную Оm. Построение касательной показано на рис.10.

2) Радиус, проведенный из точки О в точку n, продолжают до пересече-

ния в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm

проводят радиус 01р меньшей окружности. Прямая, соединяющая точки со-

пряжений m и р,- касательная к заданным окружностям.

Рис.10 Внешнее касание

13

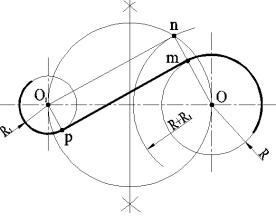
При внутреннем касании построение проводят аналогично, но вспомо-

гательную окружность проводят радиусом, равным сумме радиусов R +

R1 (рис. 11). Затем из центра O1 проводят касательную к вспомогательной ок-

ружности. Точку n соединяют радиусом с центром О. Параллельно радиусу On

проводят радиус O1р меньшей окружности. Искомая касательная проходит че-

рез точки сопряжений m и р.

Рис.11 Внутреннее касание

2. Лекальные кривые

Лекальные кривые - кривые, которые невозможно провести циркулем.

Они вычерчиваются по точкам с помощью лекал. Отсюда название -

лекальные кривые.

Общие правила вычерчивания лекальных кривых:

1)Строим точки, принадлежащие заданной кривой.

2)Тонкой плавной линией от руки соединяем полученные точки.

3)Обводим кривую по лекалу так, чтобы она охватывала своим конту-

ром 3-4 точки одновременно, но при этом некоторый участок кривой рекомен-

дуется оставить необведенным. Следующий участок лекала должен перекры-

вать ранее обведенный. Кривая должна получиться плавной, без изломов.

14

2.1.Эллипс

Эллипс - замкнутая плоская кривая, все точки которой обладают сле-

дующим свойством: сумма расстояний от любой точки эллипса до двух задан-

ных точек F1 и F2, называемых фокусами, есть величина постоянная, равная длине большой оси эллипса, т.е. |MF1|+ |MF2| = АВ (рис.12 ).

Рис.12 Эллипс

Алгоритм построения (рис.13 ).

1) Из центра О проводят две вспомогательные окружности диаметрами,

соответственно равными значениям большой оси эллипса АВ и малой СD.

2)Окружность большого диаметра делят на 12 равных частей (1,2,..,12) и

через эти точки из центра О проводят пучок лучей 0-1; 0-2; 0-3...

3)Лучи пересекают малую окружность в точках 11,21,З1,...,121.

4)Из точек деления большой окружности проводят прямые, параллель-

ные малой оси эллипса, а из точек деления малой окружности - прямые, парал-

лельные большой оси эллипса. Полученные в пересечении точки I, II, III... яв-

ляются точками, принадлежащими эллипсу, которые соединяют от руки плав-

ной кривой и обводят по лекалу.

Основой этого способа построения является то, что при преобразовании окружности в эллипс все точки окружности получают одинаковую степень сжатия, соответствующую коэффициенту сжатия эллипса, т.е. СD/АВ.

15

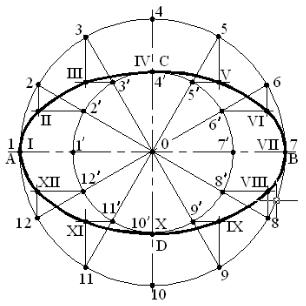
Рис.13 Построение эллипса

2.2. Спираль Архимеда

Спираль Архимеда - это плоская кривая, образуемая в результате рав-

номерного поступательного движения некоторой точки О по выходящему из нее и равномерно вращающемуся лучу. (Или, это плоская кривая, которую описывает точка, равномерно движущаяся от центра О по равномерно вра-

щающемуся радиусу.)

Точка О - полюс, отрезок t - шаг спирали.

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел закономерность построения спирали, поэтому данная кривая называется его именем. Увеличение ее шага всегда равномерно.

В настоящее время спираль Архимеда широко применяется в технике и очень распространена в природе.

Алгоритм построения (рис.14 ):

1. Заданный шаг t делят на 8 равных частей.

16

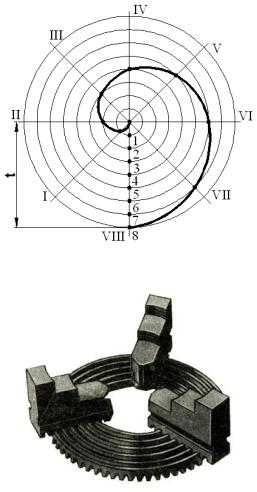
2.Из полюса спирали проводят окружность, разделяют равным шагом и делят на те же 8 частей.

3.Затем из точки О, как из центра проводят дуги радиусами 1, 2, 3.. и т.д.

до пересечения с лучом 1, 2, 3, 4.. и т.д.

4. Полученные точки и есть искомые.

Рис. 14 Спираль Архимеда

Рис. 15 Спираль Архимеда на тыльной стороне зубчатого колеса токарного патрона

2.3. Эвольвента

Эвольвента - это плоская кривая, образуемая движением любой точки окружности при ее развертывании в одну сторону с одновременным выпрям-

лением. Отрезок πD - шаг эвольвенты

17

Профиль рабочих поверхностей зубьев большинства зубчатых колес имеет эвольвентное очертание (рис.15).

Рис.15 Эвольвентный профиль зуба

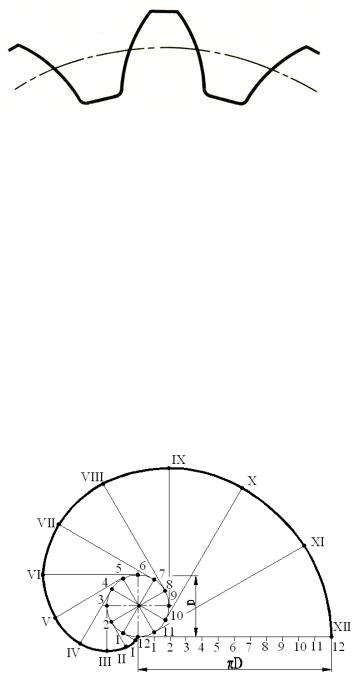
Алгоритм построения (рис.16):

1)Окружность диаметром D разделить на 12 частей.

2)Из точек деления (1,2,3...12) проводят касательные, направленные в одну и ту же сторону.

3)На касательных отложить отрезки, равные N* πD/12, где N равно но-

меру точки.

4) Полученные точки I,II,III....XII соединить.

Рис.16 Построение эвольвенты

2.4. Циклоида

Циклоида - кривая, которую можно представить как траекторию точки А, лежащей на окружности диаметра D, которая катится без скольжения:

18

а) по прямой линии;

б) по направляющей окружности радиуса R - эпициклоида;

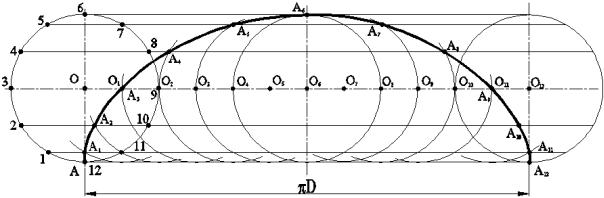
Алгоритм построения (рис.17 ):

1)Проводим окружность диаметром D.

2)Делим окружность на 12 равных частей.

3)Проводим горизонтальную прямую через центр О и откладываем 12

частей, отрезками равными хорде окружности. Проводим тонкими линиями горизонтальные прямые из точек деления окружности.

4) Из точек деления прямой (О1, О2,...) как из центра окружности прово-

дим засечки дугами радиуса D/2 до пересечения с одноименными горизон-

тальными прямыми и получаем точки циклоиды 1, 2,.. ,которые , соединяем между собой по лекалу.

Рис.17 Построение циклоиды

2.5 Парабола

Парабола – плоская кривая, каждая точка которой расположена на оди-

наковых расстояниях от заданной прямой L – директрисы.

Алгоритм построения (рис.18 ):

1) Строим по заданным параметрам (L и L1), прямоугольник ОАВС.

19

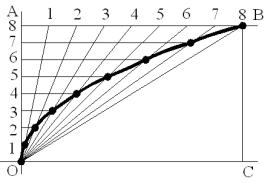
2)Отрезки АО и АВ делим на равное количество частей.

3)Соединяем вершину О с точками 1, 2, 3, ….

4)Соединяем точки 1, 2, 3, … прямыми параллельно оси ОС

5)В пересечении одноименных прямых отмечаем точки параболы.

Рис.18 Построение параболы

2.6.Синусоида

Синусоида – кривая изображающая изменение тригонометрической функции (синуса) в зависимости от изменения угла.

Алгоритм построения (рис.19):

1)Окружность диаметром D2 делят на 12 равных частей.

2)Отрезок АВ, длина которого равна длине окружности (ПD2), делят на такое же число частей.

3)Определяют точки пересечения перпендикуляров, восстановленных из точек 11, 21, …, 121 к отрезку АВ, с прямыми проведенными через точки 1, 2, …, 12 окружности, параллельно отрезку АВ.

4)Полученные точки I, II, …, XII соединяют с помощью лекала.

20