Вказівки до розв’язування задач

типового варіанту

До задачі 1

Варіант 0:

Розв’язання. а) Позначимо рівняння системи:

Вписуємо елементи системи в обчислювальну таблицю (див. 1.1, табл.1, або приклад 1, табл.2)

N п/п	X1	X2	X3	Вільни члені	Суми	Контроль
1	1	3	-1	-5	-2
2	3	2	-5	-3	-3
3	-2	-1	3	1	1
4		-7	-2	12	3	3
5		5	1	-9	-3	-3
6			3	3	6	6

Зворотний хід. Виписуємо трикутну систему згідно з рядками1, 4, 6, куди входять провідні елементи

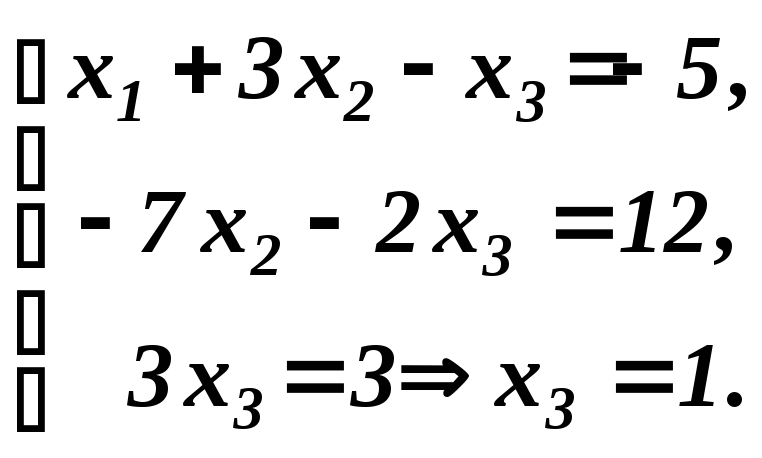
З другого рівняння трикутної системи

З першего рівняння

Відповідь:

б) Обчислимо визначники: За формулами Крамера:

в) Позначення А — матриця системи, В — стовпець вільних членів, Х — стовпець невідомих:

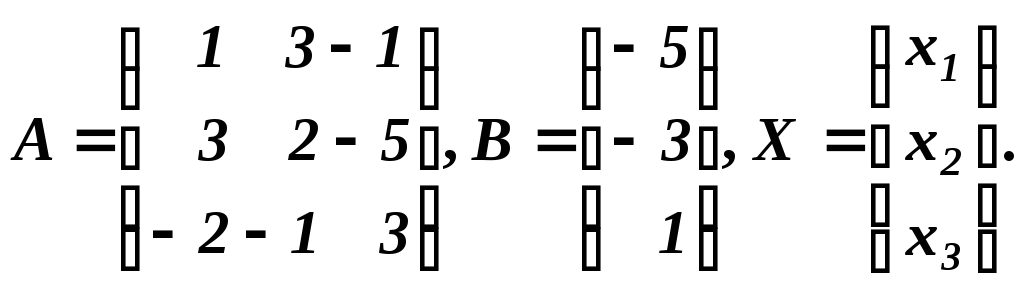
Матричний вигляд системи: АХ=В. Розв’язання цього рівняння (за умови існування оберненої матриці А^-1):

Формула оберненої матриці:

якщ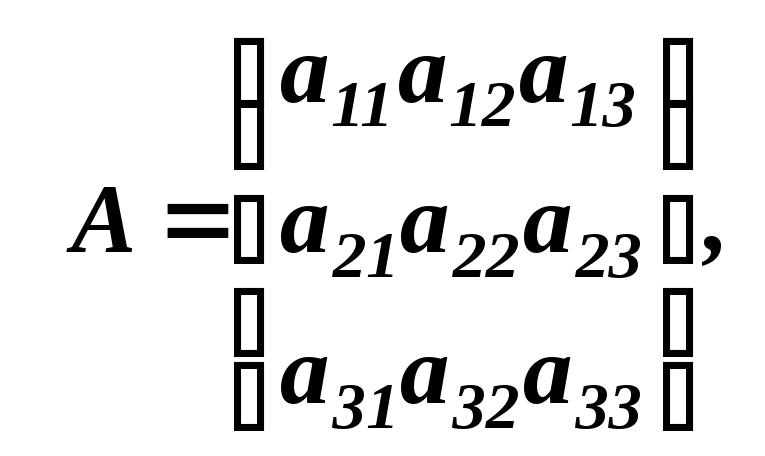о то

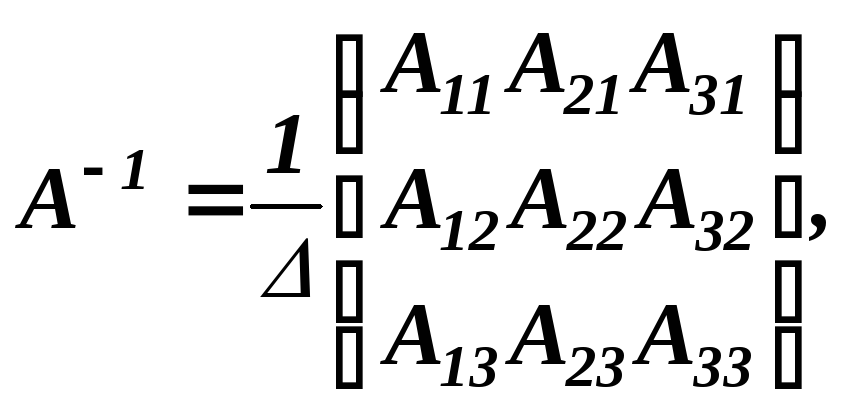
де визначник матриці А; А_ij — алгебраїчне доповнення до елементу а_ij матриці А.

У цій задачі А^-1 існує. Обчислюємо А_ij:

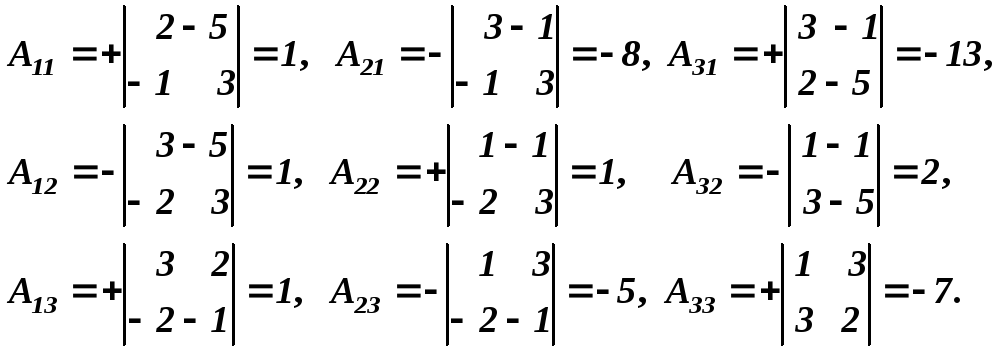
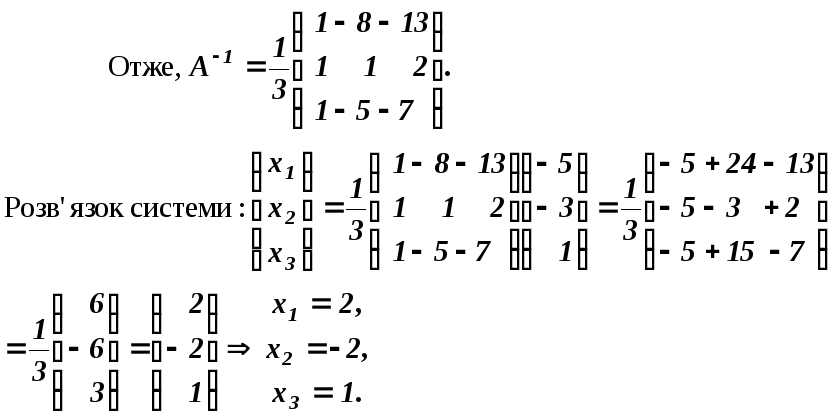
До задачі 2

Варіант 0:

Відповіді і вказівки.

(12)Використати скалярний добуток векторів (умову ортогональності). Відповідь: t =

(13)Три вектори утворюють базис тільки тоді, коли визначник, складений з кординат цих векторів, відмінний від 0:

Нехай - координати у новому базисі: .

Виконуючи дії з координатами, перепишемо цю рівність у координатному вигляді:

Розв’язок системи:

Відповідь

До задачі 3

Варіант 0:

Відповіді та вказівки.

(8) Розглянути вектори

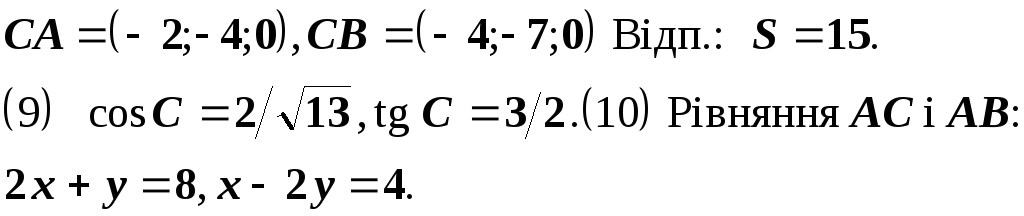
За властивістю бісектриси відстані довільної її точки N(x,y) до сторін АВ і АС рівні:Відомо, якщо то або . Тому слід розглянути два випадки: Одна з цих прямих — бісектриса внутрішнього кута, а друга —зовнішнього. Відп.: х + 3у = 4.Див. рис. 1.

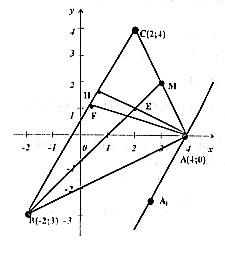
Рис. 1

До задачі 4

Варіант 0:

Розв’язання та відповіді. (1) Див. Рис. 2.

Масштаб на Ох удвічі менше, ніж на Оy і Oz.

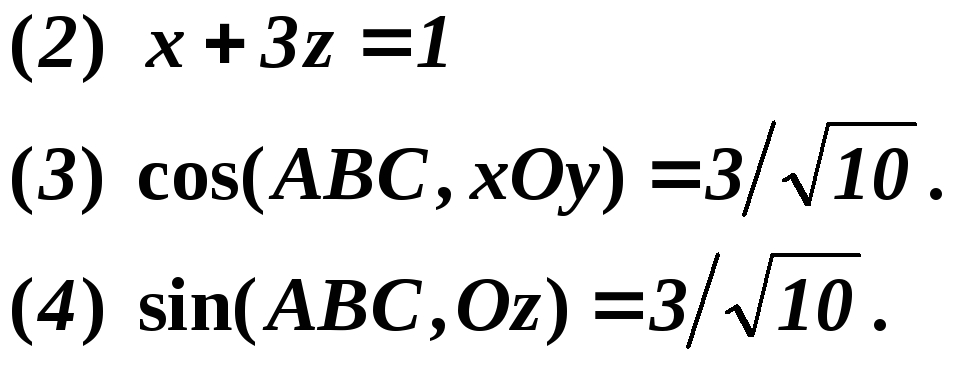
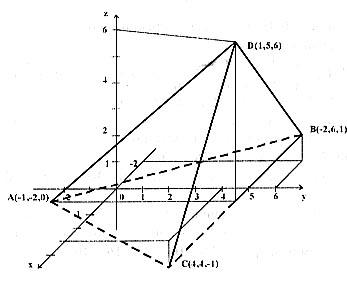
Рис. 2.

(5) Дослідження загального рівняння площини. Відп.: площина АВС паралельна вісі Оy.

(6) Нормальний вектор площини (Р) — векторний добуток напрямного вектора прямої ВС та нормального вектора площини xOy. Відп.: x + 3y = 16. Інший спосіб. Скористатися рівнянням площини, що продить через три точки D, С і С₁(4,4,0).

— нормальний вектор площини (Q); скласти рівняння площини за точкою А та вектором . Вiдп.:

(11)Очевидно, відстань між АD і BC дорівнює відстані від точки B до (Q). Відп.:

(12)

(13) — прекції точок В і С на хОy. Рівняння прямої ,

Відповідь

Інший спосіб. Оскільки то проекція – перетин площин

(Р) і xOy:

Як бачимо, параметричні рівняння можуть бути подані у різному вигляді. Пропонуємо з’ясувати, чи належить точка Е до прямої В₁С₁.

(14)

До задачі 5

Варіант 0:

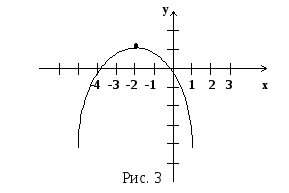
Розв’язання. а) Парабола. Рівняння перетворити до вигляду:

Точка (- 2;1) — вершина параболи. Визначити напрям віток. Для точнішої побудови лінії додатково обчислити декілька точок, наприклад, та ін. Пряма х = - 2 — вісь симетрії. Див. рис. 3.

б) Гіпербола. Канонічне рівняння

Півосі Фокуси на осі Оy. Рівняння асимптот Визначити вершини гіперболи. Використовуючи формулу додатково обчислити декілька точок лінії, наприклад, та ін. (При побудові прийняти:

) Див. Рис. 4.

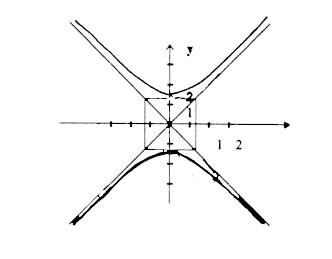
Рис. 4.

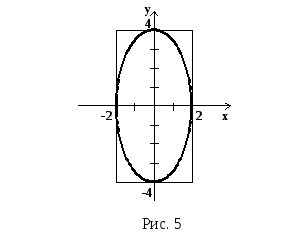
в) Еліпс. Канонічне рівняння Півосі а = 2, b = 4.Фокуси на осі Oy. Визначити вершини еліпса. Використовуючи формулу , додатково знайти декілька точок еліпса, наприклад, та ін.Див. Рис. 5.

До задачі 6

Розв’язання. а) Оскільки то рівняння зводиться до вигляду:

— еліпсоїд з центром у точці (0,3,0) і півосями а = 1, b = 4, c =1; див. Рис. 6.

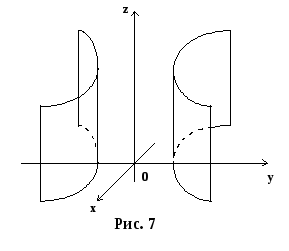
б) Гіперболічний циліндр, див. рис. 7. У площині xOy побудувати гіперболу . Поверхня, утворена твірними паралельними вісі Oz. Що проходять через дану гіперболу.

в) Гіперболічний параболоїд, див. рис. 8. Прямі UT і RS — перерізи поверхні площиною xOy. Знайти рівняння цих прямих (у площині xOy). Упевнитися, що перерізи площинами yOz і xOz — параболи APOLB і COD . Ці параболи дотикаються осей Oy і Oz. Які лінії утворюють перерізи площинами ? Визначити тип цих ліній. Довести, що перерізи площинами — гіперболи KLM , NPQ та GCH, FDE.

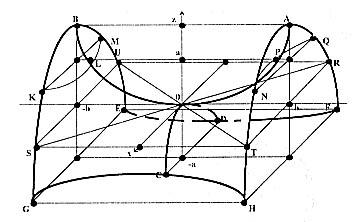
Рис.8

До задачі 7

Варiант 0:

Розв'язання. а) Тіло обмежене параболічними циліндрами

площиною , паралельною осі Ox, і площиною xOy; див. рис. 9.

б) Тіло обмежене конусом , площиною x + z = 1, паралельною осі Oy, і координатними площинами xOy (z = 0), yOz (x = 0), xOz (y = 0); див. Рис. 10. Звернути увагу нав переріз конуса площиною x + z = 1.

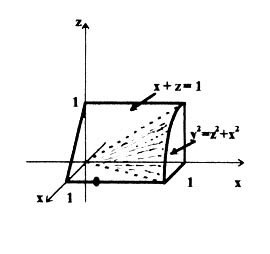Рис.10

До задачі 8

Варіант 0:

Розв’язання. а) Знайдемо для якого

Можна упевнитися, що при

Далі складемо таблицю значень

	0,6	1	1,3	1,5	1,9	...	0,3
	-10	0	10	15	30	...	150

Для задовільної побудови лінії таблиця повинна мати достатню кількість значень.

Нехай Ох — полярна вісь. Масштаб: 1 .

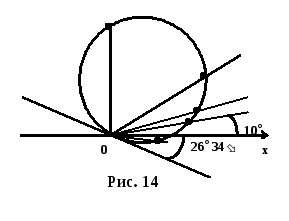
Будуємо точки лінії: на стороні кута відкладаємо 0,6 , на Ох — 1, на стороні кута і т. д. Одержані точки сполучаємо плавною лінією. Промені і дотикаються лінії у точці О. Див. мал. 14.

б) З формул переходу маємо:

Використавши ці співвідношення для перетворення рівняння

Виділяємо повні квадрати: (коло з центром у точці та радіусом ).

До задачі 9

Варіант 0:

Розв’язання. Оскільки , то

Отже ,

якщо або У зв’язку з симетрією значень косинуса, достатньо вивчити поведінку

при де, очевидно, змінюється від 1 до 0. Оскільки при то змінюється від 1 до

Складемо таблицю значень

	1	1,2	1,4	2	...
					...

Лінія симетрична відносно двох взаємно перпендикулярних прямих; див. рис. 15 (Ох — полярна вісь).

До задачі 10

Варіант 0:

Обчислення:

До задачі 11

Варіант 0:

Відп.: корені розклад на множники:

До задачі 12

Варіант 0:

Відповідь: корені

35