3.2 Теоретический раздел

3.2.1 Пересечение прямой линии с плоскостью

При решении данной задачи необходимо четко различать следующие этапы ее выполнения (алгоритм):

- проведение анализа прямой и плоскости, участвующих в пересечении, выяснить какое положение они занимают в пространстве и если общее, то выполнить построение вспомогательной плоскости дельта (), которую проводят через прямую а (а  ). В качестве вспомогательной плоскости рекомендуется брать одну из проецирующих (   ₁    ₂);

- построение линии пересечения вспомогательной плоскости дельта с заданной плоскостью сигма (n = );

- определение точки К как точки пересечения данной прямой а и построенной прямой n (аn = К)

- определение видимости прямой на плоскостях проекций.

На рисунке 3.1 дано аксонометрическое изображение прямой а, пересекающейся с плоскостью сигма, заданной треугольником АВС ((АВС)). Точка пересечения К найдена с помощью вспомогательной (горизонтально-проецирующей) плоскости дельта (₁), которая с заданной плоскостью сигма пересекается по прямой (n =   ). Искомая точка К пересечения прямой а с плоскостью треугольника определена как точка пересечения прямых а и n (К = а  n).

Рисунок 3.1

Как решается эта задача на эпюре Монжа, смотри на рисунке 3.2

Рисунок 3.2

На рисунке 3.3 рассмотрен еще один пример решения подобной задачи: определить точку пересечения прямой а с плоскостью

сигма, заданной двумя параллельными прямыми в и с (а  (в с) =К).

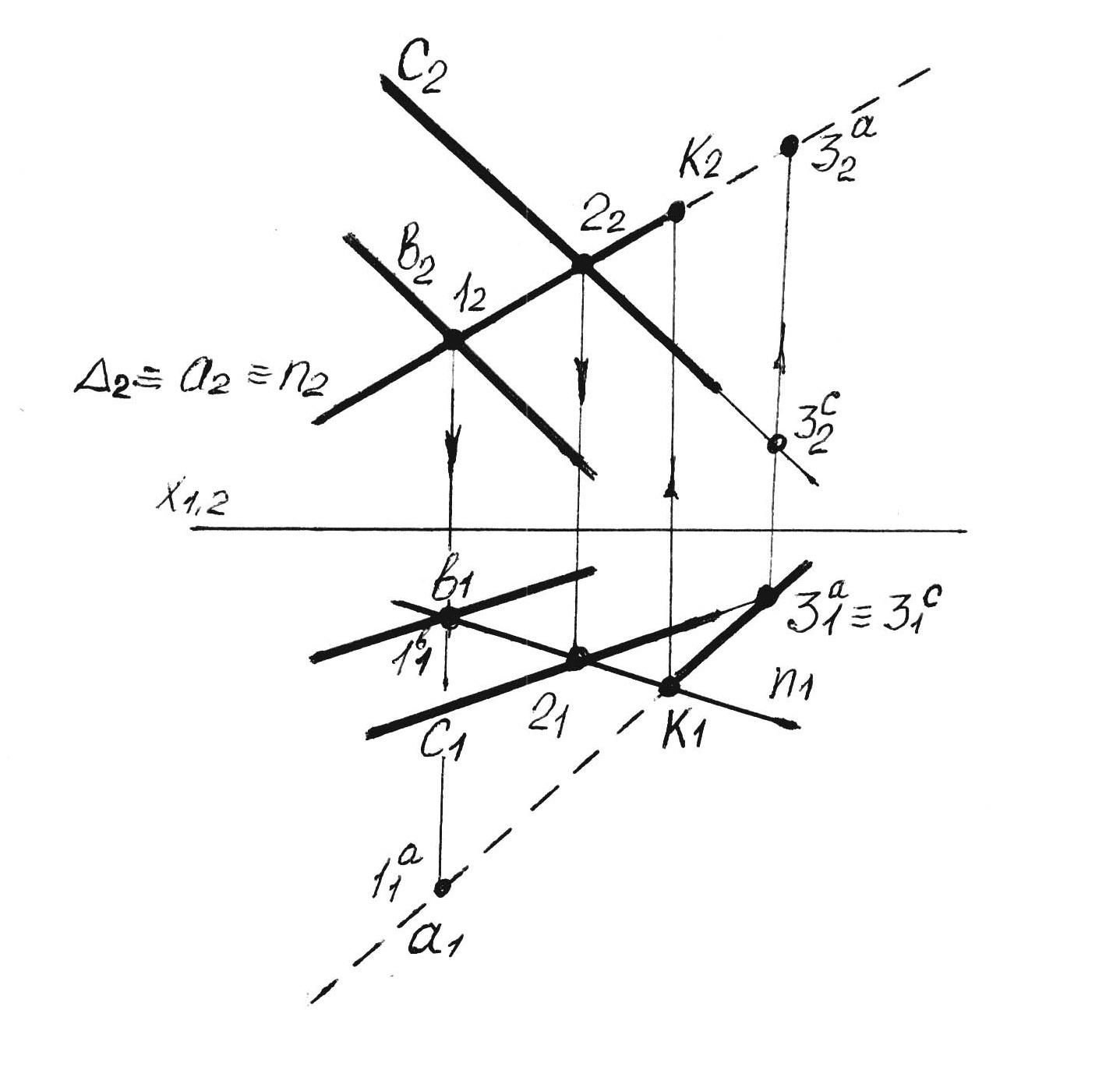
Рисунок 3.3

Порядок (алгоритм) решения данной задачи выглядит следующим образом:

- через прямую а проведем вспомогательную фронтально-проецирующую плоскость дельта (₂);

- вспомогательная плоскость дельта пересекает заданную плоскость сигма по прямой 1-2;

- находим проекции этой прямой сначала 1₂ 2₂ (1₂2₂  а₁₂ ), потом1₁ и 2₁ (точка 1 принадлежит прямой в а точка 2 прямой с, следовательно их проекции принадлежат одноименным проекциям этих прямых );

- находим точку К пересечения прямой 12 с прямой а ; 1₁2₁ а₁=К₁, К₁  К₂ (а 12) = К.

При выполнении эпюрных построений необходимо проявлять особое внимание к последней стадии решения, когда определяются проекции искомой точки.

Следует иметь в виду, что если в качестве вспомогательной секущей плоскости взята горизонтально – проецирующая плоскость, то первой из двух будет определена фронтальная проекция искомой точки (смотри рисунок 3.2). Применяя же фронтально-проецирующую плоскость, сначала находят горизонтальную проекцию К₁, а затем К₂ (смотри рисунок 3.3).

3.2.2 Определение видимости геометрических элементов способом конкурирующих точек.

Видимость для каждой плоскости проекций устанавливаем самостоятельно (рисунок 3.3). Начнем с фронтальной плоскости проекций. Рассмотрим фронтальную проекцию 1₂ точки 1. В ней как бы пересекаются прямые а и в, но они попали в одну точку на фронтальную плоскость проекций лишь потому, что в пространстве точки, принадлежащие прямым а и в находятся на одном перпендикуляре к плоскости _2. Если пройтись лучом сверху вниз, то мы увидим, что ближе к нам расположена прямая а, а прямая в за ней, следовательно, на ₂ видим сначала а₂, а потом в₂. Видимость для горизонтальной плоскости проекций устанавливаем с помощью точки 3, принадлежащей прямой а и с (). Пройдемся лучом снизу вверх и увидим, что точка 3, принадлежащая прямой с, ниже, чем точка 3 принадлежащая прямой а, следовательно, прямая а на данном участке выше и мы ее видим.

3.2.3 Пересечение двух плоскостей произвольного положения.

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, общие для обеих плоскостей, либо одну точку и направление линии пересечения двух плоскостей.

Для того чтобы определить эти точки нужно найти точки пересечения любых двух прямых одной плоскости с другой плоскостью, или точки пересечения прямой на каждой плоскости с другой плоскостью.

При решении этой задачи (вторая позиционная задача) пользуются алгоритмом, который составлен на основании общей схемы решения второй позиционной задачи. Общий вид алгоритма следующий:

- проводится вспомогательная поверхность, пересекающая заданные поверхности;

- определяется линия пересечения вспомогательной поверхности с каждой из заданных поверхностей (m и n);

- отмечают точки пересечения построенных линий, которые и являются искомыми, так как они принадлежат одновременно заданным поверхностям.

Если пересекающиеся плоскости (или одна из плоскостей) заданы многоугольниками (смотри рисунок 3.4), то построение линии их пересечения значительно упрощается если вспомогательные проецирующие плоскости провести не произвольно, а через какие- либо две из сторон многоугольников. В нашем примере вспомогательные плоскости дельта перпендикулярны горизонтальной плоскости проекций и проведены через стороны ЕD и EK, то есть решаем две задачи на пересечение прямой и плоскости (алгоритм решения этой задачи рассмотрен выше). Находим линию 12 пересечения плоскости дельта () с плоскостью треугольника АВС ((АВС) = 12). Точка М есть точка пересечения линии 12 со стороной DE (М = 12  ЕD), а точка N результат пересечения прямой ЕК с линией 34. Прямая МN является линией пересечения двух треугольников. Видимость определяем с помощью конкурирующих точек (смотри 3.2.2).

Рисунок 3.4

3.2.4 Пересечение плоскости с многогранником

Построение сечения многогранника требует многократного решения задачи о пересечении прямой с плоскостью. Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами исходного сечения. Тот же результат можно получить, сведя задачу к построению прямых пересечения плоскости с гранями тела (как пересечение двух плоскостей). Рассмотрим задачу, когда необходимо определить линию пересечения трехгранной призмы плоскостью сигма, заданной двумя пересекающимися прямыми (рисунок 3.5).

Рисунок 3.5

Каждая из вершин построенного треугольника (МNL), определена как точка пересечения соответствующего ребра, с заданной плоскостью сигма.

N = АА¹  

Для нахождения точки N проводим вспомогательную, горизонтально-проецирующую плоскость дельта, проходящую через ребро АА¹. Она пересекает плоскость  по прямой 12. Построив 1₂2₂ определяем точку N₂ и с помощью линии проекционной связи находим вторую проекцию точки N-N₁. Аналогичные построения выполняем для нахождения точек M и L.

L = ВВ¹

M = СС¹

3.3 Указания к выполнению задания (образец выполнения работы смотри в приложении Ж).

На листе формата А3, расположение книжное, по координатам точек А В и С строим комплексный чертеж плоскости сигма.

По координатам точек К,М,N и L выполняем комплексный чертеж призмы . Все построения выполняются в тонких линиях. Определяем видимость ребер призмы и сторон треугольника.

Если призму пересечь плоскостью, то в сечении получится многогранник, число вершин которого зависит от того, сколько ребер пересекает секущая плоскость. В нашем задании секущая плоскость пересекает три ребра, следовательно, в сечении получится треугольник, каждая вершина которого находится как точка пересечения ребра с плоскостью (АВС).

Р = КК¹  

R = ММ¹ 

S = NL  

Рассмотрим нахождение точки Р: через ребро КК¹ проведем вспомогательную горизонтально-проецирующую секущую плоскость дельта. Эта плоскость пересекает плоскость сигма по прямой 12, горизонтальная проекция которой совпадает с горизонтальной проекцией ребра и вспомогательной плоскости дельта (1₁2₁  К₁К'₁₂ ). С помощью проекции линии связи находим 1₂ и 2₂. Искомая точка Р находится на пересечении прямой АВ и 12 (Р=АВ 12). Точки R и S находим аналогично. По точкам Р, R, S строим треугольник , который получается при пересечении призмы плоскостью сигма, но так как плоскость сигма ограничена треугольником АВС, то и линии пересечения будут ограничены сторонами треугольника. Отмечаем эти точки D и Е , G и F и определяем видимость (приложение Ж).

Следует обратить внимание на то, что данный способ решения не является единственным. Данную задачу можно решить методом замены плоскостей проекций.