Зубенко, Омельчук - Програмування. Поглиблений курс

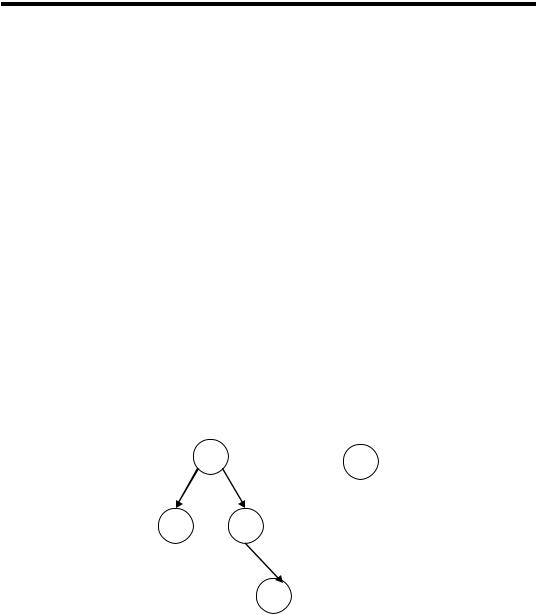
Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

(ПС2 ) Фільтр-термінатор P(x) x Σ* .

Як бачимо, не всі базові елементи термінальні. Односимвольні сло- ва за даним означенням мають вигляд pre(a,ε) ,a Σ . Побудуємо ви-

ведення слова abba в означенні ІО2 :

a,b,ε,pre(a,ε),pre(b,pre(a,ε))(= ba ),pre(b, pre(b,pre(a,ε)))(= bba ), pre(a,pre(b, pre(b,pre(a,ε))))= (abba ) .

Наведемо інше індуктивне означення (ІО2′ ) слів над Σ:

(ПС2 ) Фільтр-термінатор P (x ) x Σ* ■

Приклад 2.35. Бінарні дерева у префіксному поданні (Б-дерева) (ІО3 ). Нехай A = {a1,...,an } – сукупність вершин дерев.

(Б3 ) – порожнє Б-дерево.

(І3 ) Для вершини a A і довільних Б-дерев d1,d2 вираз a (d1,d2 ) є Б-деревом.

Бінарним деревам на рисунку за означенням ІО3 відповідають Б- дерева a (b ( , ),c ( ,d ( , ))) та a ( , ).

b с

d

■

Звернемося тепер до індуктивних означень систем множин (ІОС). Нехай P1 (x1 ),...,Pk (xk ), k ≥1, – фільтри на універсумі U , що виділя-

ють у ньому певні підмножини – сорти елементів U1,...,Uk . При цьому

221

ПРОГРАМУВАННЯ

області істинності сортових фільтрів можуть перетинатися. Індуктив- не означення системи множин M1,...,Mk має вигляд:

(БС) Фіксується певна підмножина M0 U апріорі виділених базо- вих об'єктів.

(ІС) Вибирається певна сукупність {Fi } конструкторів – операцій

на універсумі U . Конструктори за базовими й уже побудованими елементами дозволяють отримувати нові елементи універсума.

(ПС) Вибираються фільтри P1 (x ),...,Pk (x ), k ≥1, що виділяють в універсумі U сорти термінальних елементів T1,...,Tk і здійснюють від-

Приклад 2.36. КВ-мови.

Покажемо, як за допомогою ІОС можна задавати КВ-мови в дано- му алфавіті T = {a1,a2,...,an }. Нехай N = {A1,A2,...,Am } – певний алфа- віт нетерміналів. Універсум U складають натуральні числа й сукуп-

ність (T N )* усіх слів у алфавіті основних і допоміжних символів. Предикат Qi (x ), i =1,m , буде виділяти сорт слів у об'єднаному алфа- віті, що можуть бути виведені з аксіоми Ai . Розглянемо систему мов

j =1,ri . Конструктор залишає слово u без змін у разі відсутності в

ньому термінального префікса довжиною k і наступного за ним до- поміжного символу. За означенням конструктор не змінює сорт слова, тобто слово u передає у спадок новому слову vujw свій сорт.

(ПС4 ) Фільтрами є предикати Pi (x ) Qi (x )& x Σ* , i =1,m .

222

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

Нескладно перевірити, що мови Li , i =1,m , збігаються із сукупніс- тю L(Ai ) усіх слів у алфавіті Σ , що можуть бути лівосторонньо виве- дені у КВ-граматиці з правилами виведення Ai → uj , i =1,m , j =1,ri , із нетермінала Ai як аксіоми ■

2.6.2. ІНДУКТИВНІ ОЗНАЧЕННЯ ФУНКЦІЙ

Індуктивно означені функції й операції (ІОФ) визначаються на ін- дуктивних скінченно означених областях. Необхідно, щоб кожний елемент області визначення можна було розкласти на близькі до нього один або кілька елементів того самого типу. Наприклад, число n +1 розкладається на числа n та 1. ІОФ теж має базу індукції (БФ), індук- тивний перехід (ІФ) і повноту (ПФ). Розглянемо їх спочатку на при- кладі основних операцій на словах.

Операція o : Σ* × Σ* → Σ* – конкатенація слів: (БФ5 ) ε ow2 = w2 oε = w2 .

(ІФ5 ) pre(a,w1 )ow2 = pre(a,w1 ow2 ) для кожного a Σ ,w1,w2 Σ*.

Означення коректне. Воно спирається на той факт, що кожне сло- во складається з його першої літери та хвоста (слова без першої літе- ри). Дійсно, знайдемо, наприклад, значення

cb odd = pre(c,b)odd = pre(c,b odd )= pre(c,pre(b,ε)odd )= = pre(c,pre(b,ε odd ))= pre(c,pre(b,dd ))= pre(c,bdd )= cbdd .

Операція head : Σ* → Σ повертає перший символ (голову) слова, операція bottom : Σ* → Σ – останній символ слова:

(БФ6 ) head (ε)= bottom(ε)= # .

(ІФ6 ) head (aw)= a , bottom(aε)= a , bottom(aw)= bottom(w).

Операція tail : Σ* →Σ* повертає хвіст слова, тобто слово без його голови: (БФ7 ) tail(ε)= ε , (ІФ7 ) tail(aw)= w .

Операція lead : Σ* → Σ* повертає слово без останнього символу: (БФ8 ) lead (ε)= ε (ІФ8 ), lead (aε)= ε , lead (aw)= (w = ε → ε|a lead (w)).

Функція ||: Σ* → N обчислює довжину слова: (БФ9 ) |ε|= 0 , (ІФ9 ) |aw|=1+|w|.

223

ПРОГРАМУВАННЯ

Предикат p: Σ* × Σ* → Bool визначає лінійний лексикографічний порядок (нестрогий) на словах над алфавітом Σ = {a1,a2,...,an }. Нага- даємо, що символи алфавіту Σ лінійно впорядковані: ai ≤ a j i ≤ j

для 1 ≤ i, j

0 ,

= (head (u)=head (v )→ tail(u) p tail(v )|head (u) ≤ head (v )).

Наприклад, для довільних символів a,b таких, що a < b :

(ε p a ) =1,(b p ε) = 0 , (ab p ab) = (b p b) = (ε p ε) =1,

(ab p aba ) = (b p ba ) = (ε p a ) =1, (abba p aaa ) = (bba p aa ) = (b p a ) = 0 .

Нехай M = M (M0,{Fi },P ) – певна індуктивна множина зі скінчен- ними множинами твірних і конструкторів.

бір результатів означуваної функції.

Увага! Деякі аргументи в конструкторі hc можуть бути фіктивни-

ми, а за конструктор hc можна брати й саму означувану функцію f .

Найчастіше конструктор є умовним, а взагалі він може мати довільну регулярну структуру ►

224

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

∞

За лемою 2.1 M = Mi , де Mi +1 = Mi M%i , а сукупність M%i складають

i=0

H%i = {(x1,...,xm −1,c (y1,...,yn ), hc (x1,...,xm −1,y0,...,yn ,z1,...,zn )): x1,...,xm −1 M ,y1,...,yn Mi , y0 = c (y1,...,yn ),c {Fi },

(x1,...,xm −1,y1,z1 ),...,(x1,...,xm −1,yn ,zn ) Hi )}.

Такі ІОФ задають операцію множення натуральних чисел через до- давання:

(БФ) (x ×0) = 0 , (ІФ) (x ×s (y))= (x ×y) + x

і відому композицію примітивної рекурсії для n -арної натуральної функції f :

конструктора h .

Приклад 2.37. Задача про Ханойські вежі.

Є три упорядкованих кілочки, на першому з яких розташована ве- жа з n дисків, яка має вигляд конуса. За один хід можна взяти верх- ній диск із будь-якого кілочка й покласти як верхній на один із решти кілочків за умови, що на останньому не буде порушено умову конус- ності його вежі. Необхідно перенести задану вежу на другий або тре- тій кілочок. Нехай, наприклад, це буде третій кілочок.

Покладемо T = {1,2,3} – номери кілочків.

Нехай Hanoi : T ×T ×N → (T ×T )* – функція, що задає послідовність

дій із переміщення вежі висотою n з одного кілочка на інший. Для подання однієї такої дії достатньо вказати пару чисел вигляду < зві- дки, куди> , що належать T ×T . Нехай "o" – операція конкатенації двох послідовностей. ІОФ11 функції Hanoi основане на індуктивній

природі піраміди: в якому б місці її не поділити навпіл – обидві час-

225

ПРОГРАМУВАННЯ

тини будуть пірамідами, зокрема, якщо взяти її основу й ту частину, що зверху неї. Щоб перенести піраміду з кілочка x на кілочок y , до-

o (x,y) oHanoi(6 − x − y,y,n ).

Коректність ІОФ11 просто довести структурною індукцією за n

(див. вправу 15) ■ Індуктивно означені функції будемо називати просто індуктивними.

Зупинимось тепер на правилах обчислення значень індуктивних функцій. Ураховуючи, що замкнення M скінченно породжене і його конструкторів скінченна кількість, для обчислення значення індукти-

вної функції f (x1,...,xm −1,a ) можна було б послідовно будувати всі множини Hi , починаючи з H0 , доти, доки не буде побудовано пару (a, f (a )) Hn для деякого n . Однак така процедура в більшості випа-

дків буде вкрай неефективна.

Раціональніше було б не генерувати виведення всіх можливих еле- ментів замкнення, а знайти одне з виведень саме елемента a в за-

мкненні M і побудувати за ним значення b = f (x1,...,xm −1,a ) за допо- могою відповідних конструкторів. Цю побудову, у свою чергу, можна

g(x1,...,xm −1,x) і предикатів (в умовних виразах) – вони замінюються на

їхні значення, а умовні підтерми з булевими константами на місці умов

– на альтернативи. Виведення або закінчується термом tn , який не міс- тить входжень f і збігається (за побудовою) з b , або воно є нескінчен-

226

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

ним, що означає невизначеність функції f на аргументі (x1,...,xm−1,a) . Таке правило виведення називається повною підстановкою. Обчислимо

Використовують також інші правила виведення для обчислення значень індуктивної функції. Найвідоміші з них: а) правило найбільш лівої-найбільш внутрішньої заміни – виклик за значенням (замінюється тільки один найбільш лівий найбільш внутрішній виклик функції f );

б) правило найбільш лівої заміни – виклик за іменем (замінюється тіль- ки один найбільш лівий виклик функції f ) тощо. Слід мати на увазі:

якщо конструктор h умовний, то результати застосування наведених вище правил виведення можуть не збігатися (див. вправу 10).

На практиці, щоб скоротити пошук виведення елемента a , нама- гаються максимально спростити будову замкнення M . Для цього на- самперед обмежуються однозначними замиканнями. Індуктивні фун- кції в загальному випадку недетерміновані. Причина в тому, що еле-

мент індуктивної множини M = M (M0,{Fi },P ) може мати кілька сут-

тєво різних виведень з аксіом. Два виведення в M називаються екві- валентними, якщо одне з них може бути отримане з іншого переста-

новкою його членів. Індуктивна множина M = M (M0,{Fi },P ) назива-

ється однозначною, якщо в ній відсутні елементи, що мають нееквіва- лентні виведення з аксіом. Однозначність індуктивної множини гара- нтують такі три умови (але вони не є необхідними):

1) області значень будь-яких двох конструкторів c1 та c2 із {Fi } не перетинаються;

2) для кожного x M існує тільки одна сукупність гіпотез x1,...,xn така, що x = c (x1,...,xn ) для конструктора c ;

3) M0 − найменша та єдина множина твірних у M .

Умова 2) виконується для однозначних конструкторів. Якщо звер- нутися до наведених вище індуктивних означень ІО1 –ІО3 натураль-

них чисел, слів і Б-дерев, то всі вони задовольняють умови 1)–3) і тому

єоднозначними. Наступне ж означення натуральних чисел: (Б) 0 та 1 – натуральні числа,

(І) конструктор s (n ) = n +1

227

ПРОГРАМУВАННЯ

– неоднозначне. Дійсно, кожне число n > 0 за ним має два нееквіва- лентні виведення, що розпочинаються з 0 та 1. Наприклад, для 1 – це

Приклад 2.39. Обчислення ваги зваженого Б-дерева.

Нехай БДA – сукупність усіх зважених Б-дерев із вершинами з A . Індуктивна функція Wage : БДА → А задає вагу Б-дерева:

(БФ13 ) Wage( )= 0 ,

(ІФ13 ) Wage(a (d1,d2 ))= a + Wage(d1 )+ Wage(d2 ) ■

За означенням індуктивна функція f здійснює індуктивний пере-

хід тільки за одним, не обов'язково останнім, аргументом, а решта можуть розглядатися як параметри. Аналогічний вигляд мають індук- тивні означення функцій, в яких індуктивний перехід здійснюється одночасно за кількома аргументами, а також систем взаємно індук- тивних функцій. Останні особливо важливі в застосуваннях. Обме- жимося для простоти випадком бінарних функцій. У загальному ви- падку означення будуть аналогічними.

Нехай M = M (M0,{Fi },P ) – довільна індуктивна множина. Домови- мося послідовність вигляду a11,a12,...,a1m ,K, an1,an2,...,anm записувати

скорочено: aij ni,,jm=1 . Вираз aij ni,,jm=0 означає аналогічну послідовність

з індексами, що розпочинаються не з 1, а з 0, але без елемента a00 . Нехай n = n +1,m = m +1.

Загальне індуктивне означення бінарної функції f : M ×M → A має вигляд:

228

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

(ІФ) Для кожної пари конструкторів c : M n → M , d : M m → M із

сумі M ×M × A , що здійснює відбір результатів означуваної функції.

Шляхом фільтрації множини M = M (M0,{Fi },P ) можна за необхід- ності типізувати означувану функцію f . Зауважимо, що на практи- ці індуктивна функція може мати інші аргументи, за якими не здій- снюється індукція, конструктори hc,d досить прості й більшість їхніх

аргументів – фіктивні.

Приклад 2.40. ІОФ14 задає ще один варіант визначення множення

натуральних чисел через додавання з індуктивним переходом за обо- ма аргументами:

(БФ14 ) (x ×0)= (0 ×y)= 0 , (ІФ14 ) (s (x )×s (y))= x ×y + x + y +1.

Єдиним конструктором h (x1,x2,x3 ) тут є операція x1 + x2 + x3 +1`■

Увага! Кількість індуктивних переходів при обчисленні добутку x ×y в ІОФ14 збігається з величиною min{x,y} , тоді як ця величина у

випадку ІОФ з індуктивним переходом тільки за y збігається з y . З

урахуванням комутативності множення цю різницю (яка в багатьох випадках досить суттєва) можна нівелювати, помінявши попередньо місцями аргументи. Однак у загальному випадку ІОФ за кількома ар- гументами може виявитись набагато ефективнішим, ніж еквівалент- не визначення за одним аргументом ►

Як і вище, за конструктор hc,d можна брати й саму функцію f . Це

значно розширює можливості ІОФ. Наведемо один із таких прикладів. Приклад 2.41. Функції Аккермана B(x,y).

Вони відомі тим, що надзвичайно швидко зростають. (БФ15 ) B(s (x ),0)= sg (x ), B(0,y) = 2 + y .

(ІФ15 ) B(s (x ),s (y))= B(x,B(s (x ),y)).

229

ПРОГРАМУВАННЯ

В індуктивному переході (ІФ15 ) перший аргумент (x0 = s(x)) фун-

кції B ліворуч входить і в праву частину. Проте важливо, що при цьому другий аргумент у внутрішньому входженні B праворуч спро-

стився: був s (y), а став y . Аналогічно в зовнішньому входженні B

праворуч спростився перший аргумент. Це скеровує обчислення зна- чення функції до бази визначення (БФ15). Можна перевірити, напри-

клад, що B(3,1) = 2 , B(3,2)= 22 , B(3,3)= 222 тощо ■

Індуктивні означення систем функцій (ІОФС) розглянемо на при- кладі бінарних функцій типу M ×M → A . ІОФС системи бінарних фу-

нкцій [f1,K fl ],l > 0 , має структуру:

(БФС) Для x,y D0 : fk (x,y)= gk (x,y), де gk (x,y) – відома функція,

hc,d,k : M1n ×M2m ×An×m×k → A значень функції такий, що для будь-яких

x1,...,xn M1 , y1,...,ym M2 та x0 = c (x1,...,xn ) M1 , y0 = d (y1,...,ym ) M2 :

fk (c (x1,...,xn ),d (y1,...,ym ))=

=hc,d,k x0,...,xn ,y0,...,ym , f1 (xi ,y j ) ni,,jm=0 ,..., fk (xi ,y j ) ni,,jm=0 .

(ПФС) Вибираються фільтри Pk (x,y,z ), k =1,l , визначені на уні- версумі M1 ×M2 × A , що здійснюють відбір результатів означуваних функцій.

Приклад 2.42. Обчислення кількості комутативних розбиттів нату- рального числа.

Позначимо цю кількість f (n) . Тоді 1+1+1 =1+ 2 = 3 та f (3)= 3 (розбиття 1 + 2 та 2 +1 не розрізняються). Розглянемо допоміжну фун- кцію q : N ×N → N . Функція q (n,m) – це кількість комутативних роз-

230