2.8 Результати і доведення для

В цьому розділі для комплексно значної матриці , ми писатимемодля матрицьвідповідно. Використовуючи зовнішню функцію, ми визначаємо, деце повний ортонормований базистакий, що

Ми виражаємо різні проекції в термінах .

Теорема 3.1.

Покладемо w - невід’ємна інтегрована функція з . Тоді матимемо наступне:

Задовольняє умову (3.3) нижче.

Для , Теорема 3.1. дає явний вигляд. Він необхідний для проектуванняна. В силу (2.6), ми також маємо спроектуватина одновимірний підпростірабо ж визначити коєфіцієнт

де внутрішнім операторомВіповідні результати наведені в наступній теоремі.

Теорема 3.2.

Покладемо w - невід’ємна інтегрована функція з . Тоді мають місце наступні твердження:

.

Нехай . Для визначення проекціїна– мірного проміжку записів,матриціі– векторнеобхідні наступні компоненти:

Ми визначимо – мірний векторі– мірну нижню трикутну матрицю:

Так як

наступне представлення має місце:

(3.2)

де Звідси ми отримуємо

девизначено і зсунуто векторвице. В цих позначеннях, нормальне рівняння дляв теоремі 3.1 (1) буде

(3.3)

Крім того, ми визначимо . Тоді в силу (2.1), (2.8) і (2,10),

Оскільки матриця А має ранг один збурення , вона може бути легко інверсована за допомогою оберненоїі співвідношення міжіописаним в (2.1). Обернена матриця матриці А і інші відповідні результати наведені в наступній лемі.

Лема 3.3.

Доведення леми є простим, тому ми його опустимо.

Доведення теореми 3.1.

Виходячи з (3.3) ми вже вище довели (1). Використовуючи представлення в (3.2) і визначення ми маємо

Твердження (2) слідує з леми (3.3)(5),(6). нарешті, ми отримуємо (3) з (2).

Доведення теореми 3.2.

Використовуючи теорему 3.1 (2) і останню тотожність в (2.1), ми отримаємо

Звідси отримуємо (1). З (2.6) і (3.1),

Тоді (2) випливає з теореми (3.1), і (3) виводиться застосуванням теореми (3.1)(2).

Ця тотожність необхідна для доведення (4). Так

Котре, в силу (3.1) дає

Таким чином

Тепер, З іншої сторони, з (1) ми маємо:

Таким чином, ми отримуємо (4), бажану формулу відстані (2.9).

Звичайно, це являє собою великий інтерес для обчислення Для і=0– й крок проблема прогнозування була вирішена в [1], [10] з додатковою гіпотезою, що

Для всіх , де коефіцієнтивизначаються наступним чином:

Використовуючи цей результат і співвідношення двоїстості (2.4), знаходиться в [2]. Здається, цілком імовірно, що одномірний метод ортогоналізації який використовується в [2, теорема 5], може бути продовжений до, а потім за допомогою відношення двоїстості (2.4), можна також обчислити. Вздовж цього розширення набору індексівможе знадобитися припущення про місце нуліввпродовж кількох n, що піднімає питання про існування нетривіальних вагових функцій, які задовольняють ці умови.

3 Основні результати

3.1 Перевірка гіпотези про двоїстість та ортогоналізацію.

3.1.1 Приклад 1

Розглянемо спектральну щільність виду

Маємо . Звідси можемо одразу визначити коефіцієнти:

Для визначення коефіцієнтів розглянемо розклад виду

тобто перепишемо нашу щільність

Подамо у вигляді суми геометричної прогресії , звівши до відповідного вигляду отримаємо

Підставимо у праву частину рівності замість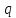

Тепер легко можна записати коефіцієнти

Перевіримо виконання умов

Тепер знайдемо стандартне відхилення для набору індексів

Для множини

Стандартне відхилення для набору матиме вигляд

3.1.2 Приклад 2

Розглянемо тепер щільність виду, а саме

де

Проведемо ту ж саму процедуру визначення коефіцієнтів і:

:

:

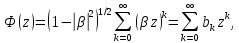
Перевіримо виконання умов

Стандартні відхилення у цьому випадку будуть

4 Висновок

В даній роботі були розглянуті основні проблеми та гіпотези задач прогнозу стаціонарних випадкових послідовностей (у широкому сенсі), спектральний розклад кореляційної функції та спектральне представлення стаціонарних регулярних послідовностей і . У роботі досліджено задачу пошуку обґрунтованої загальної індексної множини S, яка проливає світло на труднощі при обчисленні для, розглянуто два приклади застосувань теорії для гіпотез про двоїстість та ортогонлізацію, а саме дві спектральні щільності з прямим та оберненим способом відшукання коефіцієнтів ряду Фур’є, знайдено вирази для знаходження коефіцієнтівта, перевірено виконання умов регулярності, знайдено значення величин стандартних відхилень для наборів індексів.