
- •2 Теоретичні відомості
- •2.1 Стаціонарні послідовності
- •2.2 Спектральний розклад кореляційної функції
- •2.4 Спектральне представлення стаціонарних (в широкому сенсі) послідовностей
- •2.5 Регулярні послідовності
- •2.6 Екстраполяція, інтерполяція та фільтрація
- •2.7 Двоїстість та ортогоналізація
- •2.8 Результати і доведення для
- •3 Основні результати
- •5 Література
2.7 Двоїстість та ортогоналізація
Надалі
ми припускаємо, що
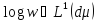 такий, що
такий, що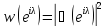 для деякої функції𝜑
з класу Харді
для деякої функції𝜑
з класу Харді
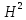 .
Нехай
.
Нехай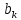 і
і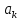 це коефіцієнти в наступних розкладах:
це коефіцієнти в наступних розкладах:
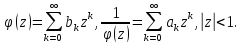
Зауважимо, що
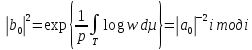
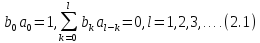
Явний
вигляд для
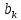 і
і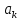 в термінах коефіцієнтів ряду Фур’є
для
в термінах коефіцієнтів ряду Фур’є
для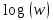 можна знайти в [11] та [12].
можна знайти в [11] та [12].
Для
набору індексів
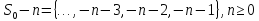 ,
котрі відповідають видаленню перших n
частот з
,
котрі відповідають видаленню перших n
частот з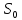 ,
відомо, що
,
відомо, що
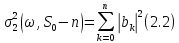
(див.
[7], [11], [2]). Це так званий
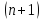 – й крок прогнозу дисперсії. Для множини
індексів
– й крок прогнозу дисперсії. Для множини
індексів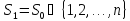 котрий дорівнює приєднанню наступних
котрий дорівнює приєднанню наступних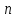 частот до
частот до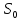 в [10] показано, що
в [10] показано, що
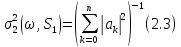
якщо
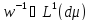 .
Дуже цікавий обернений зв'язок між
співвідношеннями (2.2) і (2.3), а також
потреба в нетривіальній умові
.
Дуже цікавий обернений зв'язок між
співвідношеннями (2.2) і (2.3), а також
потреба в нетривіальній умові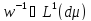 пояснюється встановленням двоїстості
між
пояснюється встановленням двоїстості
між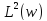 та
та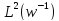 як Банахових просторів (див.
[9],
[2]). Відмітимо, що доповнення
як Банахових просторів (див.
[9],
[2]). Відмітимо, що доповнення
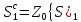 із
із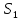 в
в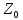 еквівалентно півосі
еквівалентно півосі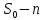 ,
де
,
де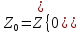 .
Отже, загальна і більш складна проблема
прогнозування на основі
.
Отже, загальна і більш складна проблема
прогнозування на основі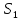 в
в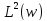 була зведена до звичайної проблеми
прогнозування в
була зведена до звичайної проблеми
прогнозування в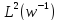 .
В цілому, для будь-якого набору індексів
.
В цілому, для будь-якого набору індексів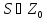 із скінченним числом точок із
із скінченним числом точок із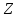 добавлених чи відібраних, нехай
добавлених чи відібраних, нехай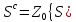 буде доповненням
буде доповненням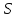 до
до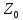 , і для фіксованого
, і для фіксованого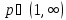 ,
визначимо
,
визначимо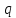 та
та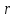 наступною рівністю:
наступною рівністю:
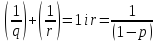
відповідно. Тоді той же аргумент двоїстості показує, що
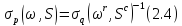
якщо
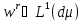 .
Хоча останнє нетривіальне обмеження
може бути послаблене [2], до
.
Хоча останнє нетривіальне обмеження
може бути послаблене [2], до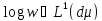 ,
але величина
,
але величина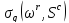 ,
можливо, не буде чітко визначена. На
щастя, для набору
,
можливо, не буде чітко визначена. На
щастя, для набору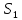 ця складність була усунута в [2, Теорема
3], використовуючи іншу задачу екстремальної
двоїстості в [3], пов’язану з проекцією
ця складність була усунута в [2, Теорема
3], використовуючи іншу задачу екстремальної
двоїстості в [3], пов’язану з проекцією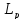 на простір Харді
на простір Харді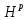 .
Тим не менш, для загального
.
Тим не менш, для загального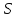 ,
визначення правої частини рівності
(2.4) залишається відкритим питанням. В
ідеалі хотілося б застосувати (2.4), коли
одна проблема простіша, ніж інша, однак
(2.4) не має сенсу, коли проблеми
прогнозування, що відповідають
,
визначення правої частини рівності
(2.4) залишається відкритим питанням. В
ідеалі хотілося б застосувати (2.4), коли
одна проблема простіша, ніж інша, однак
(2.4) не має сенсу, коли проблеми
прогнозування, що відповідають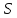 та
та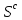 мають однакову складність або ж навіть
ідентичні. У попередньому випадку,
підходяща ортогоналізація у поєднанні
з (2.4), здається, забезпечує гарний метод
для розв’язку деяких проблем прогнозування.
Наприклад, для
мають однакову складність або ж навіть
ідентичні. У попередньому випадку,
підходяща ортогоналізація у поєднанні
з (2.4), здається, забезпечує гарний метод
для розв’язку деяких проблем прогнозування.
Наприклад, для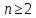 доповнення
доповнення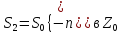 еквівалентно
еквівалентно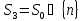 ,
що відповідає вилученню і приєднанню
одного спостереження в
,
що відповідає вилученню і приєднанню
одного спостереження в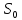 відповідно. Жодна з проблем не є
тривіальною, але останнє здається
простіше. В [2, теореми 5, 6] метод
ортогоналізації використовується для
обчислення
відповідно. Жодна з проблем не є
тривіальною, але останнє здається
простіше. В [2, теореми 5, 6] метод
ортогоналізації використовується для
обчислення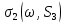 .
Тоді співвідношення двоїстості (2.4)
використовується для визначення
.
Тоді співвідношення двоїстості (2.4)
використовується для визначення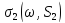 ,
що дає:
,
що дає:
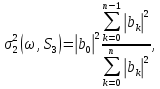
(2.5)
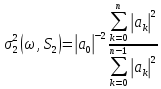
В
цьому пункті ми обчислюємо
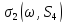 для більш загального набору індексів
для більш загального набору індексів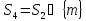 з
з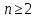 і
і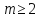 ,
тобто
,
тобто
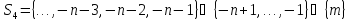
Цей
набір індексів має властивості як
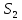 так і
так і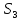 .
Насправді, він зводиться до
.
Насправді, він зводиться до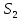 ,
коли
,
коли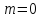 ,
в той час як його доповнення
,
в той час як його доповнення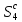 в
в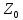 має той же вигляд, як і
має той же вигляд, як і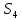 ,
так, що відношення двоїстості (2.4) не має
сенсу. Тут також показано, що метод
ортогоналізації, головним кроком якого
є визначення проекції
,
так, що відношення двоїстості (2.4) не має
сенсу. Тут також показано, що метод
ортогоналізації, головним кроком якого
є визначення проекції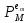 з
з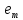 на підпростір
на підпростір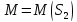 ,
може бути використаний для вирішення
проблеми. Щоби встановити значення,
позначимо ортогональну проекцію
,
може бути використаний для вирішення
проблеми. Щоби встановити значення,
позначимо ортогональну проекцію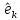 на підпростір
на підпростір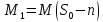 .
Оскільки
.
Оскільки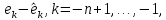 ортогональні до
ортогональні до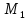 ,
то підпростори
,
то підпростори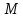 і
і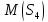 можна записати у вигляді наступних
ортогональних сум:
можна записати у вигляді наступних
ортогональних сум:
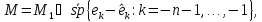
(2.6)
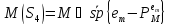
Таким
чином, обчислення
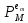 , його проекції та норми являється
першочерговим. Наступна тотожність,
яка являє собою узагальнення [2, теорема
6], представляє окремий інтерес. Власне
, цікавий її зв’язок з
, його проекції та норми являється
першочерговим. Наступна тотожність,
яка являє собою узагальнення [2, теорема
6], представляє окремий інтерес. Власне
, цікавий її зв’язок з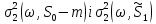 ,
де
,
де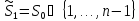 (з
(з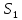 ,
де
,
де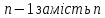 ):
):
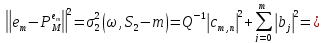
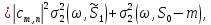 (2.7)
(2.7)
Де
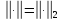 i
i
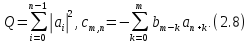
Константа
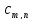 насправді являється коефіцієнтом
насправді являється коефіцієнтом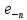 у формальному розкладі в ряд
у формальному розкладі в ряд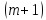 -го
кроку прогнозу
-го
кроку прогнозу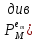 .
[16]).
Наостанок, бажана відстань:
.
[16]).
Наостанок, бажана відстань:
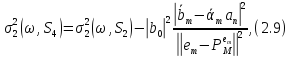
Де
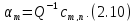
На
відміну від (2.2), (2.3) і (2.5), де відстань
залежить або ж лише від
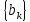 або лише від
або лише від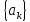 ,
у випадку (2.7) і (2.9) одночасно залежить
від обох. Явні вирази цих відстаней
забезпечують корисні інструменти для
оцінки впливу додавання (вилучення)
вектора на зниження (підвищення) таких
відстаней. А саме, як слідує з (2.7),
видалення
,
у випадку (2.7) і (2.9) одночасно залежить
від обох. Явні вирази цих відстаней
забезпечують корисні інструменти для
оцінки впливу додавання (вилучення)
вектора на зниження (підвищення) таких
відстаней. А саме, як слідує з (2.7),
видалення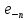 із
із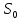 не буде збільшувати відстань від
не буде збільшувати відстань від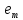 з
з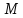 якщо
якщо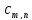 рівне нулю. Аналогічно з (2.9), додавання
рівне нулю. Аналогічно з (2.9), додавання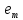 до
до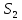 не зменшить
не зменшить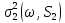 якщо
якщо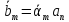 .
Ці факти швидше за все мають цікаву
інтерпретацію результатів у статистиці
(див. [16], [14]). Було б корисно привести
кілька конкретних прикладів оціночних
функцій
.
Ці факти швидше за все мають цікаву
інтерпретацію результатів у статистиці
(див. [16], [14]). Було б корисно привести
кілька конкретних прикладів оціночних
функцій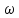 або ж стаціонарних процесів, які
відображають ці феномени.
або ж стаціонарних процесів, які
відображають ці феномени.
