Зміст

1 Вступ 2

2 Теоретичні відомості 3

2.1 Стаціонарні послідовності 3

2.2 Спектральний розклад кореляційної функції 4

2.4 Спектральне представлення стаціонарних (в широкому сенсі) послідовностей 5

2.5 Регулярні послідовності 6

2.6 Екстраполяція, інтерполяція та фільтрація 7

2.7 Двоїстість та ортогоналізація 10

2.8 результати і доведення для 14

3 Основні результати 20

3.1 Перевірка гіпотези про двоїстість та ортогоналізацію. 20

3.1.1 Приклад 1 20

3.1.2 Приклад 2 22

4 Висновок 24

5 Література 25

1 Вступ

Багато прогнозувальних задач стаціонарних випадкових процесів (див. [2], [7], [10], [14]) еквівалентні пошуку відстані від сталої функції 1 до підпростору в ,де S – підмножина цілих чисел , e_k = e^-ikλ, w-невід’ємна інтегрована функція на одиничному крузі T, і це зважений простір на T з нормою 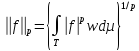.Тут µ - це Лебегова міра на Т, причому µ(T) = 1. Записуємо

для відстані. Наприклад, складається із многочленів , і їх границь в коли індексна множина S, є пів пряма , тобто

У цьому випадку, загальновідома теорема стверджує, що для ,

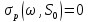якщо ; в іншому випадку (див., наприклад, [5, p. 156]). У праці [10] для індексної множини привернула значну увагу до обчислення коли індексна множина єз обмеженою кількістю доданих та видалених точок. На сьогодні, найбільш відомий загальний результат – це Теорема 2 Ченга та ін., яка стверджує, що, для такого, є позитивним лише за умови що Однак, задача обчислення та функції в ,що його досягає, залишається недосяжною, навіть якщо , , за винятком кількох особливих випадків, розглянутих у пункті 2. У цій роботі ми розв’язуємо задачу пошуку обґрунтованої загальної індексної множини S, що могла б пролити світло на труднощі, звичайні для цієї сфери досліджень. Пункт 3 представляє результати дляі містить деякі відкриті питання щодо загального .

2 Теоретичні відомості

2.1 Стаціонарні послідовності

Нехай – ймовірнісний простір і - деяка послідовність випадкових величин. Позначимо черезпослідовність

Означення 1.

Випадкова послідовність називається стаціонарною (у вузькому сенсі), якщо для любого розподіли ймовірностей співпадають:

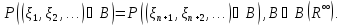
Означення 2.

Послідовність комплексних випадкових величин з ,, називається стаціонарною (в широкому сенсі), якщо для всіх

Позначимо

І припускаючи, що

Функцію будемо називати коваріаційною функцією, а– кореляційною функцією стаціонарної (в широкому сенсі) випадкової послідовності.

2.2 Спектральний розклад кореляційної функції

Нехай

де - ортогональні випадкові величини з нульовими середніми і . Якщо покласти, що , то рядсходиться в середньоквадратичному сенсі і

Введемо функцію

Тоді коваріаційна функція може бути записана у вигляді інтеграла Лебега-Стілт’єса

Теорема (Герглотц).

Нехай – коваріаційна функція стаціонарної (в широкому сенсі) випадкової послідовності з нульовим середнім. Тоді на знайдеться така скінченна міра ,

, що для любого

де інтеграл розуміється як інтеграл Лебега-Стілт’єса по множині.

2.4 Спектральне представлення стаціонарних (в широкому сенсі) послідовностей

Теорема 1.

Існує така ортогональні стохастична міра , що для кожного (-м.н.)

При цьому .

Теорема 2.

Якщо , то знайдеться така функція , що (-м.н.)

2.5 Регулярні послідовності

Введемо позначення. Нехай та – замкнені лінійні многовиди, породжені величинами івідповідно. Нехай також

Означення.

Стаціонарна послідовністьназивається регулярною, якщо

і сингулярною, якщо

Теорема.

Кожна стаціонарна в широкому сенсі випадкова послідовність допускає єдиний розклад

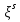де – регулярна, а – сингулярна послідовності. При цьому іортогональні (.

Означення.

Клас Харді – це клас аналітичних функційу відкритому одиничному коліна комплексній площин, які задовольняють умову

Теорема (Колмагоров).

Нехай – не вироджена регулярна стаціонарна послідовність. Тоді існує спектральна щільністьтака, що

А саме, (майже скрізь по мірі Лебега).

І навпаки, якщо – деяка стаціонарна послідовність, що має спектральну щільність, яка задовольняє умову (1), то ця послідовність є регулярною.

2.6 Екстраполяція, інтерполяція та фільтрація

Екстраполяція.

Розглянемо частковий випадок, коли спектральна щільність задається у вигляді

де функція має радіус збіжності і не має нулів в радіусі

Нехай

– спектральне представлення послідовності .

Теорема 1. Якщо спектральна щільність послідовності може бути представлена у вигляді (1), то оптимальна (лінійна) оцінкавеличинипозадається формулою

де

та

Інтерполяція.

Найпростішою задачею інтерполяції є задача побудови оптимальної (в середньоквадратичному сенсі) лінійної оцінки по результатам спостережень «пропущеного» значення .

Позначимо через – замкнений лінійний многовид, породжений величинами. Тоді кожна випадкова величинаможе бути представлена у вигляді

де належить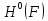 замкненому лінійному многовиду, породженому функціями і оцінка

буде оптимальною тоді і тільки тоді, коли

Із властивостей «перпендикулярів» в гільбертовому просторі випливає, що функціяповністю визначається двома умовами:

1. 

2. 

Теорема 2 (Колмагоров).

Нехай – регулярна послідовність з

Тоді

де

І похибка інтерполяції задається формулою

Фільтрація.

Задача фільтрації полягає в побудові оптимальної ( в середньоквадратичному сенсі) лінійної оцінки величини по тім чи іншим спостереженням послідовності

Оскільки , то знайдеться така функція, що

Оптимальна функція :

1. ,

2. .

Отриманий розв’язок (4) можна використати для побудови оптимальної оцінки величини по результатам спостережень, де – деяке задане число з .