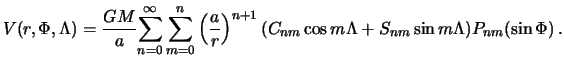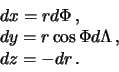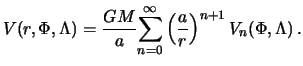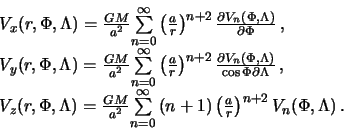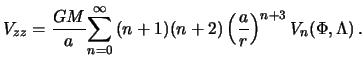7.4 Вторые производные потенциала притяжения в околоземном пространстве

Как мы уже говорили, главным препятствием для измерения силы тяжести на борту космического аппарата служит невесомость. Однако существует принципиальная возможность измерять элементы тензора вторых производных потенциала.

Пусть точка есть точка, совпадающая с центром масс космического аппарата. Выберем прямоугольную систему координат, связанную с космическим аппаратом (сопровождающий трехгранник). Начало этой системы координат возьмем в точке. Направления осей выберем следующим образом: осьPx направим по касательной к меридиану, проходящему через точку , осьPy -- на восток, а ось Pz -- в начало сферической системы координат, то есть в центр Земли. Пусть -- радиус-вектор точки,и-- соответственно геоцентрическая широта и долгота этой точки. Тогда потенциал притяжения в этой точке будет равен

(7.16)

Здесь и-- стоксовы постоянные. В данном случае мы центробежный член не учитываем, так как речь идет о потенциале гравитационного притяжения, а не тяжести.

Элементарные приращения декартовых координат, очевидно будут

(7.17)

Первые производные гравитационного потенциала по осям сопровождающего трехгранника можно записать в виде дифференциального оператора

(7.18)

Обозначим

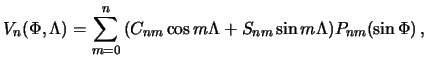
теперь формулу (7.16) можно переписать так

(7.19)

Подставляя полученную формулу в (7.18), будем иметь компоненты градиента потенциала притяжения на расстоянииот центра Земли

(7.20)

Чтобы получить вторые производные потенциала притяжения, необходимо каждую из компонент силы притяжения продифференцировать по трем координатным осям. При вычислении вторых производных нельзя пользоваться формулами линейной связи элементарных приращений координат (7.17), как мы это делали при вычислении первых производных. Самый очевидный путь (но не самый легкий!) -- прямое дифференцирование функциикак неявную функцию переменных. Однако он связан с громоздкими выкладками.

Наша цель -- показать как изменяются вторые производные потенциала с увеличением расстояния до спутника. Поэтому ограничимся лишь второй радиальной производной потенциала. Силовая линия для этой координаты -- прямая линия, поэтому учитывать ее кривизну не требуется. Дифференцируя потенциал, заданный формулой (7.19), по координате, получим

(7.21)

Мы видим, что после дифференцирования каждый член разложения потенциала приобретает коэффициент, растущий с увеличением степени как Таким образом, множительуказывает, что с повышением "частоты" увеличивается и множитель, точно так же, как и при спектральном разложении функции времени. Таким образом, дифференцирующий эффект увеличивает "верхние" гармоники разложения потенциала.

Однако, одновременно с этим эффектом существует и "интегрирующий" эффект: с увеличением расстояния множительуменьшает амплитуду гармоники. Поэтому возникает вопрос, какие гармоники и на какой высоте следует определять при планировании космического эксперимента.

Английский ученый Каула экспериментально показал, что амплитуды сферических гармоник потенциала убывают с возрастанием степени как. С другой стороны амплитуды гармоник второй производной потенциала увеличиваются как. Следовательно гармоники вторых производных в широком диапазоне частот имеют характер "белого шума". Но с увеличением высоты благодаря интегральному эффекту верхний диапазон частот оказывается подавленным.

Выполним простейший расчет "частотной характеристики" преобразования сферических гармоник потенциала в гармоники радиальной второй производной на высоте .

Пусть , где-- высота полета спутника над планетой. В качестве характеристики подавления гармоники степени, очевидно, можно принять

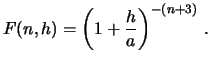
Приведем таблицу значений при различных высотах и степеней гармоник.

h	200 км	500 км	1000 км	5000 км
n
2	0.86	0.68	0.48	0.055
4	0.80	0.59	0.36	0.017
6	0.76	0.51	0.27	0.005
8	0.71	0.44	0.20	-
10	0.67	0.37	0.15	-
20	0.49	0.18	0.035	-
50	0.19	0.018	--	-
100	0.041	--	--	-

Таблица показывает, что для выполнения задачи измерения вторых производных годятся лишь очень низкие спутники. Причем на высоте 200 км от гармоник степени и порядка 100 остается лишь около 4%. Это означает, что если на поверхности Земли нас может удовлетворить точность 1% от амплитуды аномалий градиента, то в космических условиях мы будем вынуждены требовать точность на два порядка выше. Следовательно, в качестве приемлемой точности измерения мы должны планировать чувствительность приборов не менее 0,001Э, что эквивалентно градиенту мГал/м  g/м. Такой высокой чувствительности в земных условиях вряд ли можно достигнуть. Однако в космосе, в условиях глубокого вакуума и сверхнизких температурах надежда на успех остается.