Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4604 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Башкирский Государственный Педагогический Университет им. М. Акмуллы
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Координатно-векторный метод 3

.pdf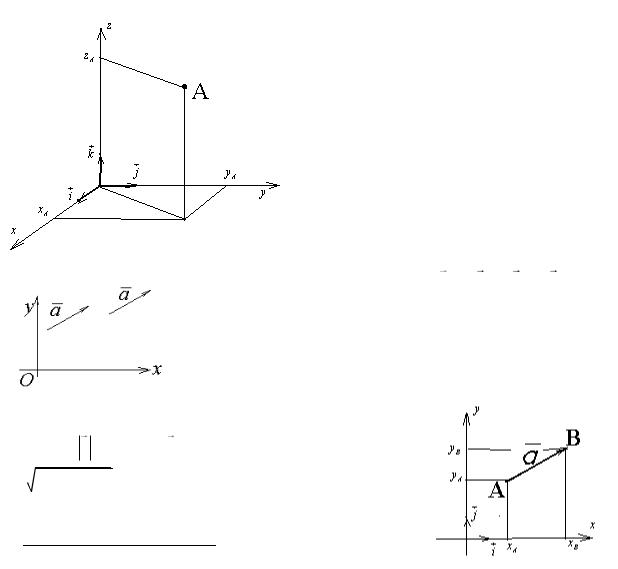
Скачиваний:
16
Добавлен:
07.03.2016
Размер:
484.97 Кб
Скачать
☆

1

Шведова И.Г., учитель математики лицея №1580

Векторные методы решения задач по стереометрии

Применение векторной алгебры в школьном курсе геометрии в настоящее время в большинстве случаев ограничивается решением задач чисто векторного содержания. Речь идет о задачах типа « найти площадь треугольника с вершинами A(1;1;1), B(2;3;4), C(4;3;2) »1 и подобных. В стереометрии

векторные методы иногда используют для нахождения различного вида углов в прямоугольном параллелепипеде. И, что интересно, теоретический материал по данной тематике в учебниках излагается довольно подробно, вплоть до способов вычисления координат векторного произведения векторов, его главных свойств и основ аналитической геометрии. Таким образом, по существу, невостребованным остается пласт знаний, достойный широкого применения в решении ряда сложных стереометрических задач. Целью настоящей заметки является показать читателю, насколько выигрышным может быть использование векторных приемов на практике. Начнем с краткого описания основного «инструментария».

Азбука векторов

Координаты точки A(xA ; yA ; zA ) в декарто-

вой (прямоугольной) системе координат Oxyz представляют собой проекции точки на координатные оси.

Векторы однозначно определяются своими координатами

ax xB xA ; ay yB yA ; az zB zA a ax i ay j az k (ax ; ay ; az ) ,

то есть являются свободными .

Длина a вектора a вычисляется по формуле

ax2 ay2 az2 .

1 Геометрия. 11 кл. Е.В.Потоскуев, Л.И.Звавич.

2

Скалярное произведение векторов есть число a b = a b cos axbx ayby azbz .

Угол между векторами вычисляется по формуле cos

a

 

b

.

a

 

b

 

 

 

 

 

 

 

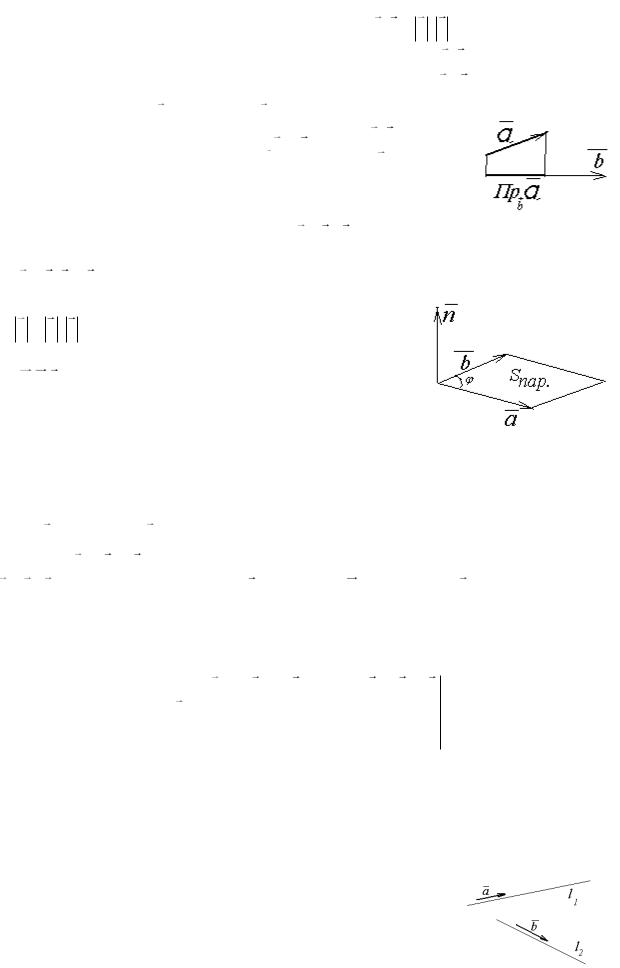
Проекция вектора a на вектор b вычисляется в соответ-

ствии с рисунком по формуле Пр a

 

a

 

cos

a

 

b

.

 

 

 

 

 

 

 

b

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Векторное произведение векторов n a b есть вектор, удовлетворяющий трем условиям:

1)n a; n b ,

2)n a b sin Sï àð.

3)a, b, n образуют правую тройку векторов.

Для решения задач используются свойства 1) и 2).

Координаты векторного произведения удобно вычислять через определи-

тель.

Если a (ax ; ay ; az ) , b (bx ;by ;bz ) , то

 

i

j

k

 

n a b

ax

ay

az

(aybz azby ) i (axbz azbx ) j (axby aybx ) k .

 

bx

by

bz

 

для вычисления определителя удобно использовать вынесение общего множителя строки или столбца за знак определителя.

 

i

j

k

 

i

j

k

n

kax

kay

kaz

k m

ax

ay

az

 

mbx

mby

mbz

 

bx

by

bz

 

 

 

 

 

 

 

 

Теоретические задачи

1. Нахождение углов

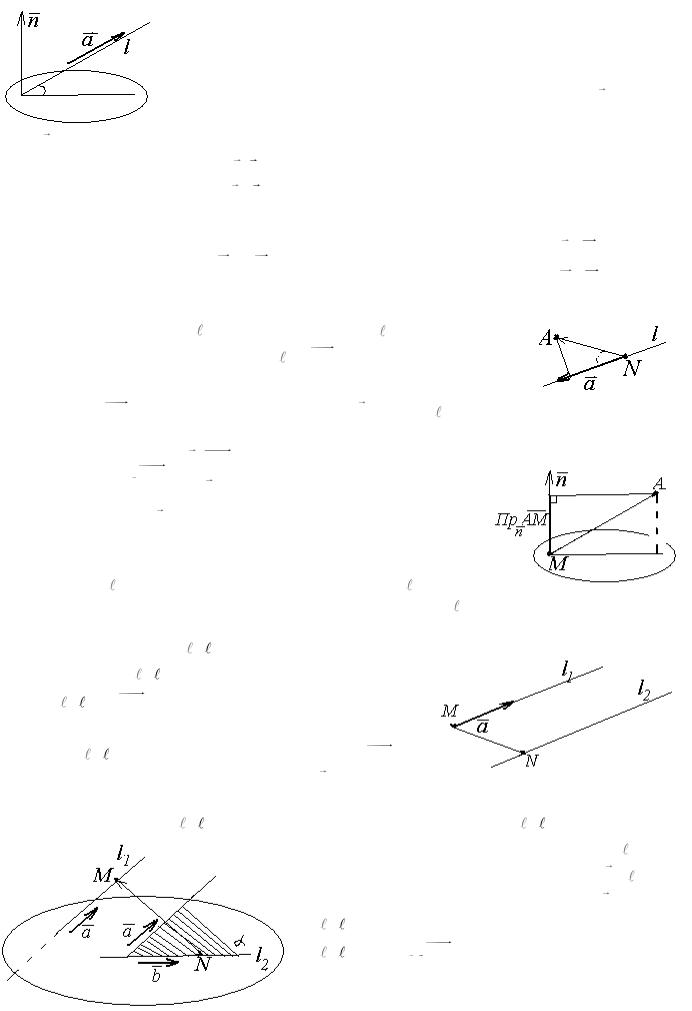
а) Между прямыми.

Прямая в пространстве однозначно задается точкой и направляющим вектором (вектором параллельным прямой). Угол между прямыми вычисляется как острый угол между направляющими векторами прямых.

3

б) Угол между прямой и плоскостью определяется как угол между прямой и ее проекцией на плоскость. Для нахождения этого угла используется угол между направляющим a вектором прямой и нормальным (перпендикулярным) вектором

n плоскости. При этом синус угла между прямой и плоскостью определя-

ется по формуле: sin

 

a n

 

 

 

 

 

 

 

 

a

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) Угол между плоскостями вычисляется как острый угол между нор-

мальными векторами n

и n этих плоскостей по формуле cos

 

 

n1 n2

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

n1

 

n2

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Нахождение расстояний

 

 

 

 

 

 

 

а) Расстояние ( A, ) точки А до прямой в пространстве

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

вычисляется по формуле ( A, )

AN

sin .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Здесь N- произвольная точка на прямой, -угол между век-

торами AN и направляющим вектором a прямой .

б) Расстояние ( A, ) от точки А до плоскости вычисляется по формуле

 

 

 

 

 

n AM

 

. Здесь М- произвольная точ-

 

 

 

( A, ) =

Пр AM

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ка плоскости, n - нормальный вектор плоскости.

 

 

 

 

По этой же формуле вычисляется расстояние от

 

 

 

прямой

до плоскости , которой прямая

парал-

 

 

 

лельна. При этом А- произвольная точка прямой

, М- произвольная точка

плоскости .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) Расстояние ( 1, 2 ) между параллельными

 

 

 

 

прямыми

1, 2

 

 

вычисляется

по

 

формуле

 

 

 

 

( 1,

2 )

MN

sin .

 

Здесь

М,

 

N

–

 

 

 

 

соответственно произвольные точки на пря-

 

 

 

 

мых

1, 2 , а -

угол между вектором MN и

 

 

 

 

общим направляющим вектором a

этих пря-

 

 

 

 

мых.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

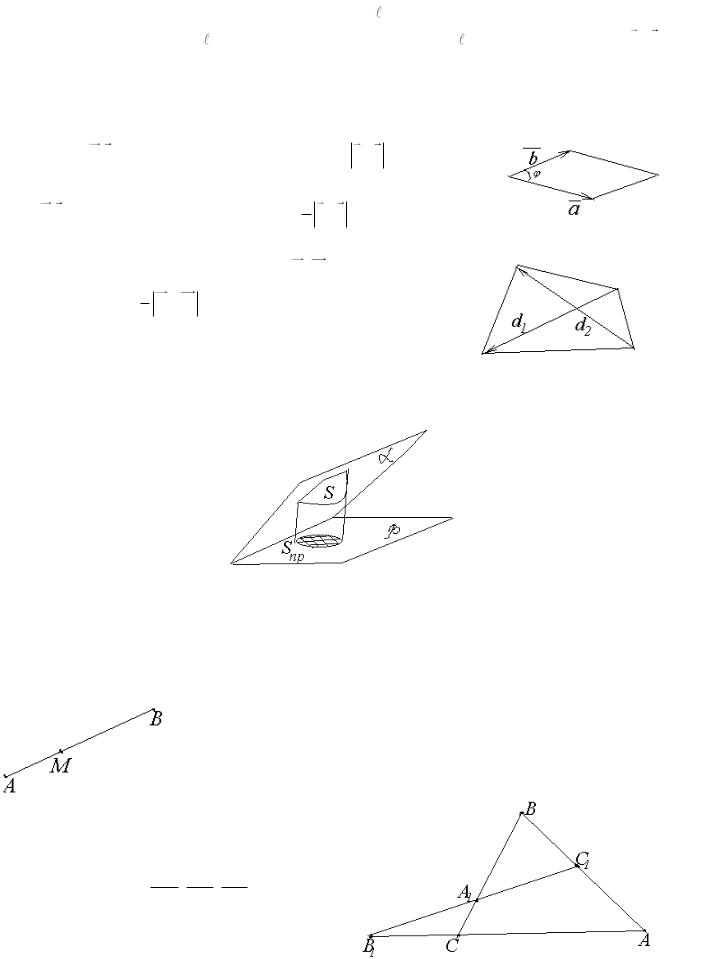
г) Расстояние (

1,

2 ) между скрещивающимися прямыми

1, 2 , которые за-

 

 

 

 

 

 

 

 

 

 

 

 

даются в пространстве соответственно:

1 -

 

 

 

 

 

 

 

 

 

 

 

 

точкой М и направляющим вектором a ;

2 -

 

 

 

 

 

 

 

 

 

 

 

 

точкой N и направляющим вектором b .

 

 

 

 

 

 

 

 

 

 

 

 

 

(

1,

2 )

 

вычисляется

по

формуле

 

 

 

 

 

 

 

 

 

 

 

 

(

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1,

2 ) =

Прa b MN

.

Происхождение

этой

 

 

 

 

 

 

 

 

 

 

 

 

формулы объясняется следующим образом.

 

 

 

 

 

 

 

 

 

 

 

 

Расстояние

между

скрещивающимися

пря-

 

 

4

мыми – суть расстояние от одной из них

1

до плоскости , проходящей че-

 

 

рез другую прямую 2 параллельно первой прямой 1 . При этом вектор a b является нормальным для плоскости .

3. Вычисление площадей

а) Площадь S параллелограмма, построенного на век-

торах a, b вычисляется по формуле: S a b

б) Площадь треугольника, построенного на векторах a, b вычисляется по формуле S 12 a b .

в) Площадь произвольного выпуклого плоского четы-

рехугольника с диагоналями d1, d2 вычисляется по формуле S 12 d1 d2 .

г) Площадь Sпр проекции на плоскость произволь-

ной фигуры, лежащей в плоскости и имеющей площадь S , вычисляется по

формуле Sпр S cos . Здесь -угол между плоскостями , .

Формула деления отрезка в данном отношении.

Пусть точка М делит отрезок АМ в отношении .

 

AM

 

 

. Тогда x

 

xA xB

; y

M

 

yA yB

; z

M

 

zA zB

.

 

 

 

 

 

 

 

 

 

 

MB

 

 

M

 

1

 

1

1

 

 

 

 

 

 

 

 

 

Теорема Менелая

В любом треугольнике АВС имеет ме-

сто равенство AC1 BA1 CB1 1.

C1B A1C B1 A

5

Рассмотрим решения нескольких задач из разряда «олимпиадных», в основу которых положены сведения, приведенные выше.

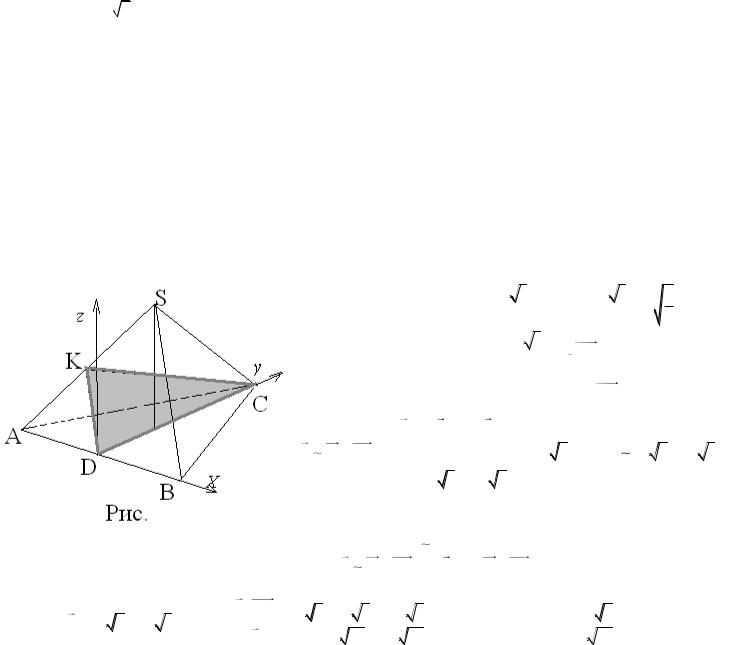
1. В правильной треугольной пирамиде SABC со стороной a и боковым ребром a 3 плоскость проходит через высоту основания. Вычислите площадь наименьшего сечения пирамиды этой плоскостью.

Решение.

Сечение пирамиды плоскостью представляет собой треугольник DСК, вершина К которого лежит на ребре AS. Наименьшее значение площади этого треугольника соответствует случаю, когда его высота, опущенная из точки К, является расстоянием между скрещивающимися прямыми DC и AS, то

есть

равно

( AS, DC) . Введем

систему

координат

с центром в точке D,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A(

a

;0;0), B(

a

;0;0), C(0;

 

a

3

;0),

S(0;

 

a

3

;2 a

 

 

2) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

6

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

min

 

DC ( AS, DC) . S

1

 

a 3

 

Пр AD

 

.

 

 

 

 

Здесь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

AD (

a

; 0; 0)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

( j AS)

 

0

 

 

 

1

0

 

 

 

 

(4a

6; 0; 3a)

(4

2; 0; 3),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3a a 3 4a

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Здесь значок « » использован для обозначения

коллинеарности векторов, то есть n

 

 

( j AS) n k ( j AS), k R.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n AD

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

3

 

 

2a

 

 

2

 

a2 6

.

 

 

 

 

 

Ответ:

 

6

 

.

 

 

 

 

 

 

 

 

 

n (4

 

2;0;

3). Smin

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

35

2

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

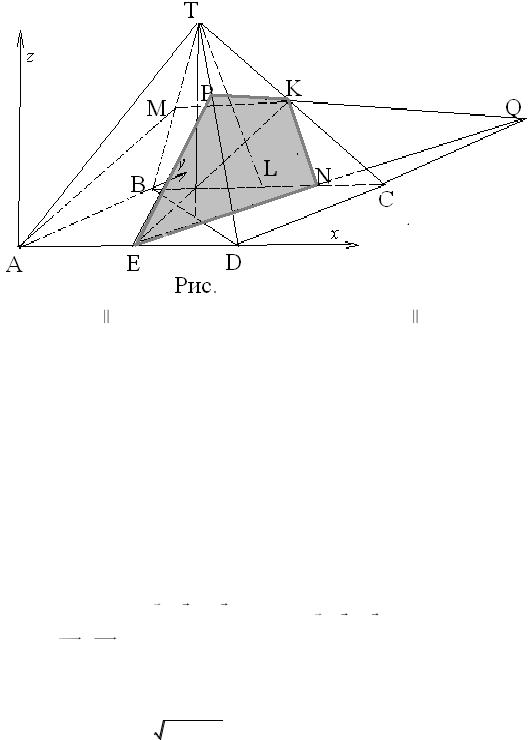
2. Найдите площадь сечения правильной четырехугольной пирамиды ТАВСD плоскостью, параллельной апофеме ТL боковой грани ТВС и медиане АМ боковой грани ТАВ и проходящей через середину бокового ребра TC, если сторона основания пирамиды равна 8, а расстояние от вершины пирамиды до секущей плоскости равно 40/21.

Решение.

Построим сечение пирамиды плоскостью :

пл.AMK :

KE

AM , KE AM AE

1

AD, пл.BTC :

 

 

KN

 

 

TL, KN

1

 

TL ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

пл.ABC :

EN DC Q пл.DTC DTC QP, EPKN искомое сечение.

Запишем

 

 

координаты

 

 

точек:

 

 

 

 

A(0;0;0), T (4; 4; h), C(8;8;0), E(4;0;0), D(8;0;0),

N (6;8; 0), K (6;6;

h

) . Для расчета

координат точки Р применим теорему Мене-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

лая

для

треугольника

DTC:

 

DP

 

 

TK

 

 

CQ

1

 

DP

1

1

1

DP

2 . Используя

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PT

 

 

 

 

KC QD

 

 

 

PT

 

 

2

 

 

 

PT

 

формулы

 

 

деления

 

 

 

отрезка

 

 

 

 

 

 

в

 

 

данном

 

 

 

 

 

отношении,

полу-

чим: x

 

 

xD 2xT

 

 

16

, y

 

 

yD 2 yT

 

 

8

, z

 

 

 

 

2

h . P(

16

;

8

;

2h

) . Запишем формулу

 

 

 

 

P

 

 

 

 

P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

1 2

3

 

 

 

 

 

3

 

 

 

 

3

 

 

 

 

 

3

 

 

 

 

 

3

 

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

для площади сечения:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

j

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

j

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

h

 

 

1

 

 

 

 

1

 

 

2

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

сеч.

 

 

 

EK PN

 

 

 

2

 

 

6

 

 

 

 

 

 

 

4

 

12

h

 

 

 

(20h;5h; 20)

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2 2 3

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 8 h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

16

 

 

2h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

3

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Sсеч.

 

 

 

(4h; h; 4)

 

 

 

17h2 16 .

Для

 

 

 

нахождения

 

 

h

 

используем

условие:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

40

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(T , )

.

В

 

 

то

 

 

же

время

(T , )

можно

 

представить

в виде

 

 

 

 

 

 

 

 

 

 

 

 

21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7

 

 

 

 

 

 

 

 

40

 

 

 

 

 

 

 

 

h

 

5

 

(T , )

 

Пр TE

 

,

n ( 4h; h;4),

TE (0;4; h)

 

 

 

n TE

 

 

 

 

. Отсю-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

21

 

 

 

n

 

 

 

17h2 16

21

да h2 25 S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

35

.

 

 

 

 

 

 

 

 

 

 

 

 

сеч.

 

 

2517 16

 

 

 

 

 

 

 

 

 

 

 

 

6

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: Sсеч. 17,5

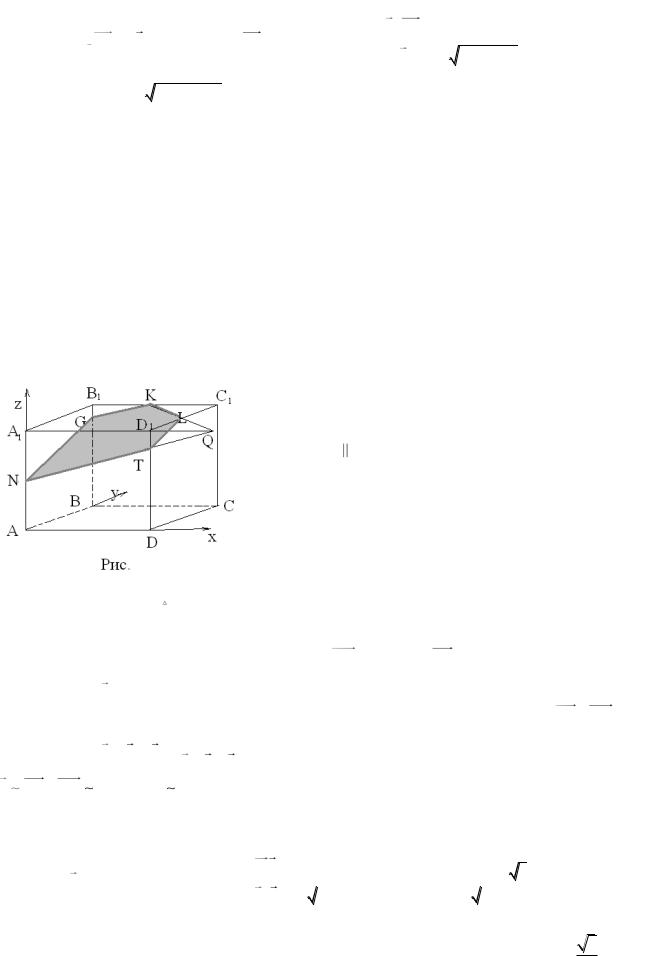
3. В кубе АВСВА1В1С1D1 со стороной a точка К является серединой стороны верхнего основания В1С1, точка L делит другую сторону С1D1 этого основания в отношении 2:1, считая от вершины С1 , точка N является серединой бокового ребра АА1. Найдите площадь сечения, проходящего через точки К,

L, N.

Решение:

Построим сечение куба через точки K, L, N.

 

 

 

 

 

 

 

пл.A1B1C1 : KL A1D1 Q, пл.AA1D1 : NQ DD1 T

 

 

 

 

 

 

 

пл.BB1C : KG TN, NTLKG

 

- искомое

сечение.

 

 

 

 

 

 

 

Площадь сечения

 

вычислим, используя фор-

 

 

 

 

 

 

 

мулу

Sпр S cos ,

где

- угол между нор-

 

 

 

 

 

 

 

мальными

векторами

плоскости

основания

 

 

 

 

 

 

 

куба и плоскости сечения. Площадь проекции

 

 

 

 

 

 

 

сечения куба на плоскость АВС можно вы-

числить как S

 

S

 

=

a2

1

KC C L a2

 

1

 

1

 

2

a2

5

a2 . В декартовой си-

ABCD

KLC

 

 

 

 

 

 

 

 

2

1

1

2

2

 

3

 

6

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

стеме координат с центром в вершине куба А координаты вершин имеют

вид: K (

a

; a; a), L(a;

 

a

; a), N (0; 0;

a

) .

 

Отсюда

NK (

a

; a;

a

), NL (a;

 

a

;

 

a

) . Нормаль-

2

 

 

3

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

3

 

 

2

 

 

 

ный вектор n

сечения можно принять пропорциональным (коллинеарным)

векторному

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

произведению

 

 

 

 

 

 

 

 

 

 

 

 

 

 

NL NK .

 

 

 

i

 

j

 

k

 

 

i

j

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n NL NK

1

 

 

 

 

6

2 3

(4; 3;10) . Нормальный вектор плоскости ос-

 

 

 

 

 

 

 

 

3

2

 

 

 

 

 

 

1

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n k

 

 

 

 

 

 

Sпр

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

нования k (0;0;1) . Тогда cos

 

 

 

 

10

 

и S

 

 

5

a2

10

 

 

 

 

 

5

a2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

k

 

5 5

 

 

cos

6

 

5 5

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 35 a2 .

8

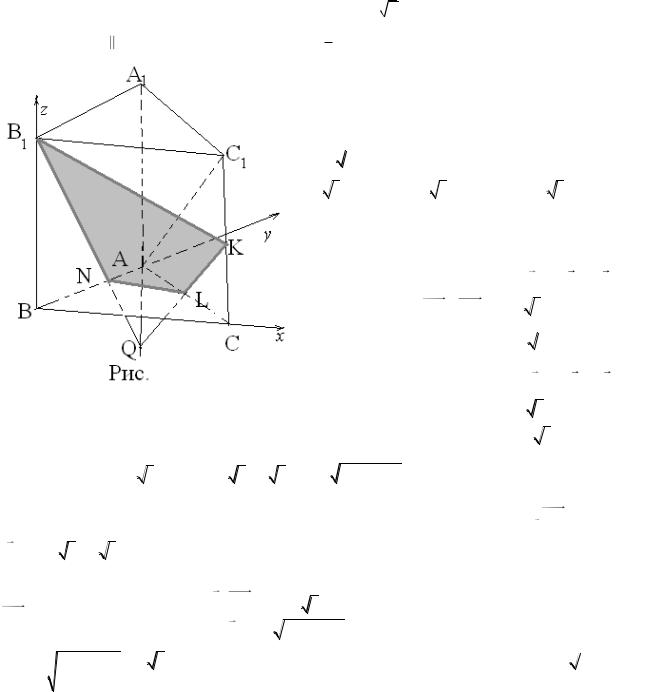
4. Основанием прямой призмы АВСА1В1С1 служит треугольник АВС с углом В, равным 90°, и углом С, равным 30°. Найдите площадь сечения призмы плоскостью, проходящей через середину бокового ребра СС1 , и вершину В и параллельной диагонали АС1 боковой грани АА1С1С, если расстояние между АС1 и секущей плоскостью равно 1/3, а гипотенуза основания призмы равна

4.

Решение.

В соответствии с условием задачи АВ=2, ВС= 23 . Построим сечение:

пл. АСС1: KL АС1 , KL АА1=Q, (AQ= 13 А1Q),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

пл. АВВ1: QB1

АВ=N, (AN=

1

AB).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

KLNB1 - искомое сечение .

 

Введем си-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

стему координат: В(0;0;0). А(0;2;0),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С(2

3 ;0;0),

 

В1 (0;0;h), А1(0;2;h),

 

 

С1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

h),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( 2 3 ;0;h),

 

 

 

L(

3 ;1;0),

 

 

 

 

 

K( 2

3 ;0;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N(0;

 

4

 

;0). Площадь сечения

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

B L NK

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

KLNB

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

1

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

SKLNB

 

 

3

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12 3 8 3h

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(5h; 15h; 20 3)

 

 

 

 

 

(h;3

3

h; 4

 

3)

 

 

 

28h2 48.

Чтобы найти h, использу-

 

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12

 

 

 

 

 

 

1

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ем условие задачи:

( AC , )

 

. С другой стороны,

( AC , )

Пр AN

, здесь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n (h;3

3h;4

3) . Точки А и N , ( A AC1, N ),

выбраны,

как наиболее удоб-

ные по координатной записи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n AN

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

AN (0;

; 0),

 

 

( AC , )

 

 

 

 

 

2 3h

 

 

 

 

 

1

h2

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

n

 

 

 

 

 

 

 

28h2 48

 

 

3

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

5

 

 

28 3

48

3 5

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

 

3 5

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12

 

 

5

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

В заключение, отметим, что в основе всех рассмотренных выше решений лежит один незатейливый алгоритм, основанный на сводке приведенных выше формул. Использование его в условиях конкурсного состязания, когда дефицит времени и эмоциональное напряжение конкурсанта, образно говоря, «тормозят» поиск индивидуальных геометрических (для каждой задачи своих) решений, по мнению авторов, дает выгодные преимущества участнику.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности