
разрешимость в радикалах
.docxРазрешимость уравнений в радикалах
Определение.
Пусть P – числовое поле,
 - число. Говорят, что
- число. Говорят, что
 выражается в радикалах над полем P
,если оно выражается через числа поля
P с помощью нахождения
корней произвольной степени и рациональных
операций суммы, произведения, деления
и разности. Другими словами,
выражается в радикалах над полем P
,если оно выражается через числа поля
P с помощью нахождения
корней произвольной степени и рациональных
операций суммы, произведения, деления
и разности. Другими словами,
 выражается в радикалах над полем P
,если существует последовательность
выражается в радикалах над полем P
,если существует последовательность
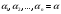 такая, что для произвольного k
такая, что для произвольного k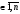 верно одно из условий:
верно одно из условий:
-
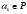 ,
, -
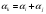 ,
или
,
или
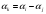 ,
или
,
или
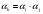 ,
или
,
или
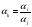 ,
где i<k,j<k;
,
где i<k,j<k; -
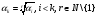 .
.
Пример.
P=Q.
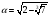 - выражается в радикалах над Q:
- выражается в радикалах над Q:
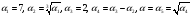 .
.
Определение.
Алгебраическое уравнение
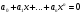 с коэффициентами из P
называется разрешимым в радикалах над
P, если все его корни
выражаются в радикалах над P.
с коэффициентами из P
называется разрешимым в радикалах над
P, если все его корни
выражаются в радикалах над P.
Определение.
Число
 выражается в квадратичных (квадратных)
радикалах над полем P,
если оно выражается через числа поля P
с помощью нахождения квадратных корней
и рациональных операций.
выражается в квадратичных (квадратных)
радикалах над полем P,
если оно выражается через числа поля P
с помощью нахождения квадратных корней
и рациональных операций.
Определение.
Алгебраическое уравнение
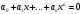 с коэффициентами из P
называется разрешимым в квадратичных
радикалах над P, если все
его корни выражаются в квадратичных
радикалах над P.
с коэффициентами из P
называется разрешимым в квадратичных
радикалах над P, если все
его корни выражаются в квадратичных
радикалах над P.
Теорема.
Пусть
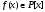 - полином, неприводимый над P,
при этом
- полином, неприводимый над P,
при этом
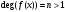 .
Если n не является степенью
двойки, то ни один из корней этого
полинома не выражаются в квадратичных
радикалах над P.
.
Если n не является степенью
двойки, то ни один из корней этого
полинома не выражаются в квадратичных
радикалах над P.
Доказательство.
От противного. Пусть
 - корень
- корень
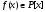 ,
который выражаются в квадратичных
радикалах над P, т.е.
существует последовательность
,
который выражаются в квадратичных
радикалах над P, т.е.
существует последовательность
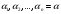 из первого определения (r=2).
из первого определения (r=2).
Построим
последовательность расширений:
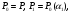
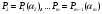 .
.
Для
любого k
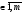 рассмотрим расширение
рассмотрим расширение
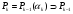 .
Если
.
Если
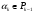 ,
то
,
то
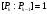 ,
если
,
если
 ,
то
,
то
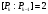 .
Таким образом,
.
Таким образом,
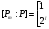 .
.
Если
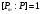 ,
то
,
то
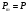 ,
тогда
,
тогда
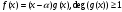 ,
т.е. полином приводим – противоречие.
,
т.е. полином приводим – противоречие.
Если
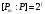 ,
то рассмотрим цепочку расширений
,
то рассмотрим цепочку расширений
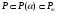 .
Данные расширения конечные. Тогда
.
Данные расширения конечные. Тогда
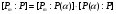 ,
т.е.
,
т.е.
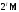 (так
как
(так
как
 - корень неприводимого полинома
- корень неприводимого полинома
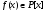 степени n), из чего следует,
что n является степенью
двойки. Противоречие. Теорема доказана.
степени n), из чего следует,
что n является степенью
двойки. Противоречие. Теорема доказана.
Следствие*.
Пусть
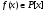 ,
,
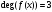 .
Уравнение
.
Уравнение
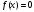 разрешимо в квадратичных радикалах над
P тогда и только тогда,
когда один из корней этого полинома
принадлежит полю P.
разрешимо в квадратичных радикалах над
P тогда и только тогда,
когда один из корней этого полинома
принадлежит полю P.
Доказательство. Самостоятельно.
Геометрические построения с помощью циркуля и линейки. Необходимое и достаточное условия разрешимости задач на построение.
Пусть задано некоторое конечное множество точек М. Тогда:
1.Если точка A принадлежит M, то точку A можно построить.
2. Если точки A и B можно построить, то прямую AB можно построить.
3. Если точки O и A можно построить, то можно построить окружность с центром в точке O радиуса OA.
4. Если можно построить пересекающиеся прямые l и m, то можно построить их точку пересечения.
5. Если можно построить прямую l и окружность O, имеющие общие точки, то можно построить любую их общую точку.
6. Если можно построить окружности O и O', имеющие общие точки, то можно построить любую их общую точку.
7. Никакие другие точки нельзя построить.
Пусть задано множество М точек плоскости, которое содержит 2 точки А и А'. Через них можно провести прямую. Пусть А-0, А’ – 1. С помощью циркуля и линейки можно построить прямую, проходящую через 0 и перпендикулярную АА’. На ней построим АB= АА’. Получим декартову систему координат.
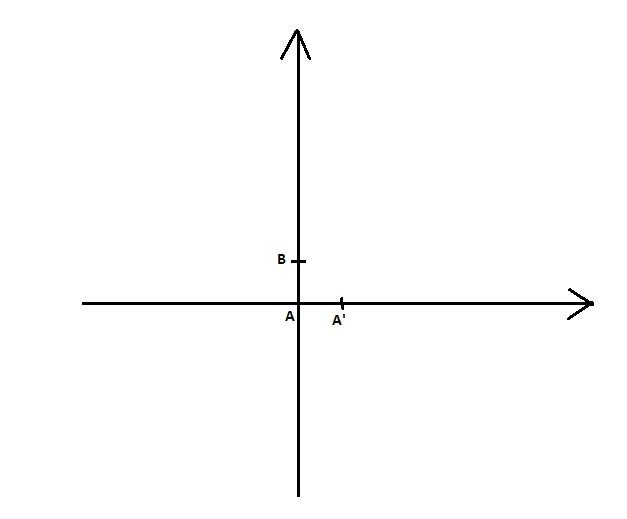
С одной стороны, точки плоскости можно отождествлять с комплексными числами.
С другой стороны, Точку М(a;b) можно рассматривать как точку плоскости R2. Построить точку М – значит построить отрезки, длины которых равны a и b.
В таком случае можно построить:
a+b,
a-b (если
a<b, то
(b-a) построим
в противоположном направлении оси),
a*b, b/a,
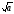 .
.
Следствие. Если построены точки a и b, то с помощью циркуля и линейки можно построить любые элементы из расширения Q(a,b).
Далее будем отождествлять плоскость с R2. Точка М(a.b) определена над полем P, если ее координаты принадлежат P.
Свойство.
Если точки A1(x1,y1),
A2(x2,y2)
определены над P, то прямую,
проходящую через них, можно записать в
виде: ax+by=c,
где
 .
.
Доказательство.
Уравнение прямой:
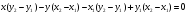 ,
причем
,
причем
 .
.
Свойство.
Если точки A1(x1,y1),
A2(x2,y2)
определены над P, то
окружность с радиусом
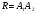 и центром в точке A1,
задается уравнением
и центром в точке A1,
задается уравнением
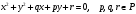 .
.
Доказательство. Аналогично.
Свойство.
Пусть заданы прямые ax+by=c
и dx+ey=f,
где
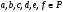 .
Координаты точки их пересечения
определены над P.
.
Координаты точки их пересечения
определены над P.
Доказательство. Аналогично(решить систему и найти координаты точки пересечения).
Свойство.
Пусть заданы прямая ax+by=c
и окружность
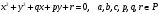 .Тогда
точка (точки) их пересечения определена
либо над P, либо над
.Тогда
точка (точки) их пересечения определена
либо над P, либо над
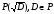 .
.
Доказательство.
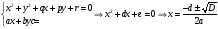 .
Если b=0, то получим
аналогичный результат.
.
Если b=0, то получим
аналогичный результат.
Свойство.
Пусть заданы две окружности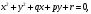
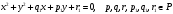 .
Тогда точка (точки) их пересечения
определена либо над P,
либо над
.
Тогда точка (точки) их пересечения
определена либо над P,
либо над
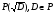 .
.
Теорема1.
Пусть М – множество точек, определенных
над P. Для того, чтобы можно
было построить с помощью циркуля и
линейки некоторые точки, необходимо и
достаточно, чтобы это число принадлежало
некоторой цепочке квадратичных расширений
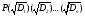 .
.
Доказательство.
Необходимость.
Пусть задано непустое множество М. Из
предыдущих свойств следует, что
построенные числа принадлежат либо P,
либо цепочке
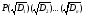 .
.
Достаточность.
Так как a и b
из P, то, по рассмотренному
ранее, a+b,
a-b, a*b,
b/a,
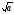 (т.е. все элементы из
(т.е. все элементы из
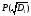 )
можно построить с помощью циркуля и
линейки. Следовательно, любой элемент
из
)
можно построить с помощью циркуля и
линейки. Следовательно, любой элемент
из
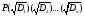 можно построить.
можно построить.
Неразрешимые задачи на построение.
Задача о квадратуре круга. Построить квадрат, равновеликий данному кругу.
Пусть радиус данного круга равен 1 (т.к.
можно взять любой масштаб).
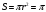 .
Площадь круга равна:
.
Площадь круга равна:
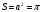 .
Таким образом, нужно построить a.
По теореме1 это можно сделать тогда и
только тогда, когда
.
Таким образом, нужно построить a.
По теореме1 это можно сделать тогда и
только тогда, когда
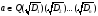 ,
т.е. конечному расширению Q,
тогда a – алгебраическое
число. Следовательно,
,
т.е. конечному расширению Q,
тогда a – алгебраическое
число. Следовательно,
 - алгебраическое. Противоречие. Таким
образом, такой квадрат построить с
помощью циркуля и линейки нельзя.
- алгебраическое. Противоречие. Таким
образом, такой квадрат построить с
помощью циркуля и линейки нельзя.
Задача о трисекции угла. Поделить произвольный угол на три равные части.
Пусть
дан угол
 .
Нужно построить угол
.
Нужно построить угол
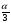 .
Построение угла эквивалентно построению
косинуса этого угла.
.
Построение угла эквивалентно построению
косинуса этого угла.
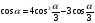 .
Пусть
.
Пусть
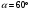 .
Тогда нужно выяснить, можно ли построить
корни данного уравнения:
.
Тогда нужно выяснить, можно ли построить
корни данного уравнения:
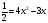 ,
так как
,
так как
 является его корнем. Имеем:
является его корнем. Имеем:
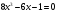 .
Уравнение не имеет рациональных корней,
значит
.
Уравнение не имеет рациональных корней,
значит
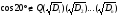 (следствие*).
Построить данный угол нельзя.
(следствие*).
Построить данный угол нельзя.
Таким образом, не любой угол можно построить с помощью циркуля и линейки. (Но некоторые можно. Например, угол 900).
Задача о делении круга на n равных частей. (построение правильного n- угольника).
Дана окружность. Вписать в нее правильный n-угольник.
См в предложенных статьях.
